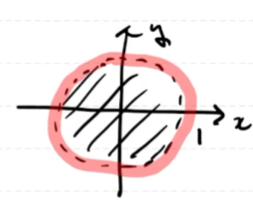
X=(x,y) 또는 X=(x,y,z)라 하자.
D⊂R2orR3
이 때, domain D는 open set이다.
예를 들어, 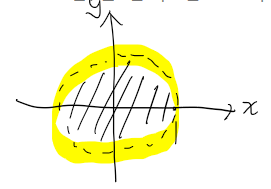
위와같은 상황일 때,
D:={(x,y)∣x2+y2<1} 이라 할 수 있고,
이 때 영역 ∂D는 ∂D:={(x,y)∣x2+y2=1}로 정의한다.
특히, Dˉ=D∪∂D
보통, 미분을 할 때 영역의 경계는 일반적으로 포함하지 않습니다.
예를 들어,
- f:[0,1]→R일 때 연속이고,
- (0,1)에서 미분 가능하다.
라는 식으로 미분 문제를 풀 수 있게끔 가정이 주어지곤 했습니다.
D⊂R을 domain이라 합시다.
이 때, C2(D)는 C2(D)라는 집합에 포함되는 변수는 모두 이계도함수가 잘 정의 된다는 뜻입니다.
예를 들어, u∈C2(D)라면, uxx,uxy,uyx,uyy가 모두 존재하며, 특히 연속입니다.
즉, 2계도함수가 연속이기 때문에 당연히 u, ux,uy가 모두 연속일 거라는 결론이 도출됩니다.
이 때, 특별한 언급이 없으면 우선 uxy=uyx라 가정합니다.
Theorhm(Vanishing Theorhm)
f가continousinDˉ,whereDisboundeddomain, f≥0inDˉ 이면,
∭Df(X)dx=0
⇒f≡0inDˉ
즉, 음이 아닌 함수 값을 적분했을 때 0이 나오면, 그 함수 값 자체도 0이 된다.
또한,
D0:∀D⊂D0inR2orR3일 때,
∭Df(x)dx=0이면
⇒f≡0inD0
proof
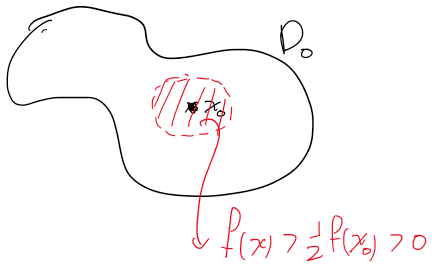
만약, 특정 point x0에서 함수 값이 0이 아니라 하자(f(x0)=0).
그러면, f(x0)>21f(x0)을 만족하는 이웃을 찾을 수 있을 것이다. 그러면, 해당 영역에서는 적분 값이 0이 될 수 없기 때문에 모순이다.
Theorhm(Chain Rule)
(s.t)→(x,y)→u
x=g(s,t)
y=h(s,t)
이 때, u를 s,t에 대한 함수로 이해할 수 있고, 아래와 같이 연쇄법칙(Chain rule)을 적용할 수 있다.
- ∂s∂u=∂x∂u∂s∂x+∂y∂u∂s∂y
- ∂t∂u=∂x∂u∂t∂x+∂y∂u∂t∂y
Excercise
극좌표 u(x,y)를 x=rcosθ,y=rsinθ로 이해할 수 있다.
이 때, 아래와 같은 식이 성립한다.
uxx+uyy=urr+r1ur+r21uθθ
Proof
ur
=∂r∂u
=∂x∂u∂r∂x+∂y∂u∂r∂y
...
urr
=∂r∂(ur)
...
Hint : ∂r∂u에서 u대신 ux를 대입하면 ∂r∂(ux)를 구할 수 있다(아니면 그냥 일계도함수에 연쇄법칙을 한 번 더 적용할 수 있다).
이후는 그냥 굿노트에 적자. 시간이 너무 많이 든다ㅎㅎ..