[수학이론] Partial Difference Equation(편미분 방정식)

본 시리즈는 W.A., Strauss, Partial Differential Equations: An Introduction, 2nd Edition를 기반으로 하는 편미분방정식 개념에 관한 내용을 포함합니다.

Definition (PDE)

Partial Difference Equations(PDEs), 즉 편미분방정식은 변수가 2개 이상인 unknown function(보통 $u$)과 그 함수($u$)의 편미분으로 이루어진 방정식이다.

이 때, 변수가 1개라면 Ordinary differential equations, 즉 상미분방정식이라 합니다.

보통 독립변수는 $x,y,z,t$ 등이 등장한다. 여기서 $t$는 시간에 대한 변수로 여기고, 나머지를 단순 변수로 여기는 경향이 있다. 여기서는 보통

Example

소개 할 예시들은 모두 아래의 조건을 가정으로 한다.

1. $u=u(x,t)$
2. $u_t={{\partial u}\over{\partial t}}, u_x={{\partial u}\over{\partial x}}$
3. $t: time, t>0$

(1) $u_t+u_x=0$ (transport equation)

(2) $u_t=u_{xx}$ (heat equation in one dimension)
(3) $u_t=u_{xx}+u_{yy}$ (heat equation in two dimension)

• 위의 두 식(2,3)은 heat equation(열 방정식) 대신 diffusion equation(확산 방정식)으로 표현할 수도 있다.
• 이 때, 차원은 $t$를 제외한 나머지 독립변수($x, y$ 등)의 개수에 해당한다.

(4) $u_{tt}=u_{xx}$ (wave equation in one dimension)

• wave equation은 파동 방정식이라 하는데, 파동과 관련된 식인 만큼 $sin, cos$ 함수가 포함된 해가 도출된다.

(5) $u_{xx}+u_{yy}=0$ (Laplaces's equation)

이 방정식의 관점에서는 라플라스 방정식이라고 하지만, 솔루션인 $u$의 관점에서는 harmonic function, 즉 조화함수라고 한다.

왜 위 식의 $u$를 조화함수라 할까?
$u_t=u_{xx}+u_{yy}+u_{zz}$가 성립한다 가정하면, $u=u(x,y,z)$는 3차원 heat equation이 된다.
만약, 3차원의 밀폐된 방이 있다 가정하자.
이 때, 한 모서리의 점에서 불을 피운다고 가정했을 때, 3차원 공간 내 특정 좌표 $x_0, y_0, z_0$에서의 시간 $t_0$일 때의 온도의 변화량을 $u_t|_{t_0}$이라 할 때 $u_{t}|_{t_0}=u_{xx}|_{x_0}+u_{yy}|_{y_0}+u_{zz}|_{z_0}$를 만족한다.
시간이 많이 지난다면, 공간 내의 열평향 상태가 되므로 위 식의 $u_t=0$을 만족하게 된다. 그렇다면 위의 3d heat equation $u_t=u_{xx}+u_{yy}+u_{zz}$는 $0=u_{xx}+u_{yy}+u_{zz}$, 즉 3차원의 라플라스 방정식이 된다. 이는 평형을 이루는 상태기 때문에 harmonic하다 하는 것.

즉, 라플라스 방정식과 열 방정식은 유사한 방정식이라 할 수 있다.
당연하게도 유사한 방정식끼리 유사한 해법을 갖는다.

Definition (Order)

방정식(PDE)의 order는 미분이 제일 많이 되어 있는 수이다.

Example

$x^{2}u_t+u^{3}u_{xx}=tan(t+x^{4})$

1. 편미분이 한 번이라도 있고, 등호가 존재하므로 PDE
2. $u=u(x,t)$로 표현 가능

이 때, 미분이 가장 많이 된 항은 $u_{xx}$으로, 2번 편미분되었다. 즉, 위 식에서 order=2.

$\mathbb{R}^2$에서 first-order PDE는 아래와 같이 표현할 수도 있다.

$F(x,y,u,u_x,u_y)=0$

또한, 유사하게 일반적인 second-order PDE는 아래 같이 표현할 수 있다.

$F(x,y,u,u_x,u_y, u_{xx}, u_{xy}, u_{yy})=0$

또한, 위의 독립 인자들이 모두 들어갈 필요는 없고, 적어도 편미분이 된 항이 1개만이라도 들어가면 된다.

위 방정식의 해는 $u$이기 때문에, $u$를 중점으로 바라보면 됩니다.

Definition (Solution)

PDF의 solution(해)은 최소한 변수 $x, y, ...$의 적당한 영역에서 PDE를 만족하는 function(함수)이다.

즉, 단순히 특정 함수를 식에 대입했을 때 식이 성립하면 됩니다.
또한, 함수가 성립하기 위해서는 독립변수의 특정 점에서 함수가 정의되어야 하며, 미분(편미분)을 위해 특정 점 주위의 영역에서 함수가 정의되어야 하므로 "적당한 영역"이라는 표현이 필요합니다.

Definition (Operator)

operator $\mathcal{L}$ 는 함수를 함수로 보내는 mapping(사상)이다($T : V \rightarrow V$ ).

만약, $\mathcal{L}$이 도메인 내 모든 함수 $u,v$와 모든 복소상수 $c$에 대해 아래 식을 만족시킨다면 operator $\mathcal{L}$은 linear, 즉 선형적이라 한다.

• $\mathcal{L}(cu+v)=c\mathcal{L}u+\mathcal{L}v$

Definition (Linearity)

$\mathcal{L}$이 선형적이라 가정하자. 그러면 아래의 방정식

$\mathcal{L}u=g \ \ \cdots \ \ (1)$

는 $g=0$일 때 homoneneous linear euqation이라하고,
$g\ne 0$일 때 inhomogeneous linear equation이라 한다.

---

Remark(Superposition principle)

만약 $u_1, ..., u_n$이 homogeneous linear euqation(1) 이라면 임의의 선형 결합

$c_1u_1+\cdots +c_nu_n=\sum^{n}_{i=1}c_iu_i$

또한 해가 된다.

---

Example

1. $(cos xy^{2})u_x-y^{2}u_y=tan(x^{2}+y^{3})$

• 1st order
• linear
• homogeneous

$\mathcal{L}u=cos(xy^{2})u_x-y^{2}u_y$라 가정하자.
$\mathcal{L}(cu+v)$
$=(cosxy^{2})(cu+v)_x-y^{2}(cu+v)_y$
$=c(cosxy^{2})u_x-cy^{2}u_y+(cosxy^{2})v_x-y^{2}v_y$
$=c\mathcal{L}u+\mathcal{L}v$

2. $u_t+uu_x+u_{xxx}=0$

• 3rd order
• non linear
• inhomogeneous

$u$와 관련된 항만을 왼쪽으로 몰았을 때, 우변이 0이 되기 때문에 homogeneous이며 좌변을 $\mathcal{L}(u)$로 정의했을 때 $\mathcal{L}(2u)\ne 2\mathcal{L}(u)$이기 때문에 nonlinear이다.

3. $u_x+xu_{xy}+1=0$

• 2nd-order
• linear($u$기준)
• inhomogeneous

이 때, $\mathcal{L}=u_w+xu_{xy}$라 정의할 수 있습니다.
$\mathcal{L}=u_w+xu_{xy}=-1$ 이 성립합니다.

보다시피, $u=u(x,y)$와 같은 벡터 꼴로 이루어졌기 때문에 $x,y$는
linear를 판정하는 데 중요하지 않다.

일반적으로,
$\mathcal{F}(x,y,u,u_x,u_y)=0$ 꼴의 1st order pde라 할 때,
$a(x,y)u+b(x,y)u_x+c(x,y)u_y=g(x,y)$의 꼴만이 보통 linear라 할 수 있다.

여전히 위의 $a,b,c$는 상수가 아닌 변수입니다. 그저 linear를 판단할 때 상수로 여길 뿐입니다.

---

Notation

또한, 본 책에서는 특별한 언급이 없는 한 $u_{xy}=u_{yx}$이 성립한다 가정한다. 또한 모든 미분이 존재하며 연속적이라 가정한다.

---

Rewind

1st-order PDE는 $F(x,y,u,u_x,u_y)=0$ 꼴로 표현할 수 있다.

이 때, $\mathcal{L}(u)=\mathcal{F}(x,y)$을 만족시키게 식을 잡아보자.

즉, $u$와 관련된 term을 좌변에 몰 수 있을 때

• $\mathcal{L}(w+v)=\mathcal{L}(w)+\mathcal{L}(v)$
• $\mathcal{L}(k,w)=k\mathcal{L}(w)$

식이 성립해야 linear하다 할 수 있다.
하지만, 위와 같은 성질은 제곱항, 세제곱항 $cos, sin$ 등의 term이 있을 때는 성립할 수 없다(확인해보자)

특히, 위에서 $\mathcal{L}=0$일 때는 homogeneous라 한다.

---

Exercise

아래의 PDEs를 풀어보자(즉, unknwon func. $u$를 구해보자)..

(1) $u_x=0$

이 때, $x$에 대해 편적분을 수행하면 $u(x,y)=C+g(y)$가 성립한다.
하지만, 보통 $y$에 대한 함수에도 상수 $C$가 포함되어있다고 볼 수 있기 때문에
$u(x,y)=f(y)$ 를 해로 쓸 수 있다.

(2) $u_{xx}=0$

sol

양 변을 $x$로 편적분하면,
$u_x=f(y)$
한 번 더 하면,
$u=f(y)x+g(y)$ $\blacksquare$

Rewind (2계 선형 미분방정식의 특성방정식)

2계 선형 미분방정식의 특성방정식 $y''+by'+cy=0$에 대해 특성방정식 $r^2+br+c=0$의 해가
서로 다른 두 실근을 가지면 특성방정식의 해 $r_1,r_2$에 대해 미분방정식의 해는
$C_1e^{r_1t}+C_2e^{r_2 t}$

중근을 가지면 특성방정식의 해 $r_1$에 대해 미분방정식의 해는
$C_1e^{r_1t}+C_2te^{r_1t}$

허근을 가지면 특성방정식의 두 해 $\alpha+\beta i, \alpha-\beta i$에 대해 미분방정식의 해는
$C_1e^{\alpha t}cos(\beta t)+C_2e^{\alpha t}sin(\beta t)$<ㅠㄱ>
이다.

(3) $u_{xx}+u=0$

sol

위 식의 특성방정식의 해는

$r^2+1$
$r=\pm i$ 이고,

바로 위의 Rewind를 참고했을 때 해는 아래와 같다.
$u=f(y)cos(x)+g(y)sin(x) \cdots \blacksquare$

(4) $u_{xy}=0$

sol

양변을 $y$로 편적분하면,

$u_x=f(x)$
양변을 $x$로 편적분하면,
$u=F(x)+g(y) \; s.t. \;F'=f \cdots \blacksquare$

(5) $u_x+u_y=0$

sol(기하)

위의 식은
$(1,1)*(u_x,u_y)=0$
로 표현할 수 있다.

$u$는 미분 가능한 함수이고, 상수가 내적이 되어 있다.
이는, 방향도함수로 해석할 수 있고, 위의 식은
$D_{(1,1)}u=0$
이 된다.

이를 기하학적으로 해석하면, 아래와 같이 (1,1) 방향으로는 함수 값이 변하지 않는 모양(3차원일테지만)

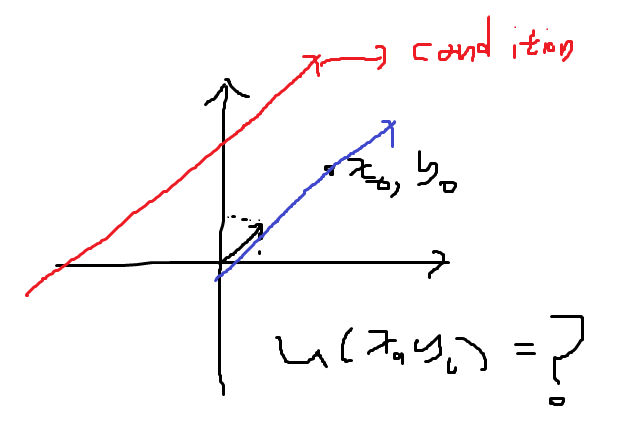
해를 푼다는 것은 $u$의 함수를 구하는 것.
이 때, initial condition이 주어져야 해가 유일하게 결정되므로, 아무 조건도 주어지지 않으면 정확한 해를 구할 수는 없다. $\cdots \blacksquare$