그리디 알고리즘 (Greedy Algorithm)

lsjoon·2024년 1월 26일

algorithm

Algorithm

목록 보기

21/22

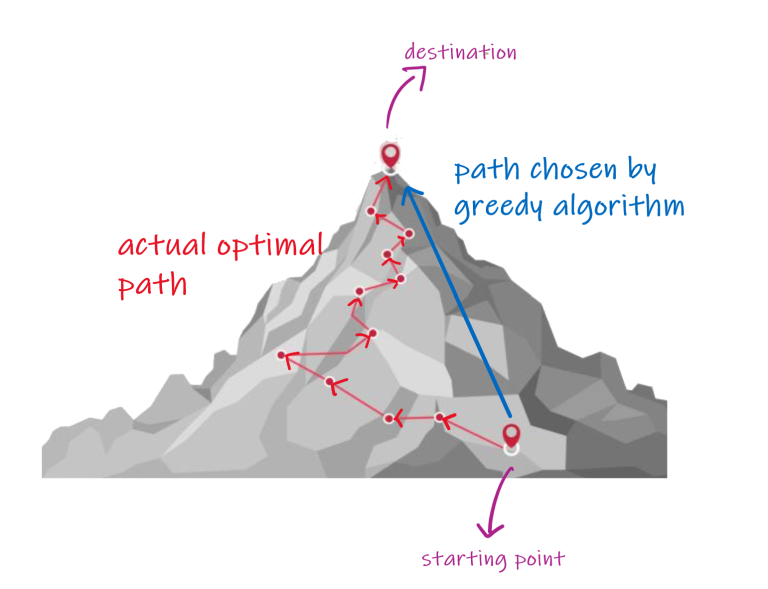
탐욕적인 방법 ( 탐욕 알고리즘 )

최적해를 구하는 데 사용되는 근사적인 방법

여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 최종 해답에 도달하는 방법

특징

- 항상 최적의 값을 보장하는 것이 아닌, 최적의 값의 "근사한 값"을 목표로 함
- 그리디 알고리즘을 적용할 수 있는 문제들은 지역적으로 최적이면서 전역적으로 최적인 문제
= 지역적으로는 최적인 선택들을 반복하여 최종적(전역적)인 해답을 도출했다고 해서 그 해답 또한 최적이라는 보장은 없음

조건

탐욕 선택 속성 (Greedy Choice Property)

앞의 선택이 이후의 선택에 영향을 주지 않음

최적 부분 구조 (Optimal Substructure)

문제에 대한 최적해가 부분문제에 대해서도 역시 최적해임

위 조건을 만족하지 않으면 그리디 알고리즘을 통해 최적해를 구할 수 없음
그러나 "근사 알고리즘"으로는 사용 가능하며, 대부분의 경우 속도가 빨라 실용적으로 사용 가능
어느 정도까지 최적해에 가까운 해를 구할 수 있는 지를 보장하기 위해서는 엄밀한 증명이 필요
그리디 알고리즘을 통해 최적해를 찾아낼 수 있는 구조 = "매트로이드"

근사 알고리즘
최적의 해를 구할 수 없는 문제에서 근사한 해를 구하는 알고리즘을 의미

활용 방법

절차

문제의 최적해 구조를 결정
선택 절차(Selection Procedure) : 문제의 구조에 맞게 선택 절차를 정의
선택 절차에 따라 선택을 수행 ( 현재 상태에서 최적인 선택을 수행 )
적절성 검사(Feasibility Check) : 선택된 해가 문제의 조건을 만족하는지 검사
조건을 만족하지 않는 해 제외
해답 검사(Solution Check) : 모든 선택이 끝난 뒤, 해답을 검사
조건을 만족하지 않으면 해답으로 인정하지 않음

Greedy VS DP

분류	Greedy Algorithm	Dynamic Programming
설명	각 단계에서 최적의 선택을 통해 문제 해결	작은 문제들을 통해 중복 계산을 피하고 큰 문제를 해결
성립 조건	1. 탐욕 선택 속성 2. 최적 부분 구조	1. 중복 부분 문제 2. 최적 부분 구조
중복 부분 문제	해결 X	해결 O
상황	각 단계의 상황에서 최적을 선택, 최적의 경로를 도출 최적의 근사값이거나, 문제를 해결하지 못할 수 있음	모든 상황을 계산하여 최적의 경로를 도출 모든 상황을 계산하기 위해 복잡도 증대

그리디로 접근 가능한 문제들

1. 거스름돈

"""
>>> input <<<
coins = [100, 10, 500, 50]
money = 1260
count = 0
"""

def change_money(coins: list, money: int, count: int) -> Dict[str, int]:
  result= {}
  # 1. 선택 절차 적용 : 거스름돈 문제에서 가장 가치가 큰 동전부터 선택을 합니다.
  coins.sort(reverse=True)

  # 2. 적절성 검사 : 만약 선택된 동전의 가치가 거스름돈보다 크다면 다음으로 작은 동전을 선택한다.
    for coin in coins:
      count += money // coin
      money %= coin
      result[str(coin)] = count

  if money == 0:
  	return result

print(change_money(coins, money, count))
  
# Output: { "500" : 2, "100" : 4, "50" : 5, "10": 6 }