다이나믹 프로그래밍 (Dynamic Programming)

lsjoon·2024년 1월 25일
algorithm

Algorithm

목록 보기
20/22

동적 계획법 (DP)

기억하며 풀기
복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법

특정 범위까지의 값을 구하기 위해 그것과 다른 범위까지의 값을 이용하여 효율적으로 값을 구하는 알고리즘 설계 기법 ( 답을 재활용하는 것 )

DP를 사용한다는 것은, 일반적인 방법에 비해 더 적은 시간 내에 해결해야 할 필요가 있어 메모리를 희생하고 속도를 높이는 것

알고리즘 기법 : 문제를 해결하기 위해 사용되는 절차적인 방법 또는 계획
- 정렬, 검색, 그래프 탐색 알고리즘 등

알고리즘 설계 기법 : ( 문제를 해결하기 위한 ) 알고리즘을 설계하는 방법이나 접근 방식
- 분할-정복, 동적 계획법, 그리디 알고리즘, 백트래킹 등

[ 활용 예시 ]
- Diff Utility ( Long Common Subsequence ) : 두 개의 파일의 차이점을 알아내기 위해 사용 ( Git 등)
- Resource Allocation ( 0-1 배낭(kanpsack) 문제 기반 )
- 연관 검색어 검색 ( Edit Distance 문제 )
- 플로이드-워셜 알고리즘 : 그래프의 모든 정점의 쌍의 최단 거리를 찾아내는 알고리즘
- 다익스트라 : 시작과 도착 사이의 양의 최단 거리를 찾아내는 알고리즘
- 벨만-포드 알고리즘 : 시작과 도착 사이의 최단 거리를 찾아내는 알고리즘

특징

- 메모이제이션 (Memoization)

중복 계산을 방지하기 위해 이전 계산 값을 캐시 후 다시 필요할 때 해당 값을 재사용

  • 시간 복잡도는 좋아지지만 공간 복잡도는 나빠질 수 있음
    = 계산 과정이 단축되지만, 답을 저장해두기 위한 추가 메모리가 필요

조건

  1. 중복되는 부분 문제 (Overlapping Subproblems)

문제를 나누고 그 문제의 결과 값을 재활용하여 전체 답을 구함
( 동일한 작은 문제들이 반복하여 나타날 경우에 사용 가능 )

  1. 최적 부분 구조(Optimal Substructure)

부분 문제의 최적 결과값을 사용해 전체 문제의 최적 결과를 낼 수 있는 경우 사용

활용 방법

절차

무차별 대입 방식보다 다이내믹 프로그래밍 솔루션이 더 빠르기 때문에 풀이 방법에 대한 다이나믹한(동적인) 사고 필요

  1. 다이나믹 프로그래밍임을 식별
    주어진 문제가 다이나믹 프로그래밍으로 해결될 수 있는 지 식별
    식별 방법은 위의 “DP에 해당되는 조건”을 찾아내는 것
  2. 매개 변수를 결정
    궁극적으로 문제 해결을 하기 위해 어떤 것이 매개 변수가 될 지 결정
    피보나치 수열의 경우 'n'
  3. 매개 변수를 부분 문제와 연결
    매개 변수를 다른 문제와 연결짓는 과정을 통해 최적화된 부분 구조를 설계
    7번째 피보나치 항은 n=7이므로
    fibo(n = 7) = fibo(n = 6) + fibo(n = 5) 로 정리 가능
  4. 문제 코딩
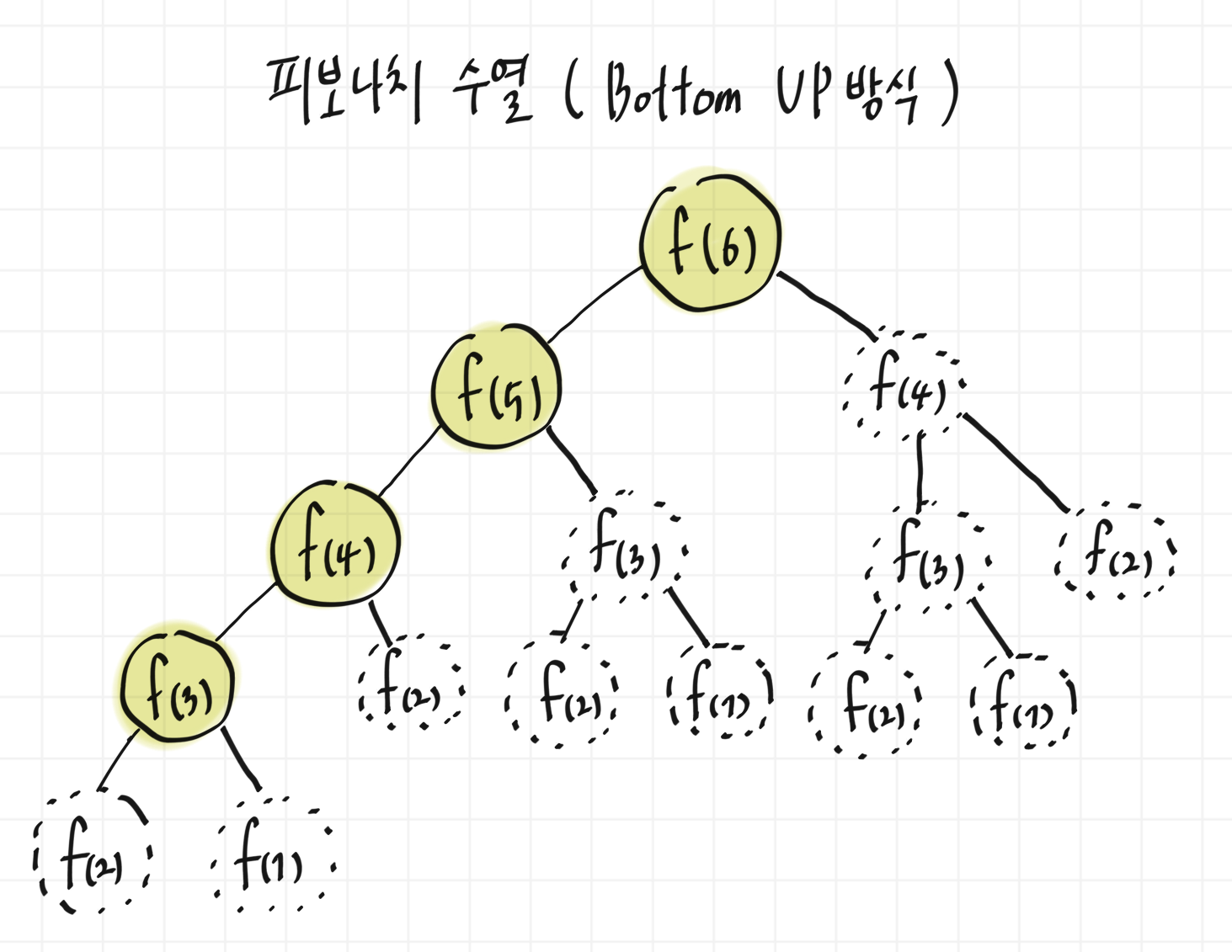
    상향식(Bottom-up), 하향식(Top-Down) 접근 중 한 가지를 선택

기본 요소

  1. 메모하기
    변수 값에 대한 결과를 저장할 배열 등을 미리 만들고 결과값이 도출될 때 마다 배열에 저장 후 재사용

  2. 변수 간 관계식 ( 점화식 ) 만들기

문제 해결 방식

  1. Bottom-Up ( Tabulation )
    [ 반복문 ]
    작은 부분 문제부터 차례대로 해결하여 전체 문제를 해결
    반복문을 통해 부분 문제들을 반복 해결하고 결과를 배열 등에 저장
  • 일반적으로 더 직관적이고 이해하기 쉬움.
  • 모든 작은 부분 문제들을 해결하기에 최적 부분 구조를 보장

  1. Top-Down ( Memoization )
    [ 재귀 ]
    큰 문제를 작은 부분 문제로 나누어 해결
    재귀 함수를 통해 문제를 쪼갬과 동시에 계산값을 Memoization 하고, 캐싱을 통해 Memo 해둔 값을 큰 문제에서 불러와 사용
  • Memoization 은 재귀를 사용하므로 구현이 더 간단할 수 있음
  • 필요한 부분 문제만 해결함으로써 시간 복잡도 개선
  • 재귀 호출의 오버헤드가 발생할 가능성 있음
  • 모든 작은 부분 문제를 해결하지 않을 경우, 최적 부분 구조를 보장하지 않을 수 있음

DP로 접근 가능한 문제들

필요조건

- 특정 데이터 내 최대화 / 최소화 계산
- 특정 조건 내 데이터 수 구하기
- 확률

1. 피보나치 수열 (Fibonacci Sequence)

- Top-Down

피보나치는 이전 두 항의 합으로 이루어지는 수열
동적 계획법을 통해 피보나치 수열을 산출

# - - - - - - - - - - - - - - - - Top_Down - - - - - - - - - - - - - - - - #
n = int(input())
dp = [ 0 for _ in range(n - 1) ]

def fibonacci(n):
  result = 0
  
  if n <= 2:
    return 1
  
  else:
    i = n - 2
    if dp[i] != 0:
      result = dp[i]
    else:
      dp[i] = fibonacci(n-2) + fibonacci(n-1)
      result = dp[i]
  
  return result
  
print(fibonacci(n))


# - - - - - - - - - - - - - - - - Bottom_Up - - - - - - - - - - - - - - - - #
n = int(input())
dp = [0] * (n + 1)
dp[0] = 0
dp[1] = 1

for i in range(2, n+1):
  dp[i] = dp[i-2] + dp[i-1]

print(dp[n])


# - - - - - - - - - - - - - - - - Bottom_Up2 - - - - - - - - - - - - - - - - #
a,b = 0,1
for _ in range(int(input()) - 1):
  a, b = b, a+b
    
print(b)

2. 배낭 문제 (Knapsack Problem)

- Bottom-UP

주어진 가방의 용량에 최대한 가치가 높은 물건을 넣는 문제
동적 계획법을 통해 가방의 용량에 따른 최대 가치를 산출

"""
>>> input <<<
아이템의 무게와 가치, 배낭의 용량
weights = [2, 3, 4, 5]
values = [3, 4, 5, 6]
capacity = 7
"""

def knapsack(weights: list, values: list, capacity: int) -> int:
  n = len(weights)
  
  ## Memoization = 2차원 배열 초기화
  dp = [0] * (n + 1)
  for i in range(n):
    dp[i] = [0] * (capacity + 1)

  ## 점화식
  for i in range(n):
    for j in range(capacity +1):
      if weight[i -1] > j:
        # 현재 아이템을 배낭에 넣을 수 없는 경우 
        dp[i][j] = dp[i -1][j]
      
      else:
        # 현재 아이템을 배낭에 넣을 수 있는 경우
        dp[i][j] = max(dp[i - 1][j], dp[i -1][j - weights[i - 1]] + values[i - 1])

  return dp[n][capacity]
  
print(knapsack(weights, values, capacity))
# Output: 9

3. 최장 증가 부분 수열 ( Longest Increasing Subsequence)

- Bottom-UP

주어진 수열에서 순서를 유지하며 가장 긴 부분 수열을 찾는 문제
동적 계획법을 통해 각 원소를 마지막으로 하는 부분 수열을 저장, 이를 이용해 전체 최장 증가 부분 수열의 길이를 산출

"""
>>> input <<<
nums = [10, 9, 2, 5, 3, 7, 101, 18]
"""
def LIS(nums: list) -> int:
  n = len(nums)
  
  ## Memoization = 배열 초기화
  dp = [1] * n
  
  ## 점화식
  for i in range(n):
    for j in range(i):
      if nums[i] > nums[j]
        dp[i] = max(dp[i], dp[j] + 1)
  
  return max(dp)
  
print(LIS(nums))
# Output: 4

4. 최단 경로 문제 (Shortest Path Problem)

- Bottom-UP

= 플로이드-워셜 알고리즘
주어진 그래프에서 시작 노드부터 도착 노드까지 최단 경로를 찾는 문제
동적 계획법을 통해 각 노드간의 거리를 바로 가는 것과 다른 노드를 경유해서 가는 방법을 비교해가며 최단거리 표를 갱신

"""
>>> input <<<
graph = [
  [0, 4, 2, 0],
  [4, 0, 1, 5],
  [2, 1, 0, 8],
  [0, 5, 8, 0]
]
start = 0
end = 3
"""

def shortestPath(graph: list, start: int, end: int) -> int:
  
  ## Memoization = 배열 초기화
  INF = float('1e9')
  n = len(graph)
  dp = [INF] * n
  
  ## 점화식
  for i in range(start, end):
    for j in range(n):
      if graph[i][j] != 0 && dp[i] + graph[i][j] < dp[j]:
        dp[j] = dp[i] + graph[i][j]
        
  return dp[end]
  
print(shortesPath(graph, start, end))
# output: 6

5. 문자열 편집 거리 문제 (Edit Distance Problem)

- Bottom-UP

두 문자열 사이의 최소 편집 거리를 찾는 문제 ( 편집 연산 = 문자 삽입, 삭제, 대체 )
동적 계획법을 통해 각 문자열의 부분 문자열의 최소 편집 거리를 저장하고, 이를 이용해 전체 편집 거리를 산출

"""
>>> input <<<
str1 = "kitten"
str2 = "sitting"
"""

def editDistance(str1: string, str2: string) -> int:
  ## Memoization = 배열 초기화
  m = len(str1)
  n = len(str2)
  dp = [ [0] * (m + 1) for _ in range(n + 1) ]
  
  for i in range(m):
    for j in range(n):
      if i == 0:
        dp[i][j] = j
      elif j == 0:
        dp[i][j] = i
      elif str1[i - 1] == str2[j -1]:
        dp[i][j] = dp[i - 1][j - 1]
      else:
        dp[i][j] = 1 + min(dp[i + 1][j], dp[i][j - 1], dp[i - 1][j - 1])

  return dp[m][n]

print(editDistance(str1, str2))
# Output: 3

5. 최장 공통 부분 문자열 (Longest Common Substring)

- Bottom-UP

주어진 문자열에서 순서를 유지하며 가장 긴 공통 문자열 부분을 찾는 문제
동적 계획법을 통해 각 문자열들을 비교하며, 공통된 가장 긴 부분을 찾는 방법

> 그림 예시 보러 가기 <

"""
>>> input <<<
str1 = "ACAYKP"
str2 = "CAPCAK"
"""

# 가장 긴 공통부분 문자열의 길이 찾기
def LCS_length(str1: string, str2: string) -> int:
  n = len(str1)
  m = len(str2)

  dp = [ [0] * (m + 1) for _ in range(n + 1) ]

  for i in range(1, n + 1):
      for j in range(1, m + 1):	
        # 삼항연산자 사용 전
        if str[i - 1] == str2[j - 1]:
          dp[i][j] = dp [i - 1][j - 1] + 1
        else:
          dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]

        # 삼항연산자 사용
        # DP[i][j] = DP[i - 1][j - 1] + 1 if str1[i-1] == str2[j-1] else max(DP[i - 1][j], DP[i][j - 1])
      
  return dp[i][j]			# max 를 한 번만 쓰면 max 값이 포함된 '배열'을 출력
  # output : 4
  
"""
>>> 'dp' graph <<<
[
  [0, 0, 0, 0, 0, 0, 0], 
  [0, 0, 1, 1, 1, 1, 1], 
  [0, 1, 1, 1, 2, 2, 2], 
  [0, 1, 2, 2, 2, 3, 3], 
  [0, 1, 2, 2, 2, 3, 3], 
  [0, 1, 2, 2, 2, 3, 4], 
  [0, 1, 2, 3, 3, 3, 4]
]
"""

# - - - - - - - - - - - - - - - 공통 문자열 출력 - - - - - - - - - - - - - - - #

def LCS(n: int, m: int, dp: list, result: list = []) -> list :
  if y < 0 or x < 0 :
    return
    
  else:  
    if DP[y][x] == DP[y-1][x] and y > 0:
      LCS(y - 1, x, result)

    elif DP[y][x] == DP[y][x-1] and x > 0:
      LCS(y, x - 1, result)

    else:
      if DP[y][x] != 0:
        result.append(str1[y-1])

      if DP[y - 1][x - 1] != 0:
        LCS(y - 1, x - 1, result)
      
      else:
      	res.reverse()			# 탑-다운으로 result 에 append 되었기 때문에 뒤집어 줌
        return result
        
  res.reverse()
  return result
  
  
res_list = LCS(n, m, dp)		# 처음에 구한 str1, str2 의 길이, LCS_length 에서 구한 dp
result = ''.join(res_list)		# LCS에서 리턴된 리스트를 문자열로 변환
print(res_list)
print(result)

"""
>>> output <<<
[ 'A', 'C', 'A', 'K' ]
ACAK
"""

사진 클릭 시 출처로 이동
출처 , 출처2, 출처3-LCS

profile
lsjoon
중요한 것은 꺾여도 그냥 하는 마음
이전 포스트

위상 정렬 (Topological Sorting)

다음 포스트

그리디 알고리즘 (Greedy Algorithm)

0개의 댓글