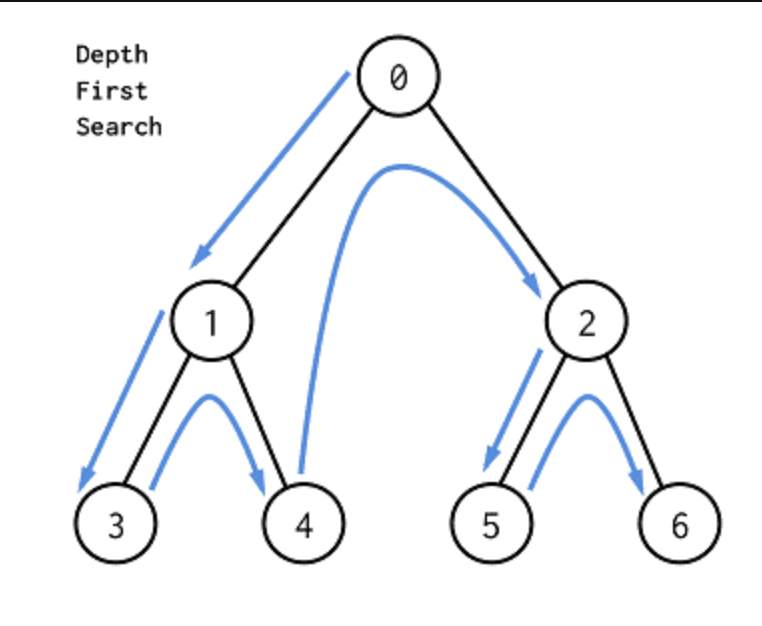
깊이우선탐색

루트 노드 ( 임의의 노드 ) 에서 시작해 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법

한 방향으로 계속 가다가 더 이상 갈 수 없게 됐을 때 가장 가까운 갈림길로 돌아와 다른 방향으로 다시 탐색을 진행

[ 활용 예시 ]
- 자동 미로 생성
- 유향 그래프의 사이클 파악

특징

- 재귀적으로 동작(재귀, 스택)
- 어떤 노드를 방문(visited)했었는지 여부를 반드시 검사 (무한루프 방지)
- 모든 노드를 방문하고자 할 때 사용

---

장단점

- 장점

• 하나의 노드에서 제일 마지막까지 탐색한 뒤 시작한 노드로 돌아오는 방식이므로 백트래킹(Backtracking)이 가능
• 찾아야하는 노드가 깊은 단계에 있을 수록, 그 노드가 좌측에 있을 수록 BFS보다 유리

- 단점

• 답이 아닌 경로가 매우 깊다면, 그 경로에 깊이 빠질 우려가 있음
• 찾은 해가 최단 경로라는 보장이 없음
• BFS 보다 간단하지만, 상대적으로 검색속도가 느림
  
  

---

복잡도

[ 노드, 간선 : V , E ]
- 인접 리스트로 표현된 그래프: O(N+E)
- 인접 행렬로 표현된 그래프: O(N^2)

---

예제

# dfs, 재귀, 인접 행렬, i 정점부터 시작
def dfs(i):
    visit[i] = True
    for j in range(1, n + 1):
        if map[i][j] == 1 and not visit[j]:
            dfs(j)

# DFS
GRAPH_SIZE = 1000

def dfs(x, v, visited):
  if visited[x]:
  	return;
  visited[x] = true;
  printf(x), end=' '
  
  for value in v[x]:
  	dfs(value, v , visited)
       
# 예시 그래프
v = [[] for _ in range(GRAPH_SIZE)]
v[1] = [2, 3]
v[2] = [1, 4, 5]
v[3] = [1]
v[4] = [2]
v[5] = [2]

visited = [False] * GRAPH_SIZE
DFS(1, v, visited)

def dfs(curr_node, graph, visited):
    visited.add(curr_node)
    for next_node in graph[curr_node]:
        if next_node not in visited:
            dfs(next_node, graph, visited)
    return visited
--------------------------------------------------------------------

def solution():
    graph = {
        'A': ['B', 'C'],
        'B': ['D', 'E'],
        'C': ['F'],
        'D': [],
        'E': ['F'],
        'F': []
    }
    
    visited = set()
    dfs('A', graph, visited)
    return visited