탐색

lsjoon·2024년 1월 16일

algorithm

Algorithm

목록 보기

12/22

완전탐색 (Brute force)

Exhaustive search
모든 경우의 수를 시도하는 방법

상대적으로 구현이 간단하고, 해가 존재하면 항상 찾게 됨
경우의 수에 따라 실행 시간이 비례하기 때문에 입력 값의 범위가 작은 경우 유용

완전탐색 알고리즘

단순 Brute-Force

반복문과 조건문을 활용해 모든 경우의 수를 구하는 방법

비트마스크 (Bitmask)

나올 수 있는 경우의 수가 각각의 원소가 '포함되거나', '포함되지 않는' 두 가지 선택으로 구성되는 경우

재귀함수

비트마스크와 마찬가지로 각 원소가 두 가지 선택지를 가질 때 유용
포함이 되면 해당 원소를 포함해 함수를 호출, 포함되지 않으면 그 상태에서 함수를 호출

시간 복잡도 = O(n)

순열 (Permutation)

서로 다른 n개를 일렬로 나열하는 방법(경우의 수)
순열의 경우의 수는 N!으로 완전탐색을 이용하기 위해서는 N이 한자리 수는 되어야 함
순열에 원소를 하나씩 채워가는 방식
재귀함수 이용
시간복잡도 = O(n!)

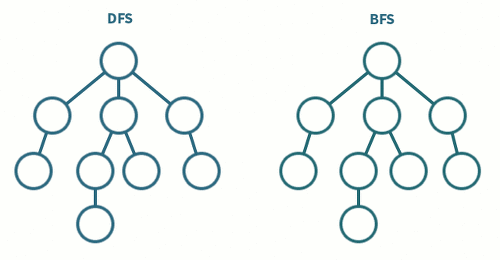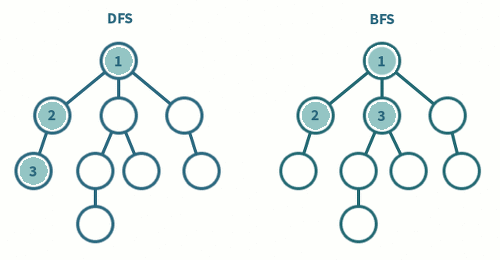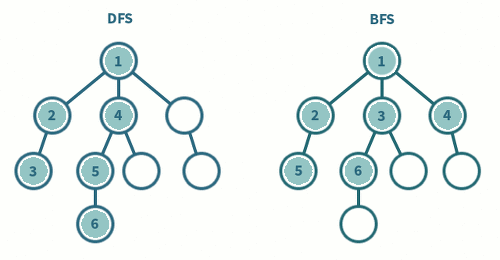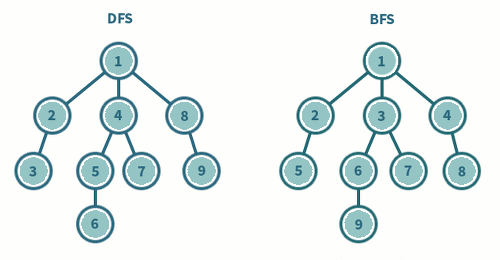
깊이우선탐색(DFS)

Depth-First Search
트리의 한 요소(노드)와 다음 수준(Level)의 자식 노드를 따라가는 방향으로 탐색
- 스택(Stack)을 활용

너비우선탐색(BFS)

Breadth-First-Search
하나의 요소를 방문하고 그 요소에 인접한 모든 요소를 우선 방문하는 형식
- 큐(Queue)를 활용

이진탐색 (Binery Search)

이분탐색
결정 문제(Decision Problem)의 답이 이분적일 때 사용할 수 있는 탐색 기법

정렬된 리스트에서 특정한 값의 위치를 찾는 알고리즘
처음 중간의 값을 임의의 값으로 선택 후, 그 값과 찾고자 하는 값의 크고 작음을 비교하는 방식

결정 문제
답은 이미 정해져 있으므로, True or False 를 찾는 문제
보통 1개의 Parameter를 가짐

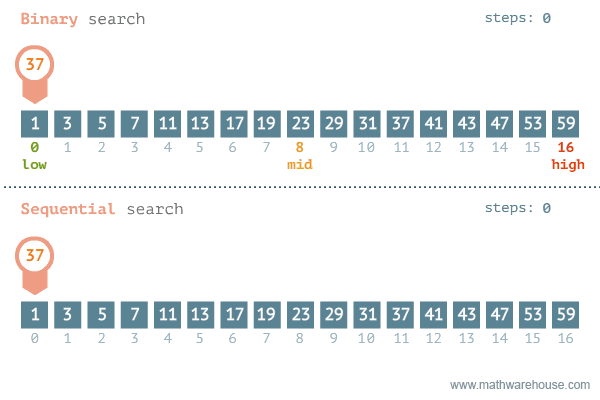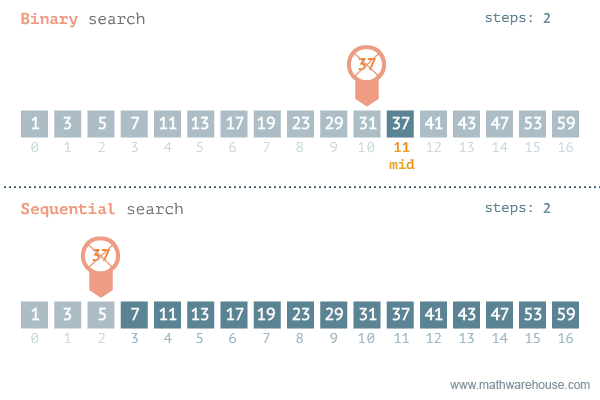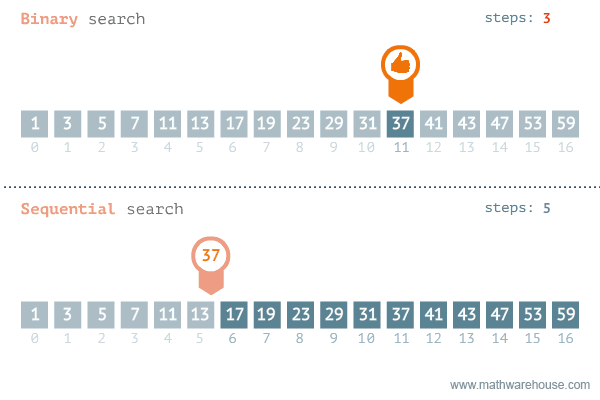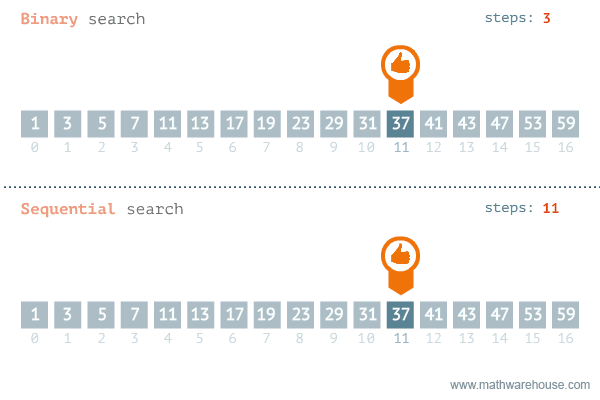
예제

N = 9
Q = None
arr = [3, 7, 9, 13, 16, 19, 23, 44, 45]

def binary_search(x):
    s, e = 0, N + 1
    
    while s + 1 < e:
        mid = (s + e) // 2
        
        if arr[mid] == x:
            return True
        elif arr[mid] < x:
            s = mid
        else:
            e = mid
            
    if arr[s] == x:
        return True
        
    return False			# while문 종료포인트

result = binary_search(9)
print(result)

# 매개 변수 탐색 (Parametric Search)

최적화 문제를 결정문제로 풀 수 있는 기법

이진탐색을 사용하여 조건을 만족하는 최대값을 찾는 방법

최적화 문제
어떤 알고리즘의 최적의 해답을 찾아내는 것

- 이진 탐색과의 차이점
이진 탐색 : 조건을 만족하는 값을 찾으면 함수를 종료
매개 변수 탐색 : 조건을 만족하는 값을 찾아도 탐색할 값이 남아있지 않을 때까지 계속 탐색

예제

def binary_search(arr,lo,hi,value):
    while lo + 1 < hi:
        mid = (lo + hi) // 2
        if arr[mid] <= value:
          lo = mid
        else:
          hi = mid
    return arr[lo]