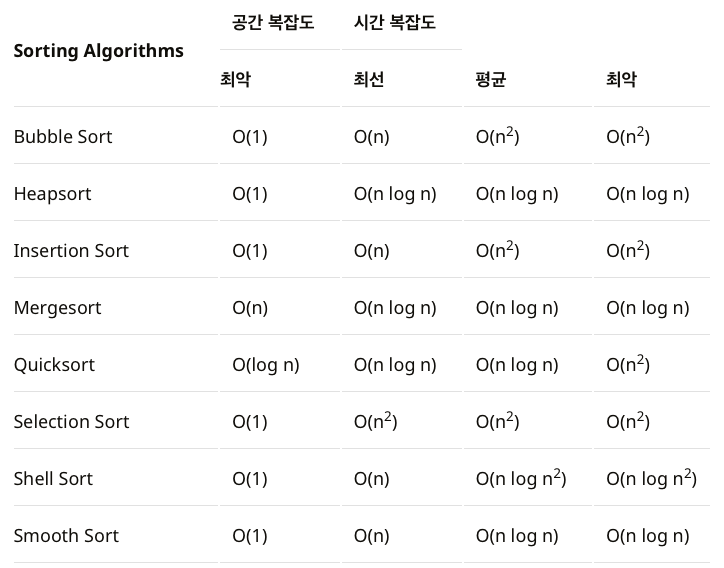
정렬 알고리즘 복잡도 비교
정렬의 종류
버블정렬 (Bubble Sort)
인접한 두 데이터 간 비교
안정 정렬 / 제자리 정렬
복잡도 : O(n^2)
정렬방식
- 첫번째와 두번째, 두번째와 세번째, ... (n-1)과 n을 비교한 뒤 위치를 교환
- 첫번째 순환이 종료 시, 가장 큰 값이 맨 뒤에 위치
선택정렬 (Selection Sort)
주어진 데이터 중 최소값을 찾아 순서대로 정렬
불안정 정렬 / 제자리 정렬
복잡도 : O(n^2)
정렬방식
- 후보군 중 최소값을 찾고, 맨 앞의 데이터와 교체
- 교체된 맨 앞의 데이터를 제외한 나머지 후보군에서 다시 최소값을 찾음
삽입정렬 (Insertcion Sort)
데이터를 하나씩 확인하면서, 각 데이터를 적절한 위치에 삽입
안정 정렬 / 제자리 정렬
복잡도 : O(n^2)
정렬방식
- 현재 선택한 데이터와 이전 위치의 데이터를 비교, 선택한 데이터가 더 작다면 위치를 교환 ( 시작 위치는 두번째 데이터 )
- 선택한 데이터보다 작은 데이터를 만날 때까지 반복, 없는 경우 첫번째에 위치
퀵정렬 (Quick Sort)
분할 정복 알고리즘(Divide and Conquer) 기반
가장 빠른 정렬 알고리즘 ( 같은 O(n log n) 중에서도 제일 빠름 )
재귀함수를 사용
불안정 정렬 / 제자리 정렬
복잡도 : O(n log n)
- 최악의 경우 복잡도가 O(n^2)
정렬방식
- 데이터에서 기준점(pivot)을 정하여 기준점보다 작다면 좌측, 크다면 우측에 정렬
- 기준점을 제외한 좌, 우 데이터를 각각 재정렬
- 위 과정을 재귀적으로 반복 ( 정렬, 분할, 정렬, 분할, ... )
병합정렬 (Merge Sort)
분할 정복 알고리즘(Divide and Conquer) 기반
재귀함수를 사용
안정 정렬
복잡도 : O(n log n)
- 추가 메모리 공간 필요 ( 데이터 병합 과정에서 새로운 데이터 생성 )
- 최악의 경우에도 복잡도가 O(n log n)
정렬방식
- 데이터의 크기가 0 또는 1이 될 때까지 n/2로 분할
- 두 개의 인접한 데이터를 정렬, 병합
- 위 과정을 재귀적으로 반복 ( 정렬, 병합, 정렬, 병합, ... )
힙정렬 (Heap Sort)
완전 이진 트리(Complete Binary Tree)의 일종 ( 우선순위 큐를 위해 만들어진 자료구조 )
최대값, 최소값을 쉽게 추출할 수 있음
불안정 정렬 / 제자리 정렬
복잡도 : O(n log n)
정렬의 특징들
안정 정렬 vs 불안정 정렬
- 안정 정렬 (Stable Sort)
임의 배열(벡터)에 중복된 값이 존재하는 경우 정렬 후에도 입력 순서와 동일하게 정렬
종류 : 버블 , 삽입 , 병합
- 불안정 정렬 (Unstable Sort)
처음 입력된 중복된 값의 순서가 정렬 후에도 유지된다는 보장이 없음
종류 : 선택 , 퀵 , 힙
제자리 정렬 (In-place Sort)
추가적인 메모리 공간을 많이 필요로 하지 않거나, 전혀 필요없는 정렬
따라서, 공간 복잡도가 O(1)
종류 : 삽입 , 선택 , 버블 , 퀵 , 힙
분할 정복 (Divide and Conquer)
큰 문제를 작은 문제로 분할하여 각각을 해결하고, 그 결과를 이용해 전체 문제를 해결
이때 분할된 작은 문제는 원래 문제와 같은 형태이며, 작은 문제는 원래 문제의 일부분이 됨
작은 문제를 재귀적으로 해결하고, 이를 결합하여 원래 문제를 해결
- Divide
분할이 가능한 문제라면, 2개 이상의 문제로 나눈다.- Conquer
나누어진 문제들이 여전히 분할이 가능하면, 다시 Divide를 수행한다.
그렇지 않으면 문제를 푼다.- Combine
Conquer한 문제들을 통합하여 원래 문제의 답을 얻는다.
종류 : 이진 탐색 , 병합 정렬 , 퀵 정렬
출처 : 사진 클릭 시 이동