B-Tree

Balanced-Tree, Bayer-Tree, BSRL-Tree

"Rudolf Bayer" 가 창시한 Self-balanced Tree 중 가장 유명한 자료구조

- 이진트리를 확장해 하나의 노드가 가질 수 있는 자식 노드의 최대 숫자가 2 보다 큰 트리
    = 노드의 개수(M)에 따라, M차 B-Tree
- 하나의 노드에 여러 개의 데이터(Key)를 저장하여 트리의 높이(Height) 을 낮춤으로써 탐색 시간을 줄이도록 고안된 트리

---

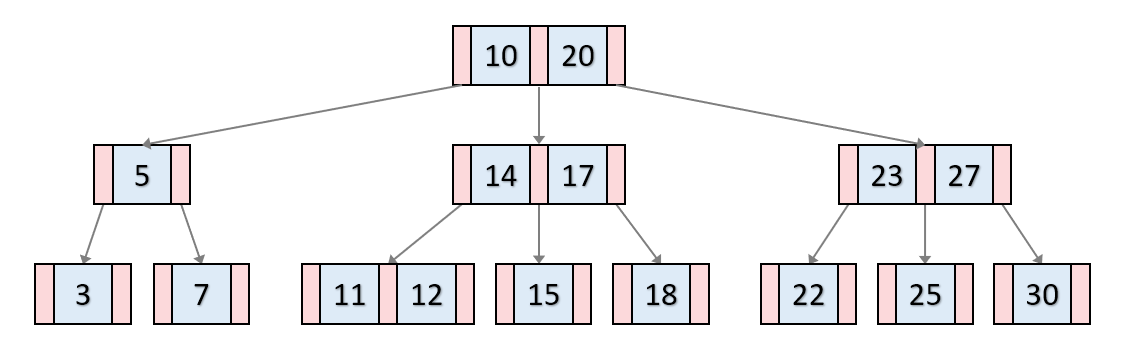
[ 3차 B-Tree ]

---

특징

1. 노드 안 Key 는 정렬되어야 함
2. 자식 노드의 Key 는 부모 노드의 Key 에 따라 배치됨
3. 모든 리프 노드의 높이(Height)는 같아야 함
4. 노드는 최대 M개의 자식 노드 보유 가능
   ( 3차 B-Tree = 최대 3개의 자식 노드 )
5. M차 B-Tree 라면, 자식 노드의 수는 최소 (M / 2)개 이상 ( 루프 노드, 리프 노드 제외 )
   ( 3차 B-Tree = 최소 2개의 자식 노드 )
6. 노드 안에 K 개의 Key가 있다면, 자식 노드의 수는 (K + 1)
7. 리프 노드의 Key 수는 최소 ({M / 2} - 1), 최대 (M - 1)
   ( 3차 B-Tree = 최소 1개, 최대 2개의 Key )

---

원리

>> 그림 예시 보기 <<

탐색 [ 하향식 ]

- 자식 노드의 Key 는 부모 노드의 Key 에 따라 오름차순으로 배치됨
- 대소비교를 통해 알맞은 브랜치를 따라 원하는 Key 를 찾을 때까지 탐색

삽입 [ 상향식 ]

- 노드에 들어있는 Key 수가 (M - 2)개 이하라면, 바로 삽입
- 삽입 후 Key 수가 M 개라면, B-Tree 조건 위배( Key 수는 최대 M-1 )로 인해 해당 Key 를 부모 노드로 올리고 자식 노드들을 새롭게 분리
  >>> 위 과정을 B-Tree 조건을 만족할 때까지 재귀적으로 수행

삭제 [ 재구조화 ]

- 삭제 시 B-Tree 의 조건 3가지 ( 특징 5, 6, 7 번 ) 를 만족하도록 트리를 재구조화(Restructuring)

1. Key 가 삭제된 노드의 나머지 Key 를 분할
2. 부모 노드로 올린 뒤 자식 노드를 B-Tree 의 조건에 맞게 재배치
3. 현재 노드와 자식 노드 모두 Key 값이 최소인 경우, 트리의 높이를 조절 ( 삭제된 Key 의 자식 노드를 합치고, 부모 노드를 내려 자식으로 연결 하는 등 )

---

B * Tree

균형을 유지하기 위한 연산에서 노드의 생성과 부가적인 연산을 최소화하기 위해 등장

• M차 B-Tree 일 때, 자식 노드 Key 의 최소량이 (M / 2)개 ( M * 2/3)개로 변경
• 노드가 가득 찼을 때, 분열하지 않고 형제 노드로 재배치

---

B + Tree

B-Tree의 확장 개념

B-Tree 와 달리 오직 리프 노드에만 Key - Value 를 저장
리프 노드끼리는 연결 리스트(Linked List)로 연결

- 장점

• 메모리 효율이 증가
• 트리의 높이 감소
• 리프 노드의 Key 만 탐색하면 되므로 탐색에 매우 유리

---

사진 클릭 시 출처로 이동
출처 , 출처2