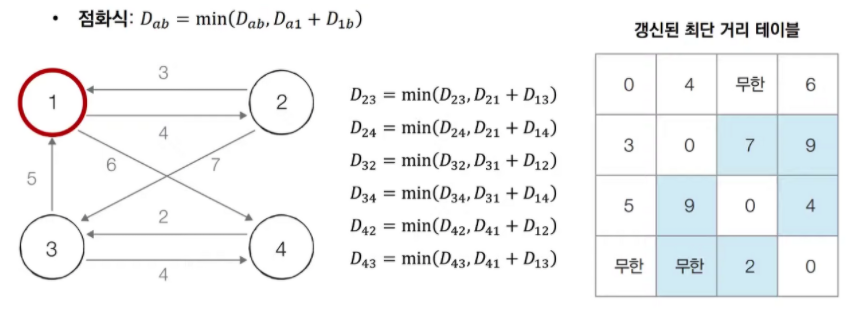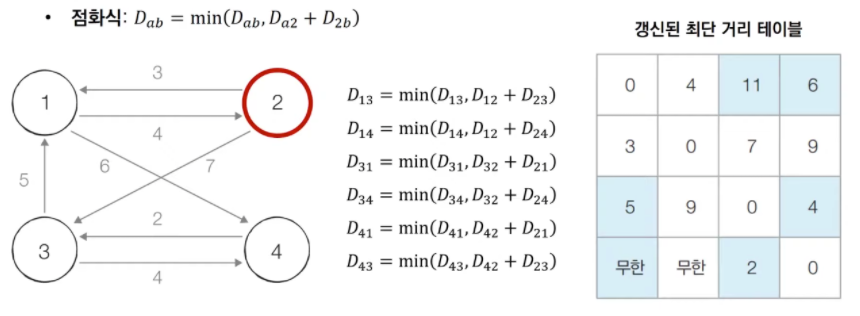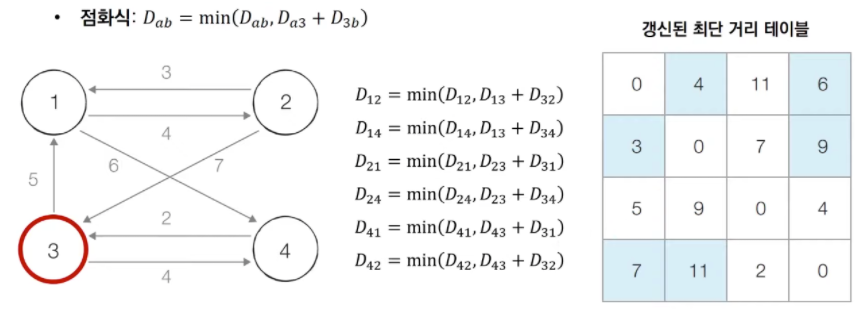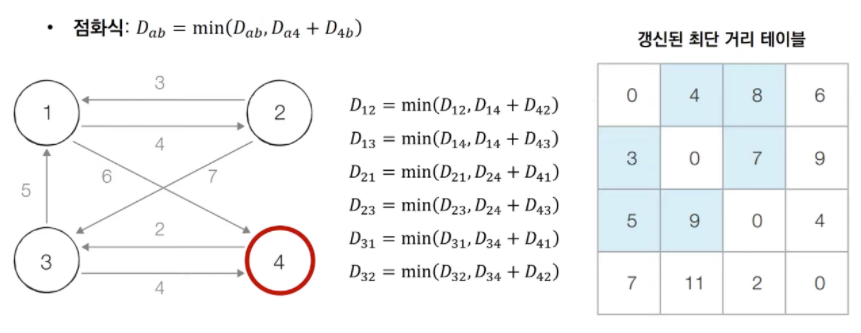플로이드-워셜 알고리즘 (Floyd-Warshall Algorithm)

가능한 모든 노드쌍들에 대한 최단거리를 구하는 알고리즘

DP(Dynamic Programming Algorithm)에 속함
- 노드의 개수가 N 개 일 때, N번 만큼의 단계를 반복하며 2차원 리스트를 갱신

복잡도 : O(N^3)

---

최단 경로 검색방법

• 가중치가 없을 때 : BFS
• 가중치가 다르고, 음수 간선이 없을 때
  - 1차원 (시작점이 하나) : 다익스트라 (Dijikstra)
  - 2차원 (시작점이 여러개) : 플로이드-워셜 (Floyd-Warshall)
• 가중치가 다르고, 음수 간선이 있을 때 : 벨만-포드 (Bellman-Ford)

너비 우선 탐색(Breadth-First Search, BFS)과의 차이
- BFS는 가중치가 없는 그래프에서 최단 경로를 찾는 알고리즘
- 좀 더 많은 정점을 지나가지만 가중치가 적은 경로가 있을 수 있음
- 가중치 그래프에서는 다익스트라 알고리즘이 가중치의 합이 작은 최단 경로를 찾는데 이용

• 다익스트라 알고리즘
  - 테이블 = 1차원 (시작점이 1개)
  - '거쳐가는 노드'를 기준으로 알고리즘 수행

• 플로이드-워셜 알고리즘
  - 테이블 = 2차원 (시작점이 n개)
  - '모든' 노드에서 모든 노드로의 최단 경로 탐색

---

원리

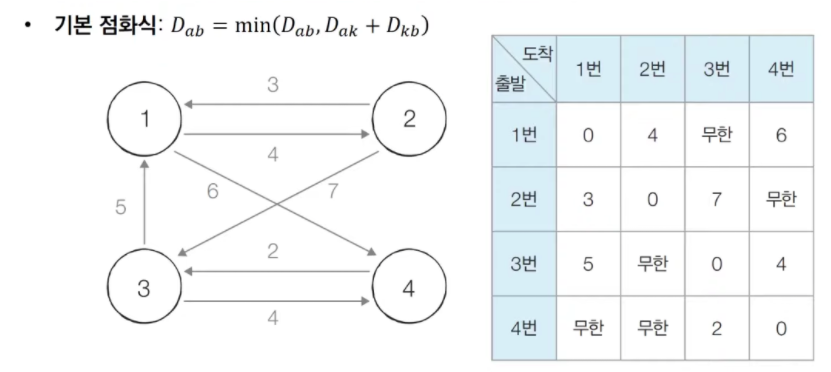
그래프의 노드와 간선에 따라 최단거리 테이블을 갱신

1번 노드를 거쳐 가는 경우를 고려하여 테이블 갱신

2번 노드를 거쳐 가는 경우를 고려하여 테이블 갱신

3, 4, .. n번 노드를 거쳐 가는 경우를 고려하여 테이블 갱신

---

예제

INF = int(1e9)

n, m = map(int, input().split())

# 2차원 리스트 생성 후 무한대로 초기화
graph = [ [INF] * (n + 1) for _ in range (n + 1) ]

# 자기 자신으로의 거리는 0으로 초기화
for i in range (1, n + 1)
	graph[i][i] =0
    
# 노드 s -> e 에 대한 가중치 w 를 입력받고 graph 초기화
for _ in range(m):
  s, e, w = map(int, input().split()
  graph[s, e] = w


# 점화식
for t in range(1, n + 1):			# 경유지
  for s in range(1, n + 1):			# 시작점
    for e in range(1, n + 1):	    # 끝점
# 정점 간 거리를 바로 가는 것과 돌아가는 것 중 더 짧은 것으로 초기화
      graph(s, e) = min(graph[s, e], graph[s, t] + graph[t, e])

# 출력
for s in range(1, n + 1):
  for e in range(1, n + 1):
    if graph[s, e] == INF:
      print('INFINITY', end=' ')
    else:
     print(graph[a][b], end=' ')
   print()

# sample input
# 4 7
# 1 2 4
# 1 4 6
# 2 1 3
# 2 3 7
# 3 1 5
# 3 4 4
# 4 3 2

---

예제 출처 , 출처