4. Trust-Region Methods

개요

Line search는 search direction을 먼저 정하고, 그에 맞는 step length를 구한다. Trust-region은 모델이 objective function을 잘 나타내는 영역을 정의한다음, 그 영역에서의 minimzer를 선택한다. direction과 step length를 동시에 정한다 볼 수 있다.

본 챕터에서는 모델 $m_{k}$가 quadratic 하다고 가정한다.

$B_{k}$는 이 때 symmetric matrix이고 $g_{k}=\nabla f(x_{k})$, $f_{k}=f(x_{k})$이다. 이는 $f$의 Taylor series expansion에 기반한 것이다.

이니 $m_{k}-f(x_{k}+p)=O(\|p\|^{2})$인 것을 볼 수있다. 각 iteration에서 다음 step은 아래의 subproblem 통해 얻을 수 있다.

이 때, $\Delta_{k}>0$이 trust-region의 radius이다. Constraint이 $p^{T}p\leq \Delta^{2}_{k}$로 나타내어질 수도 있으니 objective와 constraint이 모두 quadratic하다. $B_{k}$가 positive definite이고 $\|B_{k}^{-1}g_{k}\|\leq \Delta_{k}$면 이 subproblem은 쉽게 $p^{B}_{k}=-B^{-1}_{k} g_{k}$ (full step이라고 부름)로 풀린다. 그 외의 경우는 다른 방법을 사용해야한다.

Trust-region radius를 정하기 위해 actual reduction(아래 식의 분자)과 predicted reduction(아래 식의 분모) 사이의 ratio $\rho_{k}$를 사용한다.

$p_{k}$는 $p=0$을 포함한 region에서 $m_{k}$가 minimize되도록 구했을테니, predicted reduction은 non-negative일 것이다.

1. 만약 $\rho_{k}$가 negative라면 $f(x_{k}+p_{k})>f(x_{k})$이니 step을 reject한다. 더 작은 $\Delta_{k}$를 시도해본다.
2. 만약 $\rho_{k}$가 1에 가까우면 $m_{k}$가 $f$를 잘 모델링 하는 것이니 trust region의 크기를 키워본다.
3. 만약 $\rho_{k}$가 positive지만 값이 1보다 많이 작으면, 그 값을 그대로 사용한다.

이 때, $p_{k}$를 얻기 위해서는 subproblem을 풀어야하는데 다음의 theorem을 이용한다.

Theorem 4.1

Vector $p^{\ast}$가 trust-region problem

$\lim_{p\in\mathbb{R}^{n}}m(p)=f+g^{T}p+\frac{1}{2}p^{T}Bp \quad \text{s.t.} \quad \|p\|\leq \Delta$

의 global solution이다는 다음과 동치이다. $p^{\ast}$가 feasible하고 다음의 세 조건을 만족하는 scalar $\lambda\geq0$이 존재한다.

1. $(B+\lambda I)p^{\ast}=-g$
2. $\lambda(\Delta-\|p^{\ast}\|)=0$
3. $B+\lambda I$가 positive semidefinite

Theorem 4.1의 두번째 조건으로 인해 $\| p^{\ast}\|<\Delta$인 경우(strictly inside) $\lambda=0$이어야 하고 따라서 $Bp^{\ast}=-g$, $B$는 positive semidefinite이 된다. $\|p^{\ast}\|=\Delta$인 경우 $\lambda$는 positive value를 가질 수 있다. 따라서 첫번째 조건으로 인해

이다. 따라서, $\lambda>0$일 때는 $p^{\ast}$가 $m$의 negative gradient에 colinear하다($m$의 contour에 normal).

Algorithms based on the Cauchy point

Line search에서 꽤 loose한 조건만 만족하는 step length면 globally converge하는 것을 보장할 수 있었듯, trust region에서도 subproblem의 최적해 대신 sufficient reduction하는 approximation $p_{k}$만으로도 globally converge한다. Sufficient reduction을 정량화하기 위해 Cauchy point $p^{c}_{k}$라는 개념을 도입한다. $p^{c}_{k}$는 다음과 같은 과정을 통해 구할 수 있다.

위 두 문제를 풀고 나면 $p^{c}_{k}=\tau_{k}p^{s}_{k}$이다. 개념적으로는, 먼저 linear model 버전의 (Talyor expansion의 order 얘기, $m_{k}$는 quadratic이다.) 문제를 풀고 step length $\tau_{k}$를 정한다. 이 두 문제의 solution은 closed-form으로 나타낼 수 있다. 먼저

$\tau_{k}$의 경우는 case를 나누어 생각해야하는데, $g^{T}_{k}B_{k}g_{k}\leq0$인 경우에는 $m_{k}(\tau p^{s}_{k})$가 monotonically decrease 하기 때문에 $\tau_{k}$는 trust-region bound를 만족하는 가장 큰 값 ($\tau_{k}=1$)을 선택하면 된다. $g^{T}_{k}B_{k}g_{k}>0$인 경우, $m_{k}(\tau p^{s}_{k})$가 convex quadratic이니 $\|g_{k}\|^{3}/(\Delta_{k}g^{T}_{k}B_{k}g_{k})$ 또는 boundary value인 1이 된다. 즉,

이 Cauchy step $p^{c}_{k}$는 계산복잡도가 낮고, subproblem의 approximate solution이 적합한지 결정하는데 중요한 역할을 한다. Trust-region method는 step $p_{k}$에서의 decrease가 Cauchy step에서의 decrease의 특정 상수배보다 크면 globally converge 한다.

그런데 그냥 Cauchy step으로 매 iteration 업데이트하는 것은 steepest descent ($p^{s}_{k}$를 계산하는 데 linear model 버전의 문제를 품)와 같고 rate of convergence가 느릴 수 있다. $B_{k}$를 step length 뿐 아니라 direction을 계산하는데도 사용해야 (또, $B_{k}$가 curvature를 잘 approximate해야) 빠르게 converge 할 수 있다. 따라서 주로, $B_{k}$가 positive definite 할 때마다 $p^{B}_{k}=-B^{-1}_{k}g_{k}$ (이 때, $\|p^{B}_{k}\|\leq \Delta_{k}$)을 선택한다.

주의: 이후로 k 인덱스를 생략하고, 최적해가 trust region radius $\Delta$에 따라 결정된다는 것을 강조하기 위해 $p^{\ast}(\Delta)$로 표기한다.

Dogleg method

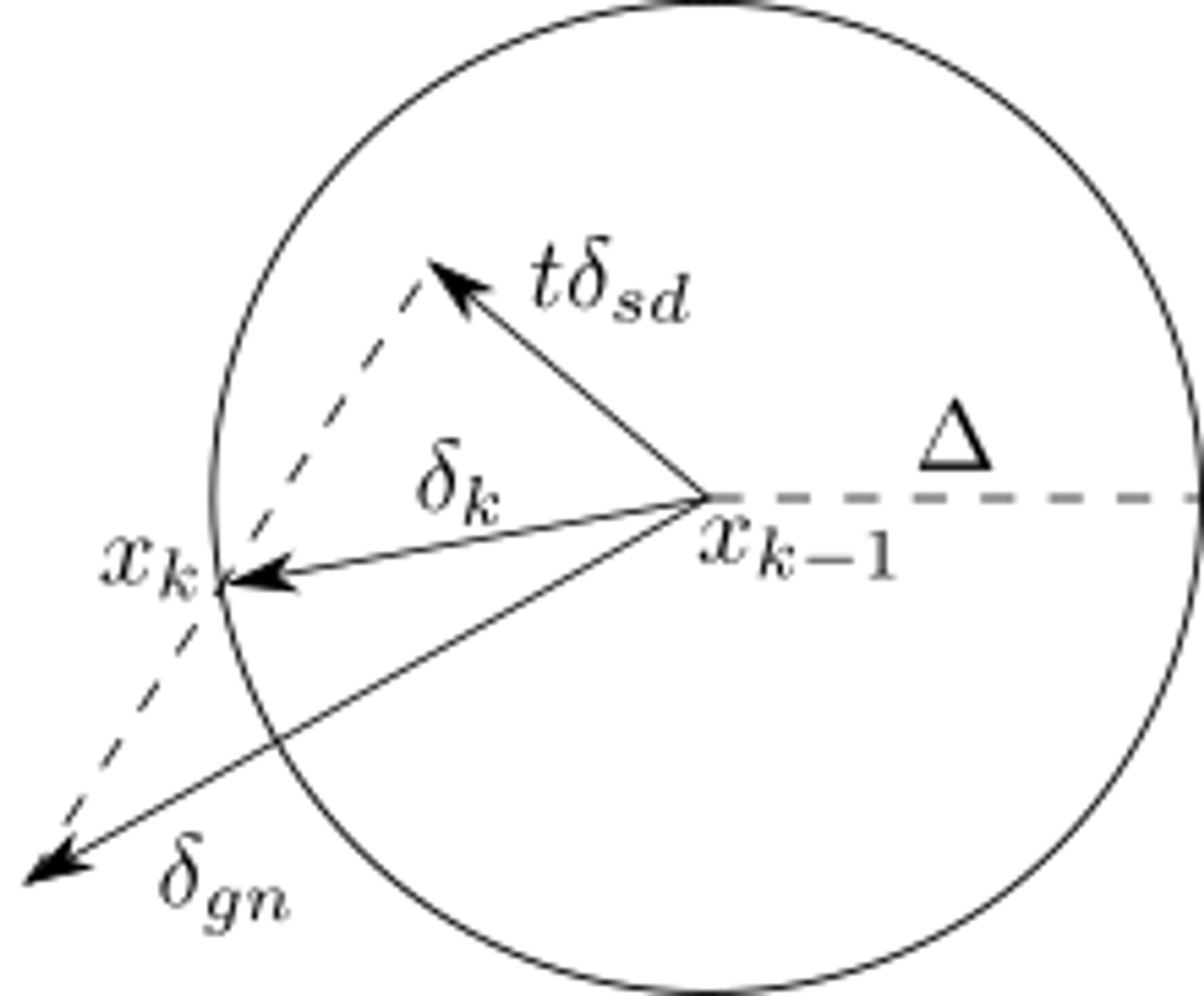
$B$가 positive definite하면 $p^{B}=-B^{-1}g$ 이다. $\Delta\geq \|p^{B}\|$면 $p^{\ast}(\Delta)=p^{B}$이고, $\Delta$가 작을 때는 model function의 quadratic term을 없애고 $p^{\ast}(\Delta)\approx -\Delta \frac{g}{\|g\|}$로 쓸 수 있다. $\Delta$가 너무 작지도 않은 값일 때는 일반적으로 아래 그림의 곡선처럼 궤도를 따른다.

Wikipedia 설명: 각 iteration에서 만약 Gauss-Newton 알고리즘의 step이 trust region 안에 있으면 이를 선택한다. 아닐 경우, Cauchy point를 구한다. Cauchy point가 trust region의 바깥에 있으면 boundary에서 truncate해서 사용한다. Cauchy point가 trust region의 안에 있으면, Cauchy point와 Gauss-Newton을 잇는 선분과 trust-region의 교차점을 선택한다. 이게 책의 설명보다 조금 더 직관적인 것 같다.

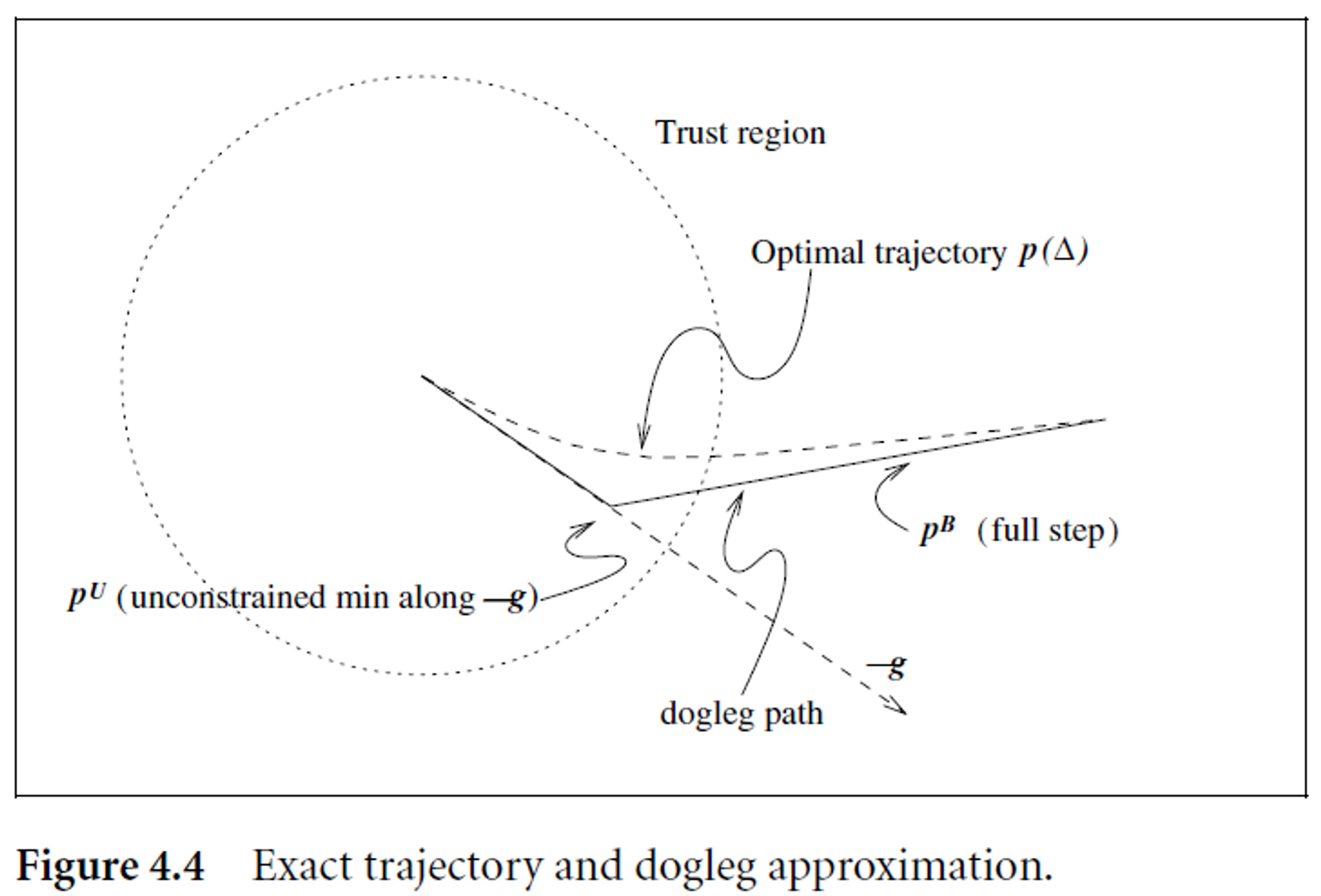
Dogleg method는 곡선 궤도를 두 line으로 approximation 한다. 첫번째 line은 origin에서 steepest descent 방향의 $m$의 minimzer이다.

두번째 라인은 $p^{U}$에서 $p^{B}$방향이다. 그러면 trajectory $\tilde{p}(\tau)$ ($\tau\in[0,2]$)는

Lemma 4.2

$B$가 positive definite이면

1. $\|\tilde{p}(\tau)\|$는 $\tau$에 대한 increasing function이다.
2. $m(\tilde{p}(\tau))$는 $\tau$에 대한 decreasing function이다.

• 증명

  $\tau\in[0,1]$에 대해서는 자명하다. $\tau\in[1,2]$을 가정하자. $h(\alpha)$를 다음과 같이 정의한다.

  $h(\alpha)=\frac{1}{2}\|\tilde{p}(1+\alpha)\|^{2}\\=\frac{1}{2}\|p^{U}+\alpha(p^{B}-p^{U})\|^{2}\\=\frac{1}{2}\|p^{U}\|+\alpha(p^{U})^{T}(p^{B}-p^{U})+\frac{1}{2}\alpha^{2}\|p^{B}-p^{U}\|^{2}$

  이를 미분하면,

  $h'(\alpha)=-(p^{U})^{T}(p^{U}-p^{B})+\alpha\|p^{U}-p^{B}\|^{2}\\ \geq -(p^{U})^{T}(p^{U}-p^{B}) \\ =\frac{g^{T}g}{g^{T}Bg}g^{T}\left(-\frac{g^{T}g}{g^{T}Bg}g+B^{-1}g\right)\\ = g^{T}g\frac{g^{T}B^{-1}g}{g^{T}Bg}\left[1- \frac{(g^{T}g)^{2}}{(g^{T}Bg)(g^{T}B^{-1}g)}g \right] \\ \geq0$

  따라서 $\|\tilde{p}(\tau)\|$는 $\tau$에 대한 increasing function이다. 또 $\hat{h}(\alpha)=m(\tilde{p}(1+\alpha))$로 정의하고, 이를 미분하면

  $\hat{h}'(\alpha)=(p^{B}-p^{U})^{T}(g+Bp^{U})+\alpha(p^{B}-p^{U})^{T}B(p^{B}-p^{U})\\\leq (p^{B}-p^{U})^{T}(g+Bp^{U}+B(p^{B}-p^{U})) \\ = (p^{B}-p^{U})^{T}(g+Bp^{B})=0$

따라서 $\|p^{B}\|\geq \Delta$이면, $\tilde{p}(\Delta)$는 trust region boundary와 딱 한군데서만 intersect한다. $m$이 decreasing function이므로, $\|p^{B}\|\leq\Delta$일 때는 $p$는 $p^{B}$이고, 그 외에는 dogleg과 trust region boundary의 intersection이다. 이 때, $\tau$는 $\|p^{U}+(\tau-1)(p^{B}-p^{U})\|^{2}=\Delta^{2}$를 풀어서 구한다.

Dogleg method는 $B$가 positive definite 할 때 적용하기 좋고, Hessian modification이 필요한 경우라면 다른 method를 사용하는 것이 낫다.

Two-dimensional subspace minimization

$B$가 positive definite일 때, dogleg method 처럼 $p$를 line에서 찾지 않고, $p^{U}$와 $p^{B}$이 span하는 공간에서 찾도록 개선할 수 있다.

이를 $B$가 indefinite할 경우에 사용하기 위해 수정할 수 있다. 즉, $B$가 negative eigenvalues를 가지면 subspace를 $\text{span}[g,(B+\alpha I)^{-1}g]$ (이 때, $\alpha\in(-\lambda_{1},-2\lambda_{1}]$, $\lambda_{1}$은 가장 작은 eigenvalue)로 바꾼다.

Global convergence

Reduction obtained by the Cauchy point

먼저 Cauchy point를 통해 얻어지는 global convergence에 대해 분석하고, 이를 위에서 다룬 method에 적용한다. Dogleg이나 two-dimensional subspace minimization 알고리즘은 다음을 만족하는 근사해 $p_{k}$를 구한다. $c_{1}\in(0,1]$에 대해,

먼저 Cauchy point $p^{C}_{k}$가 (4.20) 조건을 $c_{1}=1/2$로 만족함을 보이자.

Lemma 4.3

Cauchy point $p^{C}_{k}$에 대해

$m_{k}(0)-m_{k}(p^{C}_{k})\geq \frac{1}{2}\|g_{k}\|\min \left(\Delta_{k}, \frac{\|g_{k}\|}{\|B_{k}\|} \right)$

• 증명

  1. $g_{k}^{T}B_{k}g_{k}\leq0$인 경우,

     $m_{k}(p^{C}_{k})-m_{k}(0)=m_{k}(-\Delta g_{k}/\|g_{k}\|)-f \\=-\frac{\Delta_{k}}{\|g_{k}\|}\|g_{k}\|^{2}+\frac{1}{2}\frac{\Delta^{2}_{k}}{\|g_{k}\|^{2}}g_{k}^{T}B_{k}g_{k}\\\leq-\Delta_{k}\|g_{k}\|\\\leq -\|g_{k}\|\min \left( \Delta_{k},\frac{\|g_{k}\|}{\|B_{k}\|} \right)$

  2. $g_{k}^{T}B_{k}g_{k}>0$인 경우,
     a. $\|g_{k}\|^{3}/(\Delta_{k} g_{k}^{T}B_{k}g_{k})\leq1$인 경우,

     $\tau_{k} =\|g_{k}\|^{3}/(\Delta_{k}g^{T}_{k}B_{k}g_{k})$ (Cauchy point 계산하는 부분 참조) 이므로

     $m_{k}(p^{C}_{k})-m_{k}(0)=-\frac{\|g_{k}\|^{4}}{ g_{k}^{T}B_{k}g_{k}}+\frac{1}{2}g^{T}_{k}B_{k}g_{k}\frac{\|g_{k}\|^{4}}{(g_{k}^{T}B_{k}g_{k})^{2}}\\=-\frac{1}{2}\frac{\|g_{k}\|^{4}}{g_{k}^{T}B_{k}g_{k}}\\\leq -\frac{1}{2}\frac{\|g_{k}\|^{4}}{\|B_{k}\|\|g_{k}\|^{2}}=-\frac{1}{2}\frac{\|g_{k}\|^{2}}{\|B_{k}\|}\\\leq -\frac{1}{2}\|g_{k}\|\min(\Delta_{k},\frac{\|g_{k}\|}{\|B_{k}\|})$

     b. $\|g_{k}\|^{3}/(\Delta g_{k}^{T}B_{k}g_{k})>1$ 인 경우,

     위 식을 다시 쓰면 $g^{T}_{k}B_{k}g_{k}<\|g_{k}\|^{3}/\Delta_{k}$ 이다. 이 때 $\tau_{k}=1$이고,

     $m_{k}(p^{C}_{k})-m_{k}(0)=-\frac{\Delta_{k}}{\|g_{k}\|}\|g_{k}\|^{2}+\frac{1}{2}\frac{\Delta_{k}^{2}}{\|g_{k}\|^{2}}g_{k}^{T}B_{k}g_{k}\\ \leq -\Delta_{k}\|g_{k}\|+\frac{1}{2}\frac{\Delta_{k}^{2}}{\|g_{k}\|^{2}}\frac{\|g_{k}\|^{3}}{\Delta_{k}} = -\frac{1}{2}\Delta_{k}\|g_{k}\| \\\leq -\frac{1}{2}\|g_{k}\|\min(\Delta_{k},\frac{\|g_{k}\|}{\|B_{k}\|})$

이제 $p_{k}$가 최소한 Cauchy point로 얻어지는 reduction의 $c_{2}$배 만큼의 reduction을 달성하면 (4.20) 조건을 만족함을 보이자.

Lemma 4.4

$p_{k}$를 $\|p_{k}\|\leq \Delta_{k}$, $m_{k}(0)-m_{k}(p_{k})\geq c_{2}(m_{k}(0)-m_{k}(p^{C}_{k}))$ 을 만족하는 임의의 vector라고 하자. 그러면, $p_{k}$는 $c_{1}=c_{2}/2$로 (4.20) 조건을 만족한다. 특히 $p_{k}$가 exact solution $p^{\ast}_{k}$면 (4.20) 조건을 $c_{1}=1/2$로 만족한다.

• 증명
  $m_{k}(0)-m_{k}(p_{k})\geq c_{2}(m_{k}(0)-m_{k}(p^{C}_{k})) \\ \geq \frac{1}{2}c_{2}\|g_{k}\|\min \left(\Delta_{k}, \frac{\|g_{k}\|}{\|B_{k}\|} \right)$

Dogleg, two-dimensional subspace minimization 모두 exact solution을 approximate하며 $m_{k}(p_{k})\leq m_{k}(p^{C}_{k})$이므로 (4.20) 조건을 $c_{1}=1/2$로 만족한다.

Convergence to stationary points

$B_{k}$의 norm이 uniformly bounded 되어있고, $f$를 level set

로 정의한다. 또, 이 set의 open neigborhood를 다음과 같이 정의한다. $R_{0}>0$에 대해

결론이 더 일반적으로 적용되도록 approximate solution $p_{k}$의 길이가 trust-region bound를 넘을 수 있도록 허용하자. 구체적으로, $\gamma\geq 1$에 대해

먼저 $\eta=0$ (알고리즘 4.1 참조, 이 경우 $f$값이 낮아지기만 한다면($\rho \geq0$이면) 항상 그 step 을 취한다.)에 대해 논의하자.

Theorem 4.5

알고리즘 4.1에서 $\eta=0$을 가정하자. $\|B_{k}\|\leq \beta$, $f$는 level set에 의해 아래로 bound 되어있고, neighborhood $S(R_{0})$에서 Lipschitz continuously differentiable하다. 그리고 모든 approximate solution이 (4.20)과 (4.25) 조건을 만족한다고 가정하자. 그러면

$\liminf_{k\rarr \infty}\|g_{k}\|=0$

• 증명

  $\rho_{k}$에 약간의 조작을 가하면

  $|\rho_{k}-1|=\left| \frac{(f(x_{k})-f(x_{k}+p_{k}))-(m_{k}(0)-m_{k}(p_{k}))}{m_{k}(0)-m_{k}(p_{k})} \right| \\ = \left| \frac{m_{k}(p_{k})-f(x_{k}+p_{k})}{m_{k}(0)-m_{k}(p_{k})} \right|$

  $f(x_{k}+p_{k})$에 Taylor’s theorem을 적용하면

  $|m_{k}(p_{k})-f(x_{k}+p_{k})|=\left| \frac{1}{2}p^{T}_{k}B_{k}p_{k}-\int^{1}_{0}[g(x_{k}+tp_{k})-g(x_{k})]^{T}p_{k}dt \right| \\ \leq (\beta/2)\|p_{k}\|^{2}+\beta_{1}\|p_{k}\|^{2}$

  여기서 $\beta_{1}$은 $g$의 $S(R_{0})$에서의 Lipshcitz constant이다. 또한 $x_{k}$와 $x_{k}+tp_{k}$ 둘 다 $S(R_{0})$에 있도록 $\|p_{k}\|\leq R_{0}$을 가정했다. 여기서 $\liminf_{k\rarr\infty}\|g_{k}\|\neq0$이라고 가정하자. 즉 $\epsilon>0$과 $K>0$에 대해서

  $\|g_{k}\|\geq \epsilon \quad\text{for all}\quad k\geq K \tag{4.28}$

  이 때, (4.20)을 생각해보면, $k\geq K$에 대해,

  $m_{k}(0)-m_{k}(p_{k})\geq c_{1}\|g_{k}\|\min\left(\Delta, \frac{\|g_{k}\|}{\|B_{k}\|}\right)\geq c_{1}\epsilon\min\left( \Delta_{k},\frac{\epsilon}{\beta}\right)$

  처음 $|\rho_{k}-1|$의 식에 분모, 분자에 관한 논의를 각각 했으니 이를 조합하면

  $|\rho_{k}-1|\leq\frac{\gamma^{2}\Delta^{2}_{k}(\beta/2+\beta_{1})}{c_{1}\epsilon \min(\Delta_{k},\epsilon/\beta)}$

  이 때, 충분히 작은 $\Delta_{k}$에 대해서 위 식의 오른쪽 term이 bound 됨을 보이자. 구체적으로, $\Delta_{k}\leq \bar{\Delta}$을 만족하는 $\Delta_{k}$에 대해 얘기하자.

  $\bar{\Delta}=\min\left(\frac{1}{2}\frac{c_{1}\epsilon}{\gamma^{2}(\beta/2+\beta_{1})},\frac{R_{0}}{\gamma}\right)$

  이 때, $R_{0}/\gamma$가 들어간 이유는 $\|p_{k}\|\leq\gamma\Delta_{k}\leq\gamma\bar{\Delta}\leq R_{0}$ 이 성립하기 위함이다. $c_{1}\leq 1$이고 $\gamma\geq1$, $\beta_{1}\geq0$이므로 $\bar{\Delta}\leq \epsilon/\beta$이다. 따라서, $\min(\Delta_{k},\epsilon/\beta)=\Delta_{k}$가 성립한다. 이 사실들을 다시 적용하면

  $|\rho_{k}-1|\leq\frac{\gamma^{2}\Delta_{k}(\beta/2+\beta_{1})}{c_{1}\epsilon}\leq \frac{\gamma^{2}\bar{\Delta}(\beta/2+\beta_{1})}{c_{1}\epsilon}\leq \frac{1}{2}$

  따라서 $\rho_{k}>\frac{1}{4}$가 된다. 알고리즘 4.1을 참조하면, $\Delta_{k}\leq\bar{\Delta}$일 때마다 trust region radius를 키운다는 말이고, radius에 reduction이 있는 경우는 $\Delta_{k}> \bar{\Delta}$ 일 때 뿐이라는 말이다. 결론을 정리하면,

  $\Delta_{k}\geq \min (\Delta_{K}, \bar{\Delta}/4) \quad \text{for all}\quad k\geq K \tag{4.32}$

  모든 $k\in \mathcal{K}$에 대해서 $\rho_{k}\geq \frac{1}{4}$를 만족하는 infinite subsequence $\mathcal{K}$가 있다고 가정하자. $k\geq K$에 대해서

  $f(x_{k})-f(x_{k+1})=f(x_{k})-f(x_{k}+p_{k})\\\geq \frac{1}{4}[m_{k}(0)-m_{k}(p_{k})]\\\geq \frac{1}{4}c_{1}\epsilon \min(\Delta_{k},\epsilon/\beta)$

  두번째 줄 부등호는 $\rho_{k}\geq\frac{1}{4}$에서, 세번째 줄 부등호는 위에 있는 중간 결과에서 성립한다. $f$는 아래로 bound 되어있으니

  $\lim_{k\in\mathcal{K},k\rarr\infty}\Delta_{k}=0$

  이는 (4.32)에 모순이다. 따라서 우리가 가정한 infinite subsequence $\mathcal{K}$는 존재할 수 없고, 모든 충분히 큰 $k$에 대해서 $\rho_{k}<\frac{1}{4}$이어야 한다. 이 경우, $\Delta_{k}$는 매 iteration마다 $\frac{1}{4}$가 곱해질 것이고, 이는 다시 $\lim_{k\rarr\infty}\Delta_{k}=0$을 의미함으로 (4.32)에 모순이다. 따라서 처음 가정했던 (4.28)이 모순이 되어서 증명이 성립한다.
  

이제 $\eta>0$ (update 조건이 좀 더 strict 한 경우)에 대해 논의하자.

Theorem 4.6

알고리즘 4.1에서 $\eta\in(0,\frac{1}{4})$을 가정하자. $\|B_{k}\|\leq \beta$, $f$는 level set에 의해 아래로 bound 되어있고, neighborhood $S(R_{0})$에서 Lipschitz continuously differentiable하다. 그리고 모든 approximate solution이 (4.20)과 (4.25) 조건을 만족한다고 가정하자. 그러면

$\lim_{k\rarr\infty}g_{k}=0$

• 증명
  $g_{m}\neq 0$인 index $m$을 생각해보자. Lipschitze constant $\beta_{1}$에 대해
  $\|g(x)-g_{m}\|\leq \beta_{1}\|x-x_{m}\|$
  $\epsilon$과 $R$을 다음을 만족하도록 정의하자.
  $\epsilon=\frac{1}{2}\|g_{m}\| \\ R=\min\left(\frac{\epsilon}{\beta_{1}}, R_{0}\right)$
  $R\leq R_{0}$이므로 ball
  $\mathcal{B}(x_{m},R)=\{ x|\|x-x_{m}\|\leq R \}$
  은 $S(R_{0})$에 포함되고, $g$의 Lipschitz continuity는 $\mathcal{B}(x_{m},R)$에서 성립한다. $x\in\mathcal{B}(x_{m},R)$에 대해
  $\|g(x)-g_{m}\|\leq \beta_{1}\|x-x_{m}\|\leq\beta_{1}R\leq\epsilon=\frac{1}{2}\|g_{m}\|$
  이므로
  $\|g(x)\|\geq \|g_{m}\|-\|g(x)-g_{m}\|\geq \frac{1}{2}\|g_{m}\|=\epsilon$
  만약에 entire sequence $\{x_{k}\}_{k\geq m}$이 ball $\mathcal{B}(x_{m},R)$안에 있다면, 모든 $k\geq m$에 대해서 $\|g_{k}\|\geq\epsilon>0$일 것이다. 그럼 theorem 4.5의 (4.28) 가정 이후의 논리 전개를 다시 한번 적용할 수 있고, 결론적으로 sequence $\{x_{k}\}_{k\geq m}$ 는 ball $\mathcal{B}(x_{m},R)$을 벗어난다. Index $l\geq m$을 $x_{l+1}$이 $x_{m}$ 후 처음으로 $\mathcal{B}(x_{m},R)$를 벗어난 것이 되도록 설정하자. 그러면 $k=m,\dots,l$에 대해서 $\|g_{k}\|\geq \epsilon$ 이므로
  $f(x_{m})-f(x_{l+1})=\sum^{l}_{k=m}\left[f(x_{k})-f(x_{k+1})\right]\\\geq \sum^{l}_{k=m,x_{k}\neq x_{k+1}}\eta\left[m_{k}(0)-m_{k}(p_{k})\right]\\ \geq\sum^{l}_{k=m,x_{k}\neq x_{k+1}}\eta c_{1} \epsilon\min\left( \Delta_{k}, \frac{\epsilon}{\beta}\right)$
  Sum 기호에 $x_{k}\neq x_{k+1}$은 step이 취해진 경우에만 더하겠다는 뜻이다. 만약에 $\Delta_{k}\leq \epsilon/\beta$이면
  $f(x_{m})-f(x_{l+1})\geq \eta c_{1}\epsilon \sum^{l}_{k=m,x_{k}\neq x_{k+1}} \Delta_{k} \geq \eta c_{1}\epsilon R= \eta c_{1} \epsilon \min\left( \frac{\epsilon}{\beta_{1}},R_{0}\right)$
  만약에 $\Delta_{k}>\epsilon/\beta$이면
  $f(x_{m})-f(x_{l+1})\geq \eta c_{1}\epsilon \frac{\epsilon}{\beta}$
  Sequence $\{f(x_{k})\}^{\infty}_{k=0}$은 decreasing 하며 아래로 bound 되어있으므로
  $f(x_{k})\darr f^{\ast}$
  이 때, $f^{\ast}>-\infty$. 따라서,
  $f(x_{m})-f^{\ast}\geq f(x_{m})-f(x_{l+1})\\\geq \eta c_{1} \epsilon \min \left( \frac{\epsilon}{\beta}, \frac{\epsilon}{\beta_{1}},R_{0} \right)\\ = \frac{1}{2}\eta c_{1}\|g_{m}\| \min \left( \frac{\|g_{m}\|}{2\beta}, \frac{\|g_{m}\|}{2\beta_{1}},R_{0} \right) >0$
  $f(x_{m})-f^{\ast}\darr 0$이므로 $g_{m}\rarr 0$이다.

Iterative solution of the subproblem

Problem의 크기가 상대로 작을 때 ($n$이 너무 크지 않을 때), $B$의 factorization을 몇번 더 하는 대신 (일반적으로 총 3회, dogleg이나 two-dimensional subspace minimization은 1회 함) subproblem의 더 좋은 approximated solution을 찾을 수 있다. Theorem 4.1에서 언급한 global solution의 성질과 단변수의 Newton’s method를 이용한다. 요약하자면,

의 solution이

을 만족하도록 만드는 $\lambda$ 값을 찾는 것이다. Theorem 4.1을 생각해보면 $\lambda=0$이 $\|p\|\leq \Delta$로 1, 3번 조건을 만족하거나, 그렇지않으면 $B+\lambda I$가 positive definite이 되는 $\lambda$에 대해

를 정의해서,

를 만족하는 $\lambda>0$의 값을 찾는다. 이 문제는 $\lambda$에 대한 one-dimensional root-finding 문제이다. 원하는 성질을 가지는 $\lambda$가 존재하는지를 보기 위해서, $B$를 EVD해 $\|p(\lambda)\|$의 성질을 공부한다. $B$는 symmetric이므로 $B=Q\Lambda Q^{T}$를 만족하는 orthogonal matrix $Q$와 diagonal matrix $\Lambda$가 존재한다. 이 때, $\Lambda = \text{diag}(\lambda_{1},\dots,\lambda_{n})$, $\lambda_{1}\leq \lambda_{2} \leq \dots \leq \lambda_{n}$은 $B$의 eigenvalue 이다. 그렇다면, $B+\lambda I = Q(\Lambda + \lambda I)Q^{T}$ 이고, $\lambda\neq \lambda_{j}$라면

이 때, $q_{j}$는 $Q$의 $j$번째 column이다. 그런데 $Q$는 orthogonal이므로

따라서 $\|p(\lambda)\|$는 구간 $(-\lambda_{1},\infty)$에서 continuous, nonincreasing function이며

이고, $q^{T}_{j}g\neq 0$이면,

따라서, $\|p(\lambda^{\ast})\|=\Delta$를 만족하는 $\lambda^{\ast}\in(-\lambda_{1},\infty)$가 존재한다 ($\|p(\lambda)\|=\Delta$를 만족하는 더 작은 $\lambda$값이 있을 수 있지만 $\lambda<-\lambda_{1}$인 경우 $B+\lambda I$가 positive definite 해야한다는 조건을 만족하지 못할것이다.).

이제 $\lambda^{\ast}$를 구하는 iterative algorithm에 대해 얘기하자. 먼저, $B$가 positive definite하고 $\|B^{-1}g\|\leq \Delta$면, $\lambda^{\ast}=0$으로 즉시 종료할 수 있다. 이 외의 경우, root-finding Newton’s method를 이용하는데, 중간과정 생략하고 결론은 다음과 같다.

$q^{T}_{1}g=0$이라면, $\lim_{\lambda \rarr \lambda_{1}}\|p(\lambda)\|\neq \infty$이고, 따라서 $\|p(\lambda)\|=\Delta$를 만족하는 $\lambda\in (-\lambda_{1},\infty)$이 존재하지 않는다. 그런데 Theorem 4.1에 의해 구간 $[-\lambda_{1},\infty)$에는 존재하니 남은 것은 $\lambda=-\lambda_{1}$밖에 없다. 이 때,

처럼 단순히 $\lambda_{j}=\lambda_{1}$인 term들을 제거하는 것으로는 충분하지 않다. $B-\lambda_{1}I$가 singular이기 때문에 $(B-\lambda_{1}I)z=0$이고 $\|z\|=1$인 vector $z$가 존재한다 ($\lambda_{1}$에 해당하는 eigenvector). 따라서, 임의의 scalar $\tau$에 대해서,

로 설정하면,

이므로, $\tau$값을 잘 골라서 $\|p(\lambda)\|=\Delta$가 되도록 할 수 있다.

Theorem 4.1 증명

먼저 Lemma 하나 증명하자.

Lemma 4.7

$B$가 symmetric matrix일 때, $m$을 아래와 같은 quadratic function이라 하자.

$m(p)=g^{T}p+\frac{1}{2}p^{T}Bp$

그러면 다음의 두 진술은 참이다.

1. $B$가 positive semidefinite하고 $g$가 $B$의 range에 있을 때, 그리고 오직 그 때만, $m$은 minimum을 달성한다. $B$가 positive semidefinite 하다면, $Bp=-g$를 만족하는 모든 $p$는 $m$의 gloabl minimizer이다.
2. $B$가 positive definite할 때, 그리고 오직 그 때만, $m$은 unique minimizer를 갖는다.

• 증명

  ‘$B$가 positive semidefinite하고 $g$가 $B$의 range에 있을 때, $m$은 minimum을 달성한다’를 증명하자. $Bp=-g$를 만족하는 $p$가 존재한다. 모든 $w\in \mathbb{R}^{n}$에 대해

  $m(p+w)=g^{T}(p+w)+\frac{1}{2}(p+w)^{T}B(p+w)\\=(g^{T}p+\frac{1}{2}p^{T}Bp)+g^{T}w+(Bp)^{T}w+\frac{1}{2}w^{T}Bw \\ = m(p)+\frac{1}{2}w^{T}Bw \geq m(p)$

  따라서 $p$는 $m$의 minimizer이다.

  역을 증명하자. $p$가 $m$의 minimizer라 하자. $\nabla m(p)=Bp+g=0$이므로 $g$는 $B$의 range에 있다. $\nabla^{2}m(p)=B$ 가 positive semidefinite하다.

  ‘$B$가 positive definite할 때, $m$은 unique minimizer를 갖는다.’를 증명하려면, 첫번째 논증에서 $w^{T}Bw>0$으로 바꾸면 된다. 역을 증명하려면, $w^{T}Bw=0$인 $w\neq0$이 존재한다고 가정하자. 그럼 $m(p+w)=m(p)$이므로 minimizer가 unique하지 않아서 모순이다.
  

Theorem 4.1의 조건들을 만족하는 $\lambda \geq 0$이 존재한다고 가정하자. Lemma 4.1의 (1)에 의해 $p^{\ast}$는 아래 quadratic function의 global minimum이다.

$\hat{m}(p)\geq \hat{m}(p^{\ast})$이므로

$\lambda(\Delta-\|p^{\ast}\|)=0$이고 따라서 $\lambda(\Delta^{2}-(p^{\ast})^{T}p^{\ast})=0$이므로,

$\lambda \geq 0$이므로, $\|p\|\leq \Delta$인 모든 $p$에 대해 $m(p)\geq m(p^{\ast})$이고 따라서 $p^{\ast}$는 global minimizer이다.

역을 증명하기 위해 $p^{\ast}$가 gloabl minimizer라고 가정하고 조건들을 만족하는 $\lambda\geq0$이 존재함을 보이자. $\|p^{\ast}\|<\Delta$일 때, $\nabla m(p^{\ast})=Bp^{\ast}+g=0$이고, $\nabla^{2}m(p^{\ast})=B$는 positive semideifinite이다. 따라서 조건은 $\lambda=0$에 대해 만족한다. $\|p^{\ast}\|=\Delta$일 때, $p^{\ast}$는 constrained problem

을 해결하는데, Lagrangian function으로 나타내면

이다. 이 Lagrangian function이 $p^{\ast}$에서 stationary point를 갖게 만드는 $\lambda$를 찾는다. $\nabla_{p} \mathcal{L}(p^{\ast},\lambda)$를 0으로 설정하면

따라서 첫번째 조건이 성립한다. $p^{T}p=(p^{\ast})^{T}p^{\ast}=\Delta^{2}$를 만족하는 $p$에 대해서 $m(p)\geq m(p^{\ast})$이므로,

여기서 $g=-(B+\lambda I)p^{\ast}$를 대입하고 정리하면,

이 때,

가 dense 하기 때문에 세번째 조건이 성립한다. 이제 $\lambda$가 non-negative 하다는 것만 보이면 된다. 만약에 negative 하다고 가정한다면, $\|p\|\geq \|p^{\ast}\|=\Delta$ 이면 $m(p)\geq m(p^{\ast})$이다. $\|p\|\leq\Delta$인 범위 내에서 $p^{\ast}$가 minimizer이기 때문에 두 사실을 합치면, $p^{\ast}$는 $m$의 global, unconstrained minimizer이다. 이 때, Lemma 4.7의 (1)에 의해, $Bp=-g$이고 $B$는 positive semidefinite이다. 따라서 조건이 $\lambda=0$으로 만족하고 negative하다는 가정에 모순이다.

Convergence of algorithms based on nearly exact solution

Algorithm 4.3을 이용해서 approximate solution을 구할 때, 일반적으로 2, 3 iteration 후 얻어진 결과를 사용하고 비교적 정확한 approximation을 구하려고 하지 않는다. 다만, Theorem 4.5와 4.6이 적용될 수 있도록 safeguard를 적용할 수 있는데 구체적으로

를 만족하도록 한다. Cauchy point의 global convergence 분석에서 나온 (4.20) 식과 달리 위의 sufficient decrease 조건은 $m$의 second-order part도 사용해서 $B$가 negative eigenvalue를 가지고 $g=0$인 경우에도 감소할 수 있게 만든다.

Global convergence를 분석하기 위해서 exact Hessian 을 사용하면 limit point에 대해 더 많은 정보를 알 수 있는데,

Theorem 4.8

Theorem 4.6의 가정을 만족하고 $f$가 level set $S$에서 twice continuously differentiable하다고 가정하자. 모든 $k$에 대해서 $B_{k}=\nabla^{2} f(x_{k})$이고 approximate solution $p_{k}$가 (4.52)를 만족한다고 가정하자. 그러면 $\lim_{k\rarr \infty}\|g_{k}\|=0$이다.

또, 만약 $S$가 compact하다면, 알고리즘은 local solution에 대한 second-order necessary condition을 만족하는 점 $x_{k}$에서 종료하거나, $\{x_{k}\}$가 그러한 조건을 만족하는 점 $x^{\ast}$로 수렴한다.

Local convergence of trust-region Newton method

Trust-region Newton method의 rate of convergence에 대해 분석하기 위해서 iteration이 진행되어 solution의 근처로 갈수록 model이 원 함수를 더 잘 모델링하고 (trust-region 내에서), 따라서 trust-region Newton method의 step이 true Newton method에 수렴한다는 것을 보인다(asymptotically similar).

Theorem 4.9

$f$가 second-order sufficient condition을 만족하는 점 $x^{\ast}$의 neighborhood에서 twice Lipschitz continuously differentiable 하고, sequence $\{x_{k}\}$가 $x^{\ast}$로 수렴하며, 충분히 큰 모든 $k$에 대해서 $B_{k}=\nabla^{2} f(x_{k})$로 설정한 trust-region algorithm이 $\|p^{N}_{k}\|\leq \frac{1}{2}\Delta_{k}$일 때마다 Cauchy-point-based model reduction criterion (4.20)을 만족하고 Newton step $p^{N}_{k}$에 asymptotically similar한 step $p_{k}$를 선택($\|p_{k}-p^{N}_{k}\|=o(\|p^{N}_{k}\|)$)한다고 가정하자.

그러면, 충분히 큰 모든 $k$에 대해서 trust-region bound $\Delta_{k}$는 inactive해지고, sequence $\{x_{k}\}$는 $x^{\ast}$로 superlinearly 수렴한다.

• 증명

  충분히 큰 모든 $k$에 대해서 $\|p^{N}_{k}\|\leq \frac{1}{2}\Delta_{k}$이고, $\|p_{k}\|\leq \Delta_{k}$이어서 iteration이 진행됨에 따라 near-optimal step이 취해질 것이라는 것을 보이자.

  먼저 충분히 큰 모든 $k$에 대해 predicted reduction $m_{k}(0)-m_{k}(p_{k})$의 lower bound를 구한다. $o(\|p^{N}_{k}\|)$가 $\|p^{N}_{k}\|$보다 작아질만큼 $k$가 크다고 가정하자. $\|p^{N}_{k}\|\leq \frac{1}{2}\Delta_{k}$이면, $\|p_{k}\|\leq \|p^{N}_{k}\|+o(\|p^{N}_{k}\|)\leq 2\|p^{N}_{k}\|$ 이고, $\|p^{N}_{k}\|>\frac{1}{2}\Delta_{k}$이면, $\|p_{k}\|\leq \Delta_{k}<2\|p^{N}_{k}\|$이다. 두 경우 모두

  $\|p_{k}\|\leq 2\|p^{N}_{k}\|\leq 2\|\nabla^{2}f(x_{k})^{-1}\|\|g_{k}\|$

  이고 따라서 $\|g_{k}\|\geq \frac{1}{2}\|p_{k}\|/\|\nabla^{2}f(x_{k})^{-1}\|$이다. (4.20)으로부터

  $m_{k}(0)-m_{k}(p_{k})\geq c_{1}\|g_{k}\|\min \left(\Delta_{k}, \frac{\|g_{k}\|}{\|\nabla^{2}f(x_{k})\|} \right) \\ \geq c_{1} \frac{\|p_{k}\|}{2\|\nabla^{2}f(x_{k})^{-1}\|}\min \left(\|p_{k}\|, \frac{\|p_{k}\|}{2\|\nabla^{2}f(x_{k})\|\|\nabla^{2}f(x_{k})^{-1}\|} \right) \\ =c_{1}\frac{\|p_{k}\|^{2}}{4\|\nabla^{2}f(x_{k})^{-1}\|^{2}\|\nabla^{2}f(x_{k})\|}$

  이다. $x_{k}\rarr x^{\ast}$이므로, 충분히 큰 모든 $k$에 대해 다음의 bound가 성립함을 보이기 위해 $\nabla^{2}f(x)$의 continuity와 $\nabla^{2}f(x^{\ast})$의 positive definite함을 이용한다.

  $\frac{c_{1}}{4\|\nabla^{2}f(x_{k})^{-1}\|^{2}\|\nabla^{2}f(x_{k})\|}\geq \frac{c_{1}}{8\|\nabla^{2}f(x^{\ast})^{-1}\|^{2}\|\nabla^{2} f(x^{\ast})\|}=c_{3}$

  이 때, $c_{3}>0$이다. 따라서 충분히 큰 모든 $k$에 대해서

  $m_{k}(0)-m_{k}(p_{k})\geq c_{3}\|p_{k}\|^{2}$

  이다. $x^{\ast}$ 주변에서 $\nabla^{2}f(x)$의 Lipschitz continuity와 Taylor’s theorem을 이용하면

  $|\left( f(x_{k})-f(x_{k}+p_{k})\right) -\left( m_{k}(0)-m_{k}(p_{k}) \right)| \\ =\left| \frac{1}{2} p^{T}_{k}\nabla^{2}f(x_{k})p_{k}-\frac{1}{2}\int^{1}_{0}p^{T}_{k}\nabla^{2}f(x_{k}+tp_{k})p_{k}dt \right| \\ \leq \frac{L}{4}\|p_{k}\|^{3}$

  이 때, $L>0$은 Lipschitz constant이다. 그러면, 충분히 큰 $k$에 대해

  $|\rho_{k}-1|\leq \frac{\|p_{k}\|^{3}(L/4)}{c_{3}\|p_{k}\|^{2}}=\frac{L}{4c_{3}}\|p_{k}\|\leq \frac{L}{4c_{3}}\Delta_{k}$

  Trust-region radius는 $\rho_{k}$가 1/4보다 클 때만 줄어들 수 있으니 sequence $\{\Delta_{k} \}$는 0으로부터 bounded away 된다. $x_{k}\rarr x^{\ast}$이므로, $\|p^{N}_{k}\|\rarr 0$이고 따라서 $\|p_{k}\|\rarr 0$이다. 따라서 trsut-region bound는 충분히 큰 모든 $k$에 대해서 inactive하고, bound $\|p^{N}_{k}\| \leq \frac{1}{2}\Delta_{k}$는 iteration이 진행됨에 따라 항상 만족할 것이다.

  Superlinear convergence를 증명하기 위해, Newton’s method의 quadratic convergence를 이용한다.

  $\|x_{k}+p^{N}_{k}-x^{\ast}\|=o(\|x_{k}-x^{\ast}\|^{2})$

  $\|p^{N}_{k}\|=O(\|x_{k}-x^{\ast}\|)$이므로

  $\|x_{k}+p_{k}-x^{\ast}\|\leq\|x_{k}+p^{N}_{k}-x^{\ast}\|+\|p^{N}_{k}-p_{k}\|\\ =o(\|x_{k}-x^{\ast}\|^{2})+o(\|p^{N}_{k}\|)=o(\|x_{k}-x^{\ast}\|)$

  따라서 superlinear하게 converge한다.
  

Theorem 3.5에 따라 충분히 큰 모든 $k$에 대해서 $p_{k}=p^{N}_{k}$라면 $\{x_{k} \}$는 $x^{\ast}$로 quadratic하게 converge한다.

Enhancements

Scaling

Poor scaling의 경우 spherical trust region 보다 elliptical이 나을 수 있다. 이는 diagonal matrix $D$에 대해서 $\|Dp\|\leq \Delta$ 로 표현할 수 있다.

Trust region in other norms

일부 상황 (문제의 크기가 너무 크다던지) 같은 경우는 Euclidean norm 대신 l1 또는 $\infty$ norm 등을 사용할 수 있다.