머신 러닝 - Logistic Regression

◾Logistic Regression

1. Logistic Regression 개념

• Logistic Regression : 분류기에 사용, 이진 분류 문제(대상이 범주형인 경우)에 사용
  • 회귀 모델이 아닌 분류 모델로 로지스틱 회귀는 이진 및 선형 분류 문제에 대한 간단하고 효율적인 방법
  • 악성 종양을 찾는 경우
    • $h_{\theta}(x)=\theta_{0}+\theta_{1}x$, x : 종양의 크기
    • $h_{\theta}(x)$가 0.5보다 크거나 같으면 1(악성)으로 예측
    • $h_{\theta}(x)$가 0.5보다 작으면 0(양성)으로 예측
    • Linear Regression으로 해결가능할 수 있지만 이상치가 있는 경우 적용하기 어려울 것이다.
  • 분류 문제에서 0 또는 1로 예측해야하는 경우 Linear Regression을 적용하면 0보다 작거나 1보다 큰 값을 가질 수 있다.
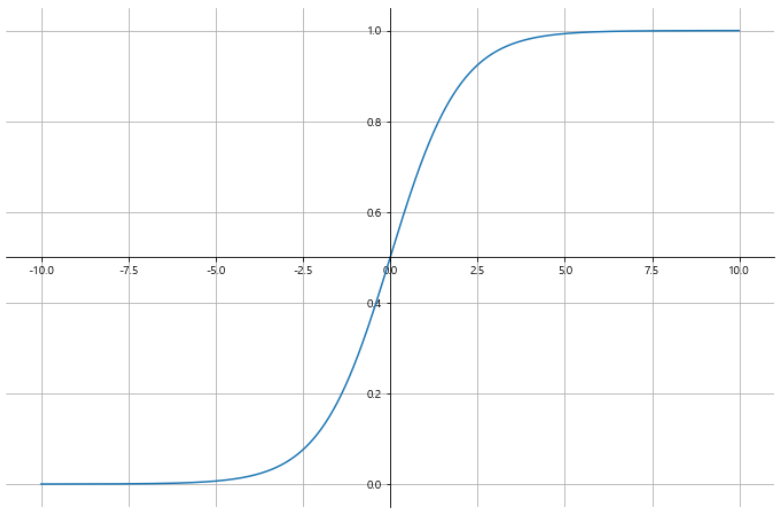
  • $h_{\theta}(x)$가 항상 0에서 1사이의 값을 갖도록 Hypothesis 함수 수정
    • $h_{\theta}(x)=g(\theta_{0}+\theta_{1}x)$ : 예측 결과가 1이 될 확률
    • $g(z)={1 \over {1+e^{-z}}}$

# 시그모이드(sigmoid)
plt.figure(figsize=(12, 8))
ax = plt.gca()

ax.plot(z, g)
ax.spines['left'].set_position('zero')
ax.spines['right'].set_color('none')
ax.spines['bottom'].set_position('center')
ax.spines['top'].set_color('none')
plt.grid()

plt.show()

• Decision Boundary : 기본 벡터공간을 각 클래스에 대하여 하나씩 두 개의 집합으로 나누는 초표면
  • $h_{\theta} = g(\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2})$
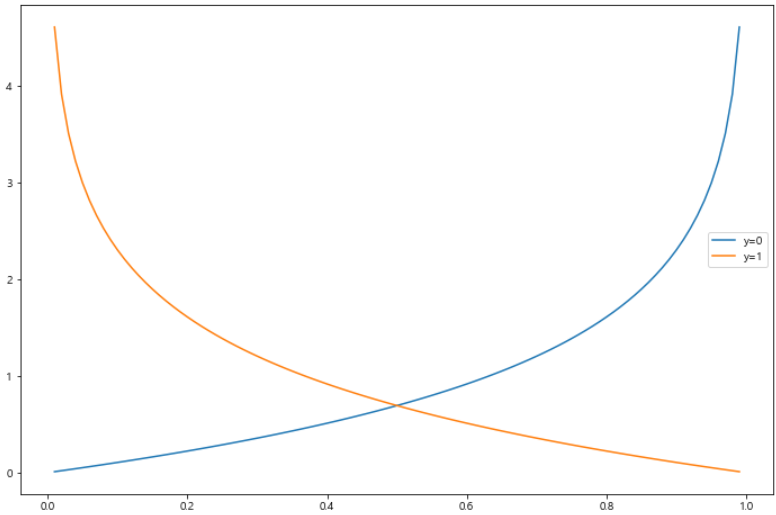
• Logistic Regression에서 Cost Function
  • ${1\over m}\sum_{i=1}^{m}{Cost(h_{\theta}(x^{(i)}), y^{(i)})}$
  • $Cost(h_{\theta}(x^{(i)}), y^{(i)}) = \left\{ \begin{matrix} -log(h_{\theta}(x)) & y = 1 \\ -log(1-h_{\theta}(x)) & y = 0 \end{matrix} \right.$
  • Learning 알고리즘은 동일
    • 수렴할 때까지 반복 : $\theta := \theta - \alpha{d \over d\theta}J(\theta)$

# Logistic Regression Cost Function
h = np.arange(0.01, 1, 0.01)

C0 = -np.log(1-h)
C1 = -np.log(h)

plt.figure(figsize=(12, 8))
plt.plot(h, C0, label='y=0')
plt.plot(h, C1, label='y=1')
plt.legend()
plt.show()

2. 실습

• 와인 데이터 사용

import pandas as pd

wine_red = pd.read_csv('../data/01/winequality-red.csv', sep=';')
wine_white = pd.read_csv('../data/01/winequality-white.csv', sep=';')

wine_red['color'] = 1
wine_white['color'] = 0
wine = pd.concat([wine_red, wine_white])
wine.reset_index(drop=True, inplace=True)
wine.head()

# taste 컬럼 추가
wine['taste'] = [1 if grade > 5 else 0 for grade in wine['quality']]

X = wine.drop(['taste', 'quality'], axis=1)
y = wine['taste']

# 데이터 분리
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=13)

• 기본 Logistic Regression
  • solver : 최적화 문제에 사용할 알고리즘
    1. iblinear : L1, L2 모두 지원, 작은 데이터에 적합한 알고리즘
    2. sag : L1만 지원, 확률적경사하강법을 기반으로 대용량 데이터에 적합한 알고리즘
    3. saga : L1, L2 모두 지원, 확률적경사하강법을 기반으로 대용량 데이터에 적합한 알고리즘
    4. newton-cg : L2만 지원, 멀티클래스의 분류 모델에 쓰이는 알고리즘
    5. lbfgs : L2만 지원, 멀티클래스의 분류 모델에 쓰이는 알고리즘
  • L1, L2에 대한 설명 : L1, L2

# Logistic regression
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

# solver : 최적화 알고리즘
# 데이터가 적은 경우 'liblinear' 주로 사용
lr = LogisticRegression(solver='liblinear', random_state=13)
lr.fit(X_train, y_train)

y_pred_tr = lr.predict(X_train)
y_pred_test = lr.predict(X_test)

print("Train Acc : {}".format(accuracy_score(y_train, y_pred_tr)))
print("Test Acc : {}".format(accuracy_score(y_test, y_pred_test)))

• Scaler와 Pipeline을 활용한 구축
  • 조금의 성능 상승 효과가 있음을 볼 수 있었다.

# Scaler와 pipeline을 활용한 구축
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

estimators = [('scaler', StandardScaler()),
              ('clf', LogisticRegression(solver='liblinear', random_state=13))]

pipe = Pipeline(estimators)

# fit(학습)
pipe.fit(X_train, y_train)

# 예측
y_pred_tr = pipe.predict(X_train)
y_pred_test = pipe.predict(X_test)

print("Train Acc : {}".format(accuracy_score(y_train, y_pred_tr)))
print("Test Acc : {}".format(accuracy_score(y_test, y_pred_test)))

• Decision Tree와 비교

# Decision Tree
from sklearn.tree import DecisionTreeClassifier

wine_tree = DecisionTreeClassifier(max_depth=2, random_state=13)
wine_tree.fit(X_train, y_train)

models = {'logistic regression' : pipe, 'decision tree' : wine_tree}

# roc_curve를 통한 비교
import matplotlib.pyplot as plt
import set_matplotlib_korean
from sklearn.metrics import roc_curve

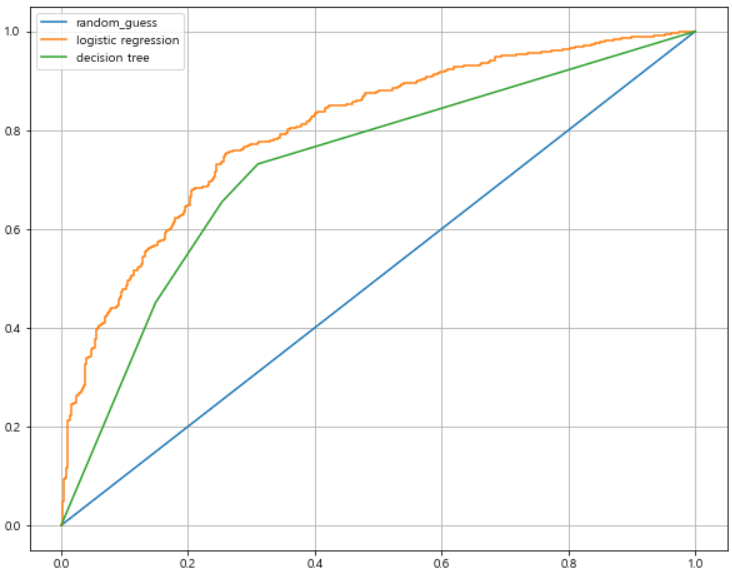
plt.figure(figsize=(10, 8))
plt.plot([0, 1], [0, 1], label='random_guess')
for model_name, model in models.items():
    pred = model.predict_proba(X_test)[:, 1]
    fpr, tpr, thresholds = roc_curve(y_test, pred)
    plt.plot(fpr, tpr, label=model_name)
plt.grid()
plt.legend()
plt.show()

◾PIMA 인디언 당뇨병 예측

• PIMA 인디언 : 멕시코와 미국에 걸쳐 살았던 인디언 부족
  • 50년대까지 PIMA 인디언은 당뇨가 없었다.
  • 20세기 말, 50%가 당뇨에 걸렸다.
  • 50년만에 50%의 인구가 당뇨에 걸렸다.
• 본래 강가에서 수렵하던 가난한 소수 인디언
• 미국 쪽 PIMA 인디언은 미국 정부에 의해 강제 이주 후 식량을 배급 받음
• 데이터 : Kaggle

# 데이터 읽기
import pandas as pd

PIMA = pd.read_csv('diabetes.csv')
PIMA.head()

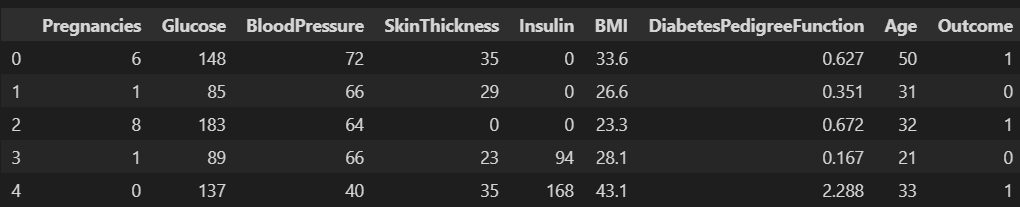
• 데이터 컬럼
  • pregnancies : 임신 횟수
  • Glucose : 포도당 부하 검사 수치
  • BloodPressure : 혈압
  • Skin Thickness : 팔 삼두근 뒤쪽의 피하지방 측정값
  • Insulin : 혈청 인슐린
  • BMI : 체질량지수
  • Diabetes Pedigree Function : 당뇨 내력 가중치 값
  • Age : 나이
  • Outcome : 클래스 결정, 당뇨 유무

# float형으로 변경
PIMA = PIMA.astype('float')
PIMA.info()

# 상관관계 확인
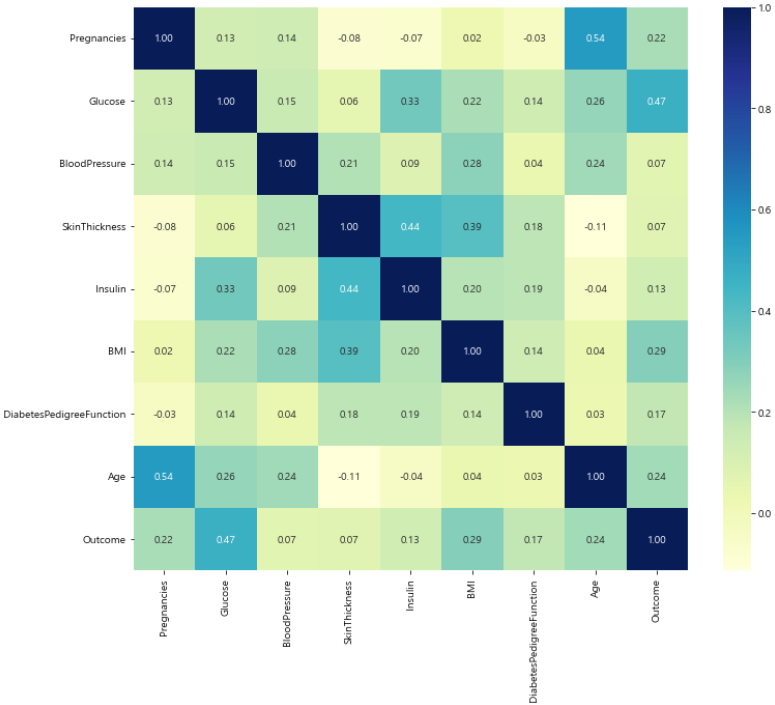
import seaborn as sns
import matplotlib.pyplot as plt
import set_matplotlib_korean

plt.figure(figsize=(12, 10))
sns.heatmap(PIMA.corr(), cmap='YlGnBu', annot=True, fmt='.2f')
plt.show()

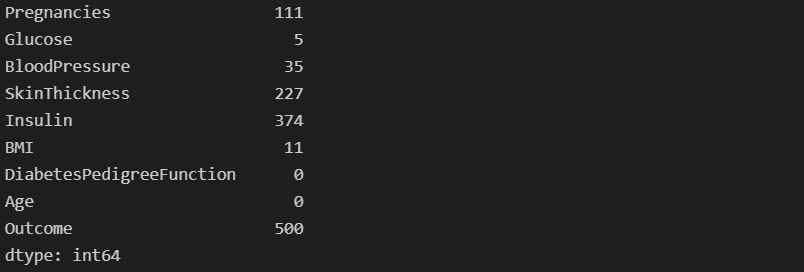
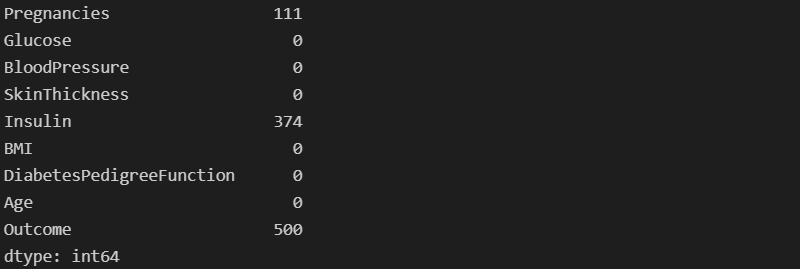
• BloodPressure(혈압)에 0이라는 숫자가 35개 있다.
• 확인이 필요하다.

# 데이터 확인
(PIMA == 0).astype(int).sum()

• 의학적 지식과 PIMA 인디언 정보가 없으므로 평균값으로 대체한다.

# 데이터 변경
zero_features = ['Glucose', 'BloodPressure', 'SkinThickness', 'BMI']
PIMA[zero_features] = PIMA[zero_features].replace(0, PIMA[zero_features].mean())
(PIMA==0).astype(int).sum()

# 데이터 나누기
from sklearn.model_selection import train_test_split

X = PIMA.drop(['Outcome'], axis=1)
y = PIMA['Outcome']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=13, stratify=y)

# Pipeline 구축
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression

estimators = [('scaler', StandardScaler()), 
              ('clf', LogisticRegression(solver='liblinear', random_state=13))]

pipe_lr = Pipeline(estimators)
pipe_lr.fit(X_train, y_train)
pred = pipe_lr.predict(X_test)

# 수치 확인
from sklearn.metrics import accuracy_score, recall_score, precision_score, roc_auc_score, f1_score

print("Accuracy : {}".format(accuracy_score(y_test, pred)))
print("Recall : {}".format(recall_score(y_test, pred)))
print("Precision : {}".format(precision_score(y_test, pred)))
print("AUC score : {}".format(roc_auc_score(y_test, pred)))
print("f1 score : {}".format(f1_score(y_test, pred)))

# 다변수 방정식의 각 계수값 확인
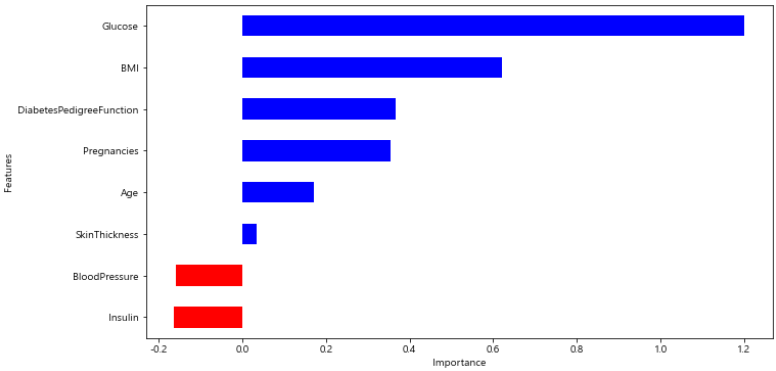
coeff = list(pipe_lr['clf'].coef_[0])
labels = list(X_train.columns)

# 주요 feature 그리기
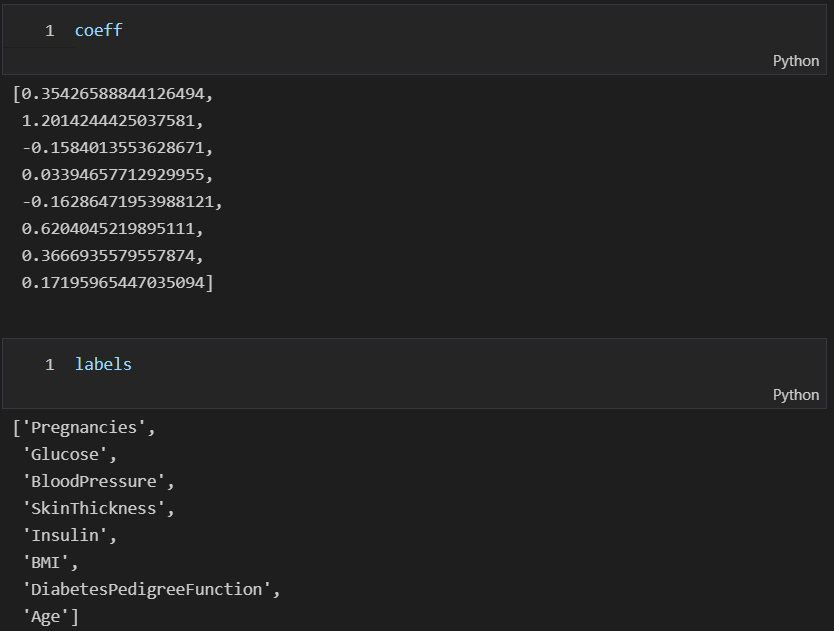
features = pd.DataFrame({'Features' : labels, 'importance' : coeff})
features.sort_values(by=['importance'], ascending=True, inplace=True)
features['positive'] = features['importance'] > 0
features.set_index('Features', inplace=True)
features['importance'].plot(kind='barh',
                            figsize=(11, 6),
                            color=features['positive'].map({True:'blue', False:'red'}))
plt.xlabel('Importance')
plt.show()