Neural Network Optimizer(Momentum, AdaGrad, RMSprop, Adam)

Optimizer

• 신경망 학습의 목적은 손실 함수의 값을 가능한 한 낮추는 매개변수를 찾는 것이다. 이는 곧 매개 변수의 최적값을 찾는 문제이며, 이러한 문제를 투는 것을 최적화(optimization)이라 한다.
• Optimizer는 optimization을 하기위해 보다 최적으로 gradient descent를 적용하고 손실함수의 최소 값으로 보다 빠르고 안정적으로 수렴할 수 있는 기법이다.

Momentum with SGD

• 가중치를 계속 Update 수행 시마다 이전의 Gradient들의 값을 일정 수준 반영 시키면서 신규 가중치로 Update적용
• SGD의 경우는 random한 데이터를 기반으로 Gradient를 계산하므로 최소점을 찾기 위한 최단 스텝형태로 가중치가 Update되지 못하고 지그재그 형태의 Update가 발생하기 쉽지만 Momentum을 통해서 이러한 지그재그 형태의 Update를 일정 수준 개선 가능하다.
• 모멘텀은 빠른 학습속도와 local minima의 문제를 해결하고자 SGD에 물리의 관성의 개념을 적용한것이다.
  
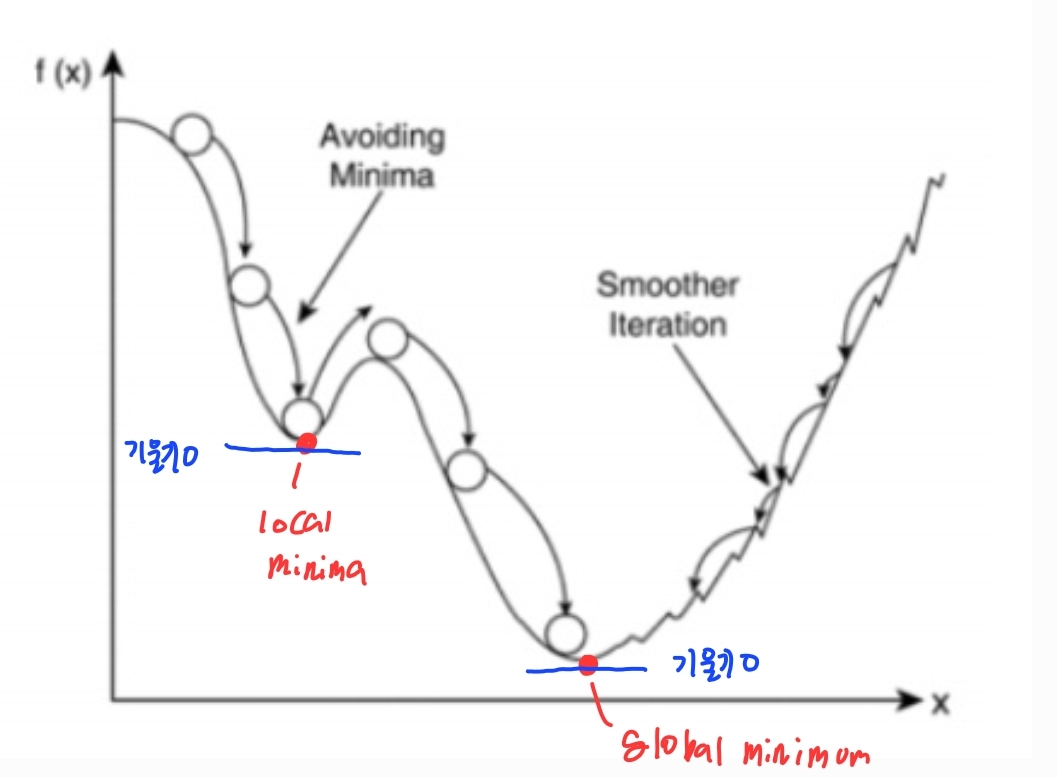
• 일반 SGD:
  
  
  
  $W_{t+1} = W_{t} - \alpha\frac{\nabla{Loss}}{\nabla{W_{t}}}$
  
  $\alpha=학습률\quad t=iteration$
  
  
  
• Momentum SGD:
  
  
  
  $W_{t+1} = W_{t} - V_{t}$
  
  $V_{t} = V_{t-1} + \alpha\frac{\nabla{Loss}}{\nabla{W_{t}}}$
  
  $\alpha=학습률\quad t=iteration$
  
  
  
• 일반적으로 관성계수인 r은 보통 0.9로 한다.

keras.optimizers.SGD(Ir, momentum, decay, nesterov)

• Ir: 0보다 크거나 같은 float 값. 학습률
• momentum: 0보다 크거나 같은 float값. SGD를 적절한 방향으로 가속화하며, 흔들림(지동)을 줄여주는 매개변수
• decay: 0보다 크거나 같은 float값. 업데이트마다 적용되는 학습룰의 감소율
• nesterov: 불리언값. 네스테로프 모멘텀의 적용여부

AdaGrad(Adaptive Gradient)

• 가중치를 업데이트 하는 과정에서 학습률 값이 중요하다. 이 값이 너무 작으면 학습시간이 너무 길어지고, 반대로 너무 크면 발산하여 학습이 제대로 이루어지지 않는다. 학습률을 정하는 효과적인 기술로 학습률 감소가 있는데 이는 학습을 진행하면서 학습률을 점차 줄여나가는 방법이다. 처음에는 크게 학습하다가 조금씩 작게 학습하는 것이다. AdaGrad는 이를 더욱 발전시킨 방법이다.
• 가중치 별로 서로 다른 Learning Rate를 동적으로 적용
• iteration 시마다 개별 가중치별로 적용된 Gradient의 제곱값을 더해서 Learning Rate를 새롭게 적용
• 처음에는 큰 Learning rate가 적용되지만 최저점에 가까울 수록 Learning rate가 작아진다.
• 수식:
  
  
  
  $W_{t+1} = W_{t} - \frac{\alpha}{\sqrt{S_{t} + \epsilon}} \frac{\nabla{Loss}}{\nabla{W_{t}}}$
  
  $S_t = S_{t-1} + (\frac{\nabla{Loss}}{\nabla{W_{t}}})^2$
  
  $\alpha=학습률\quad t=iteration$
  
  
  

  여기서 엡실론은 아주작은 수로 루트안이 0이 되는걸 방지한다.

• AdaGrad는 과거의 기울기를 제곱하여 계속 더해간다. 그래서 학습을 진행할수록 갱신 강도가 약해진다. 실제로 무한히 계속 학습을 한다면 어느 순간 갱신량이 0이 되어 전혀 갱신되지 않게 된다. 이 문제를 개선한 기법이 RMSProp이다.

RMSProp

• AdaGrad에서 Learning rate가 지나치게 감소하는걸 막고자 Gradient의 제곱값을 더하는 것이 아닌 지수 가중 평균볍을 사용한다.
  
  
  
  $W_{t+1} = W_{t} - \frac{\alpha}{\sqrt{S_{t} + \epsilon}} \frac{\nabla{Loss}}{\nabla{W_{t}}}$
  
  $S_t = \gamma S_{t-1} + (1-\gamma) (\frac{\nabla{Loss}}{\nabla{W_{t}}})^2$
  
  $\alpha=학습률\quad t=iteration$
  
  
  
• 감마값으로는 보통 0.9를 사용한다.

keras.optimizers.RMSprop(Ir, rho, epsilon, decay)

• Ir: 0보다 크거나 같은 float 값. 학습률\
• rho: 0보다 크거나 같은 float 값. 감마값으로 default값=0.9
• epsilon: 0보다 크거나 같은 float. None인 경우 K.epsilon()이 사용된다.
• decay: 0보다 크거나 같은 float 값. 업데이트마다 적용되는 학습률의 감소율

Adam(Adaptive Moment Estimation)

• RMSProp 과 Momentum의 결합
  
  
  
  $RMSProp$
  
  
  
  $W_{t+1} = W_{t} - \frac{\alpha}{\sqrt{S_{t} + \epsilon}} \frac{\nabla{Loss}}{\nabla{W_{t}}}$
  
  $S_t = \gamma S_{t-1} + (1-\gamma) (\frac{\nabla{Loss}}{\nabla{W_{t}}})^2$
  
  

---

$momentum$



$W_{t+1} = W_{t} - V_{t}$

$V_{t} = V_{t-1} + \alpha\frac{\nabla{Loss}}{\nabla{W_{t}}}$

---

$Adam$



$W_{t+1} = W_{t} - \frac{\alpha}{\sqrt{S_{t} + \epsilon}}V_{t}$

$V_{t} = \beta_1V_{t-1} + \beta_1*\frac{\nabla{Loss}}{\nabla{W_{t}}}$

$S_t = \beta_2 S_{t-1} + (1-\beta_2) (\frac{\nabla{Loss}}{\nabla{W_{t}}})^2$

keras.optimizers.Adam()

• Ir: 0보다 크거나 같은 float 값. 학습률
• beta_1: 0보다 크고 1보다 작은 float값. 일반적으로 1에 가깝게 설정된다.
• beta_2: 0보다 크고 1보다 작은 float값. 일반적으로 1에 가깝게 설정된다.
• epsilon: 0보다 크거나 같은 float. None인 경우 K.epsilon()이 사용된다.
• decay: 0보다 크거나 같은 float 값. 업데이트마다 적용되는 학습률의 감소율
• amsgrad: Adam의 변형인 AMSGrad값 불리언