PCA (Principle Component Analysis), 주성분 분석

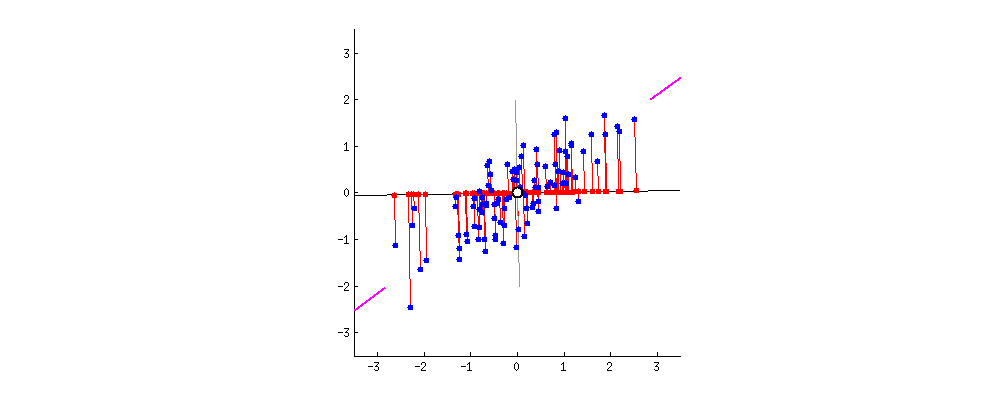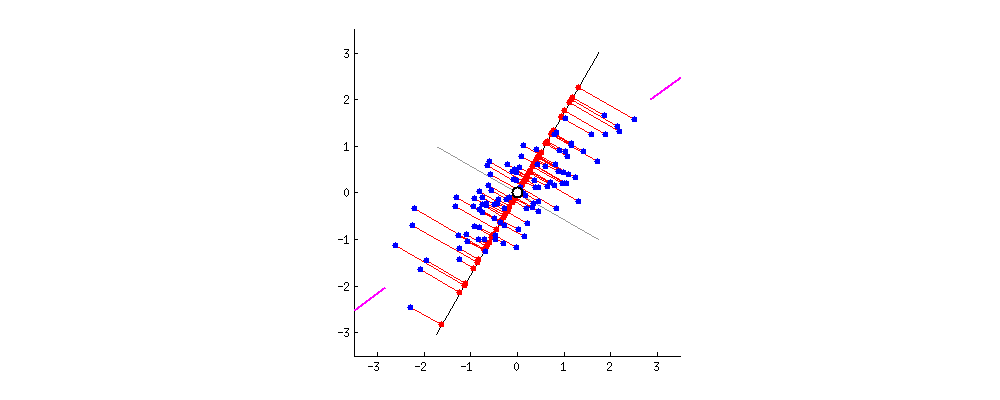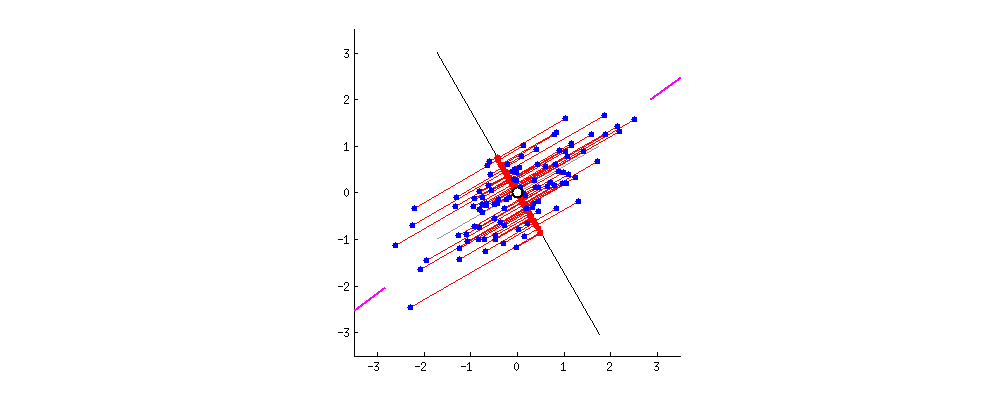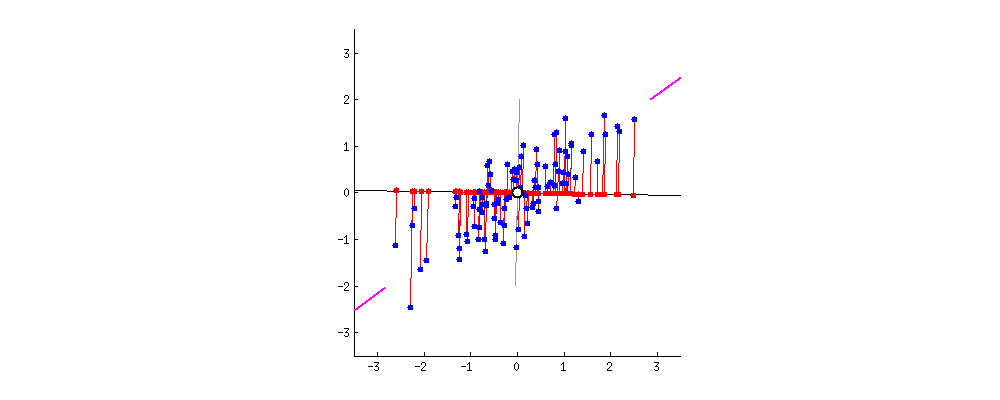
분산을 최대한으로?

PCA란 차원축소기법중 하나로 말 그대로 "주"성분을 분석하는 것이다.

2차원의 데이터가 있을때 이를 하나의 1차원 으로 축소한다고 하였을때 이를 축소할수 있는 방법은 다음과 같다.
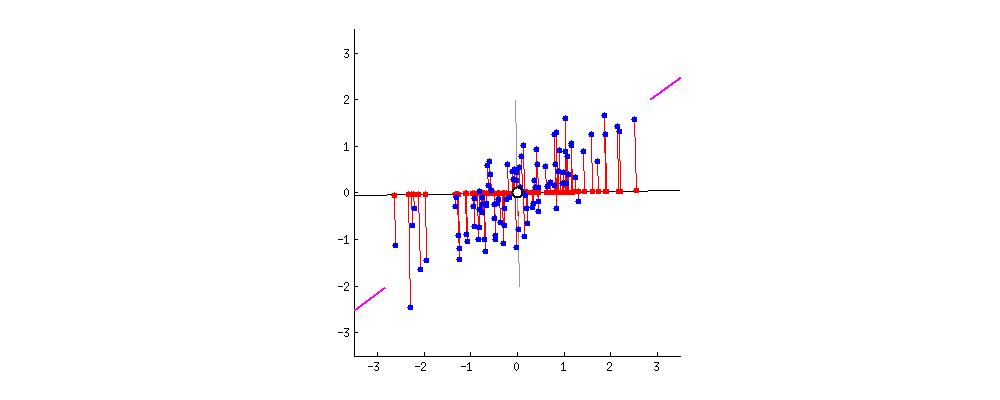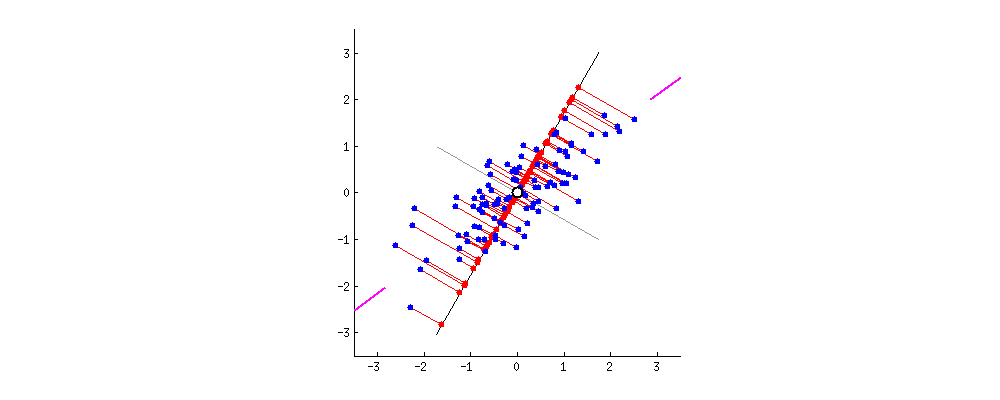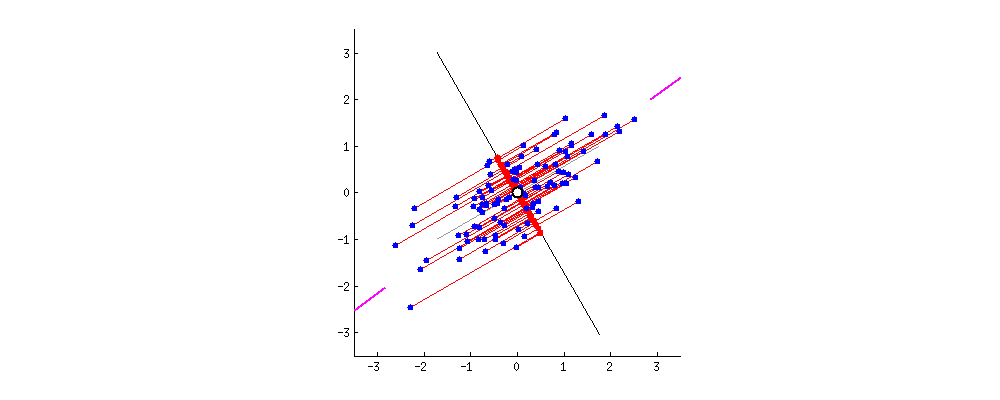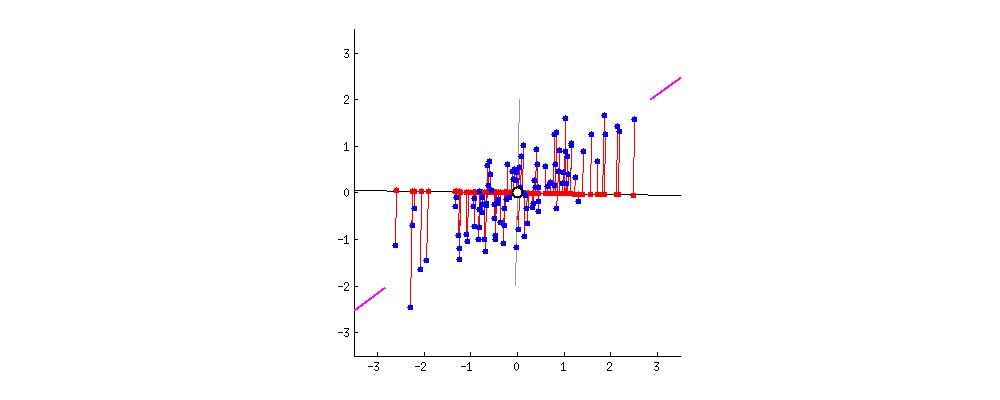출처:https://butter-shower.tistory.com/210

이때 PCA는 분산을 최대로 보존할 수 있는 축을 선택하는 것이 정보를 가장 적게 손실할 수 있을것이라는 생각으로 만들어진 기법이다.

3차원데이터를 2차원 데이터로 축소할 경우는 다음과 같다.
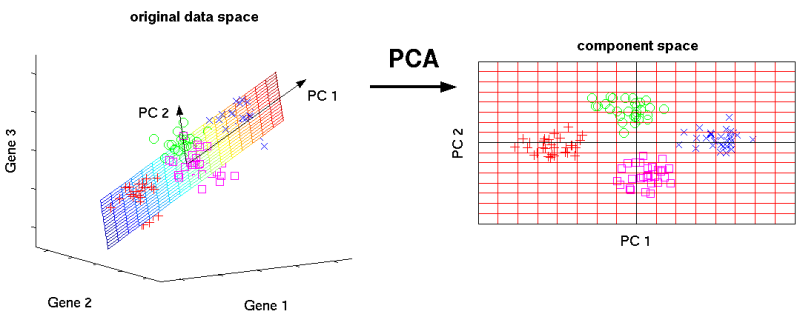출처:https://m.blog.naver.com/sanghan1990/

2차원 데이터로 축소를 한다는 말은 곧 투영을 해야하는 평면을 찾아야하는것이다.
평면은 2개의 독립인 벡터로 만들수 있으며 이 2개의 독립인 벡터(PC1, PC2)를 찾아야한다.
먼저 분산이 최대가 되는 방향으로 PC1을 찾고 그 축과 수직이면서 분산이 최대가 되는 PC2를 찾으면 된다.

PCA 기법의 요약.

분산을 최대한 보존하는 방향으로 주성분 추출
변동성을 최대로 하는 축을 찾는다.(PC1)
PC1에 수직이고, 변동성이 큰 축을 잡아간다.(PC2, PC3...)
주성분으로 만든 공간으로 사영시킨다.

주성분을 찾는법

PCA의 처음부터 끝까지 과정을 살펴보면 다음과 같다.
출처:https://dinhanhthi.com/img/post/ML/dim_redu/pca

1. 위의 table을 보게 되면 x1~x5 까지 총 5개의 feature를 가지고 있다. 즉, 5차원의 data set이다. 먼저 이 data set으로 분산 공분산 행렬(Covariance matrix)를 만든다.

• 분산 공분산 행렬(Covariance matrix):

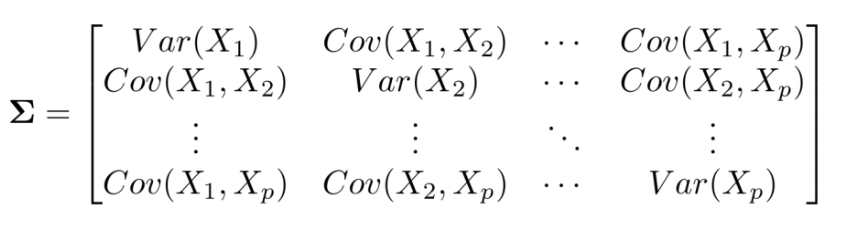
2. 그 다음 Covariance matrix 에 대한 eigen value(고유값) 와 eigen vertor(고유 벡터)를 구한다.

   • eigen value(고유값) 와 eigen vertor(고유 벡터):
     $Ax = \lambda x$
     $\lambda$ = $고유치$, $x$ = $고유치에 해당하는 고유 벡터$

3. 고유값이 큰 순서대로 정렬하고 이에 따른 고유벡터가 순서대로 PC1, PC2..가 된다.

4. 원본 데이터를 구해준 주성분 (PC1, PC2..)방향으로 회전하여 데이터를 정사영 시킨다.

PCA 기법 사용시 필요한 개념

• Explained Ratio = n번째 고유값 / 고유값의총합
  공분산행렬의 계산을 통해서 차원을 줄이면 원본 데이터의 분산을 몇% 보존하는가?
  n개의 해당하는 Explained Ratio를 더해주면 차원을 줄였을때 분산을 몇%보존했는지 계산할 수 있게 된다.

• 데이터의 표준화
  PCA기법이란 분산을 최대화하는 방향을 찾는것인데 주어진 데이터 자체로 공분산 행렬을 만들게 되면 절대값이 튼 데이터의 영향으로 편향이 생길수 있다. 그래서 scaling을 통해 변수변환을 해준다.

  표준화(Standard Scaler)
  $z = \frac{value - mean}{standard deviation}$