
💡차원축소
PCA 설명에 앞서 차원축소의 개념을 먼저 설명하고 가도록하겠다.
아래의 데이터 프레임을 보게되면 총 13개의 열로 13차원의 벡터로 표현된다. 이와 같은 고차원의 데이터는 계산과 시각화가 어려워 분석하기가 쉽지 않다.

따라서 원 데이터의 분포를 가능한 유지하면서 데이터의 차원을 줄이는것을
차원축소(dimensionality reduction)이라고 한다.
🔑Introduction to PCA
주성분 분석(PCA)는 가장 널리 사용되는 차원 축소 기법 중 하나로, 원 데이터(original data)의 분포를 최대한 보존하면서 고차원 공간의 데이터들을 저차원 공간으로 변환한다.
PCA는 기존의 변수들의 선형결합을 통하여 서로 연관성이 없는 새로운 변수, 즉 주성분(PC)들을 만들어낸다. 이때, 만들수 있는 PC의 최대 개수는 원데이터의 변수의 개수만큼 만들 수 있다.
PCA는 원 데이터의 분포를 최대한 보존하기 위해 분산을 최대로 하는 축을 찾아 주 성분으로 사용해야한다.
2차원 data의 pca를 진행된다면 최대 2개의 주축을 만들 수 있다. 아래 그림은 첫번째 주축인 PC1()을 찾는것을 기하학적으로 보여준다.
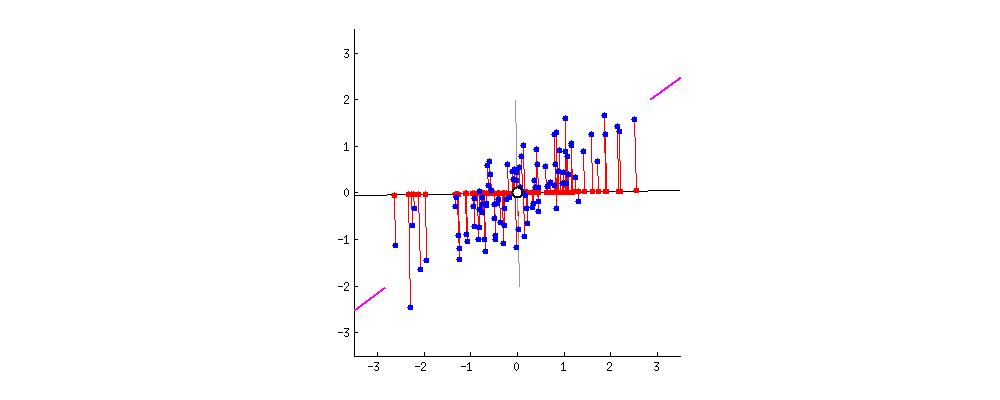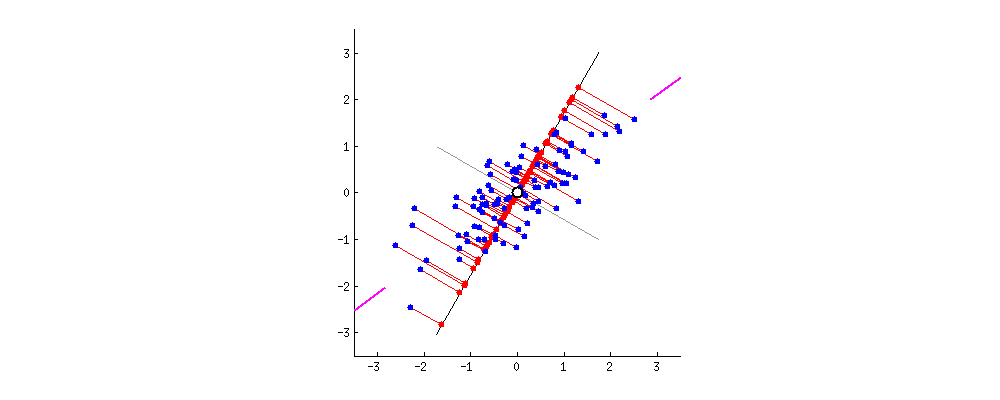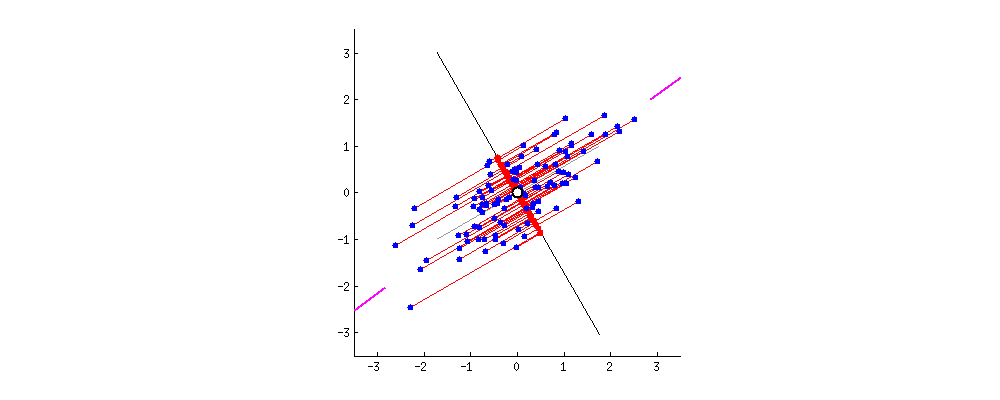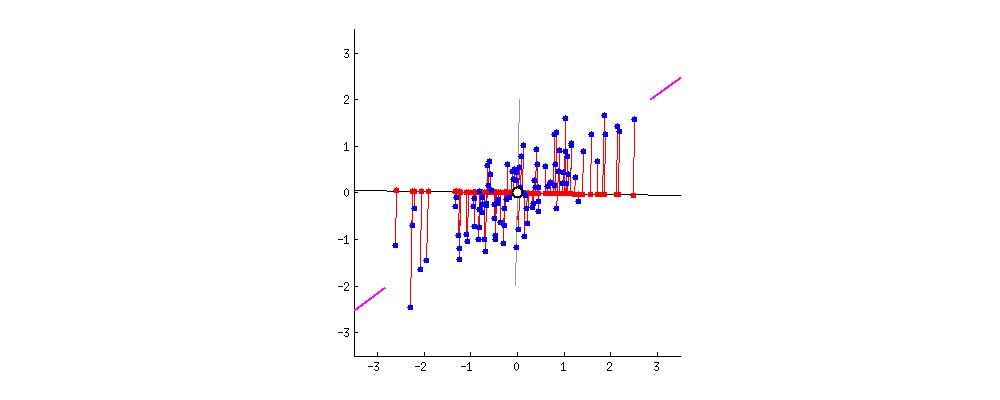
축이 돌아 가면서 2차원 데이터가 PC1()에 정사영이 되고 이들의 축이 돌아감에 따라 이들의 분산을 구해보면 다음과 같다.

PCA는 분산을 최대로 하는 축을 찾아주는 것이라고 했다. 따라서 빨간색으로 칠해진 것이 첫번째 주축이 될 것이다.
이때 두번째 주축인 PC2는 PC1의 수직인 축이고 이때 PC2의 분산은 다음과 같이 구할수 있다.
주성분(pc)들이 수직이여야하는 이유 = 주성분들 사이에는 서로 관계가 없도록 해야한다. 이는 서로 다른 주축이 수직을 이루는 것으로 나타낸다.
요약:
- PCA란 주어진 데이터의 변수들의 선형결합으로 "새로운 변수"인 주성분 (PC)를 찾는것이다.
- 찾을수 있는 주성분의 최대 개수 = 데이터의 변수들의 개수
- 주성분들 사이는 서로 관계가 없다.(uncorrelated)
- Mean-centered or Standardized data를 사용해야 한다.
- n차원의 데이터가 있을때 분산의 합은 PC1~PC의 분산의 합과 같다.
🔑Mathmatics of PCA
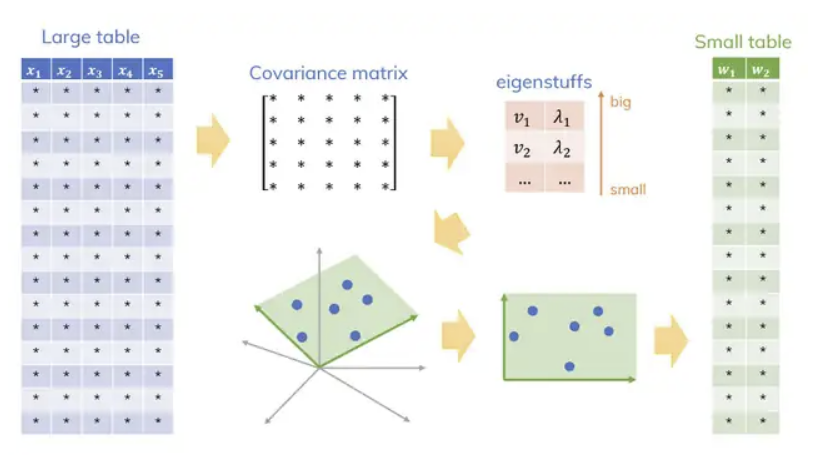
PCA는 간단히 말하면 주어진 데이터의 분산공분산행렬(covariance matrix)의 고유치와 고유벡터를 구하는 과정이고 이는 아래 2가지 방법으로 구할 수 있다.
- Singular value decomposition(SVD) of data matrix
- Spectral decomposition of covariance matrix
먼저 를 mean-centered data matrix, 를 분산공분산행렬이라고하면 아래와 같은 식이 성립된다.(이때 n은 의 행의 개수이다.)
SVD, Spectral decomposition 둘중 하나를 이용해 아래와 같은 방법으로 분산공분산 행렬의 고유치와 고유벡터를 구할 수 있다.

이를 요약해 PCA과정을 설명하겠다.
📌PCA의 과정
👉 데이터 프레임 가 주어졌다고 하자 이를 mean-centerd data matrix로 바꾸어준다.
👉최종적인 목표는 의 분산 공분산 행렬인 의 eigenvalue() 와 eigenvector를 구하는 것이다.
👉위에 설명한 2가지 방법중 한가지를 선택한다.
1.Spectral decomposition of covariance matrix 사용시:
목표 eigenvalue = 구한 eigenvalue
2. Singular value decomposition(SVD) of data matrix 사용시:
구한
목표 eigenvalue = 구한 eigenvalue(n = 데이터 행의 개수)
💡eigen vector와 eigenvalue의 의미
아래 3차원 mean-centered data matrix가 주어졌다고 하자.
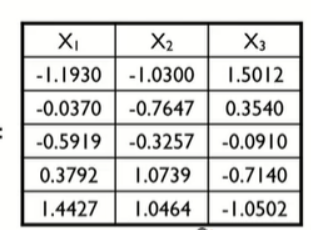
이때 eigenvalue 와 그에 해당하는 eigenvector는 다음과 같다.
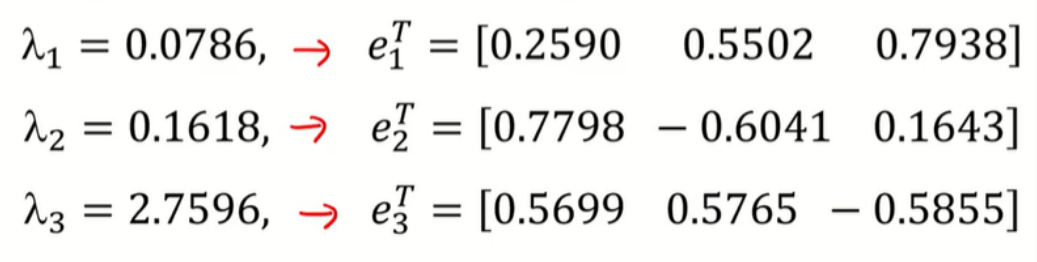
이때 은 분산이 제일 큰 PC인 PC1의 분산이다.
구하고자 하는 (PC1~PC3)를 (Z1~Z3)라 하면 고유벡터는 기존 데이터의 열벡터들()의 선형결합의 계수역할을 한다.

💡몇개의 PC를 써서 차원축소를 해야할까?
-
고유값 감소율이 유의미하게 낮아지는 Elbow Point에 해당하는 주성분 수를 선택
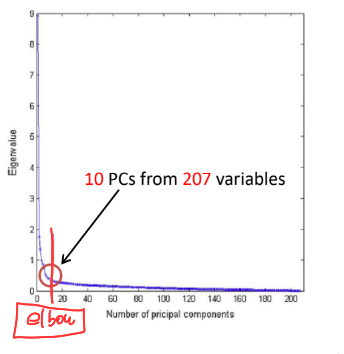
-
일정 수준 이상의 분산비를 보존하는 최소의 주성분을 선택(보통 70%이상)
참고:
https://dinhanhthi.com/img/post/ML/dim_redu/pca
https://butter-shower.tistory.com/210


