orthogonal matrix(직교행렬) 과 matrix of orthonormal columns

orthogonal matrix(직교행렬)의 정의

직교행렬은 정방행렬이면서($n$x$n$) 행벡터들이 모두 수직이고, 열벡터들이 모두수직인 동시에, 열과 행 벡터의 크기가 1인 행렬을 말한다.
즉, 행렬의 열이 orthonormal vecotr(정규 직교 벡터)로 이루어진 행렬이다.

직교행렬은 제일 중요한 성질은 각도,길이,내적을 보존하는 행렬이라는 것이다.

직교행렬($Q$) 의 성질:

• $Q^{-1} = Q^T$
• $Q^TQ = I$
• $||Qv|| = ||v||$
• $(Qx)^T(Qy) = x^Ty$
• 두 직교행렬의 곲은 직교행렬이다.

$Q^TQ = I$ 인 이유는 다음과 같다.

직교행렬($Q$)는 정규직교벡터들의 집합인($q_1, q_1, ...q_n$) 으로 이루어진 ($n$x$n$)행렬이다.

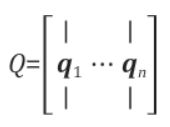
$Q^TQ$를 보게되면 대각원소는 열벡터 자기 자신끼리의 내적이므로 1이되고 나머지 원소는 정규직교 집합은 자신을 제외한 나머지의 벡터와는 수직이므로 내적이 0이된다.

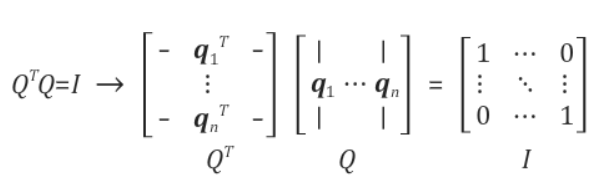
$||Qv|| = ||v||$인 이유는 다음과 같다.
벡터의 크기는 자기 자신과의 내적 또는 transpose와의 내적으로 표현할 수 있다.

$(Qv)^TQv = v^Tv$
$v^TQ^TQv = v^Tv$

$Q^TQ$는 $I$이므로 $||Qv|| = ||v||$인 것을 확인할수 있다.

matrix of orthonormal columns

직교행렬이란 ($n$ x $n$)인 정방행렬만 가능했다 만약에 행렬의 열이 정규직교벡터들로 이루어져 있지만 정방행렬이 아닌 ($m$ x $n$) 행렬로 이루어져있으면 어떤 성질을 가지게 될까 알아보겠다.

($m$ x $n$) 행렬$U$ 의 열이 정규 직교 벡터들도 이루어져있으면 다음과 같은 성질을 가지게 된다.

$U^TU = I_{n}$
$||Ux|| = ||x||$
$(Ux)\cdot(Uy) = x\cdot y$
$(Ux)\cdot(Uy) = 0 \leftrightharpoons x\cdot y = 0$