공분산은 두 변수 간에 양의 상관관계가 있는지, 음의 상관관계가 있는지를 알려준다.
=
이제 그래프를 통하여 공분산은 무엇인지 또 왜저러한 수식으로 표현되는지 알아보도록 하겠다.
= [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
= [3, 5, 7, 9, 12, 11, 13, 18, 20, 29]
다음과 같은 값을 표로 그려 보면 다음과 같다.
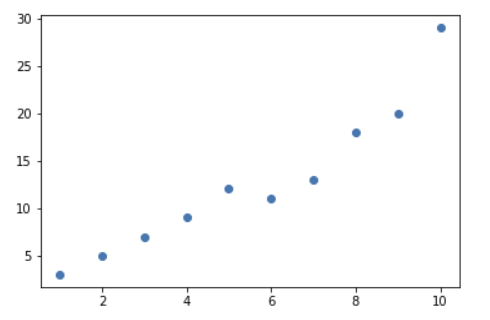
이때 의 평균을 구해서 해당 평균으로 영역을 나누면 다음과 같다.
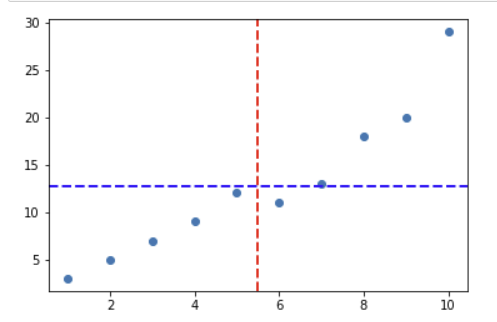
그래프를 보게되면 x와 y의 평균을 기준으로 4개의 구역이 생기게 된다.
를 기준으로 오른쪽은 값이 양수가 되고 왼쪽은 음수가된다.
를 기준으로 위쪽은 값이 양수가 되고 아래쪽은 음수가된다.
따라서 을 통해 양수가 되는 구역과 음수가 되는 구역으로 나뉠수 있게 된다.
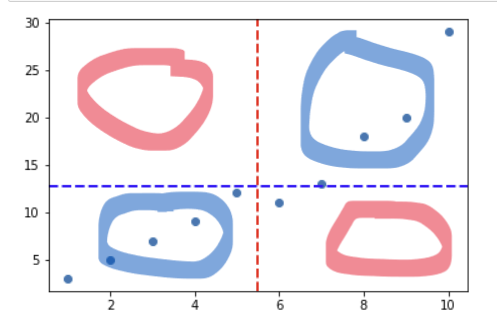
파란색이 칠해져있는 영역은 가 양수가 되는 영역이고 빨간색이 칠해져있는 영역은 가 음수가 되는 영역이다.
다시 공분산의 식을 살펴보겠다.
=
즉 공분산은 를 모두 더한후 평군을 낸 값으로 공분산이 양수라면 두 변수는 양의 상관관계를 가지는것이고 음수라면 양의 상관관계를 가지는 것이다.
하지만 공분산은 특이값에 영향을 많이 받고 두 변수가 관계를 가지는 방향성만 말해주지 강도의 크기는 말해주지 않는다.
상관계수(Coefficient of Correlation)
상관계수는 공분산의 단점을 커버한 것이라고 생각하면된다. 공분산은 값이 양수냐 음수냐 이 2가지 부분으로만 해석할 수 있지만 👍상관계수는 값의 크기로도 해석할 수 있다.
식을 보게되면 상관계수는 두 변수 간의 공분산 을 각각 의 표준편차와 의 표준편차로 나눈 식이다.
상관 계수로 두 변수간의 해석은 다음과 같이 할 수 있다.
상관계수가 0이다. -> 두 변수는 선형 관계를 가지고 있지 않다.
상관계수가 양수이다. -> 두 변수는 선형적으로 양의 상관관계를 가지고 있다.
상관계수가 음수이다. -> 두 변수는 선형적으로 음의 상관관계를 가지고 있다.
그렇다면 상관계수가 양수일때 0.5 과 0.9는 어떤 차이가 있을까?

상관계수가 1일때는 perfect positive correlation 으로 완전한 양의 선형 관계를 가지고 있다는 것이고 상관계수가 0.5일때는 low positive correlation 으로 양의 선형 관계를가지긴 하지만 직선으로 부터 어느정도 퍼져있는것을 확인할 수 있다.
즉, 상관계수의 크기는 두 변수사이에 얼마나 강한 상관관계를 가지고 있는냐를 알수있다.
> 0.8 강한 상관관계
0.5<< 0.8 중간정도의 상관관계
<0.5 약한 상관관계
