정규분포란 무엇일까?
정규분포(normal distribution)은 연속 확률 분포의 하나로 종 모양을 띄고 있다.
자연현상, 사회현상 등은 정규분포형태의 확률분포를 많이 따르게 된다.
정규분포 ~ (,):
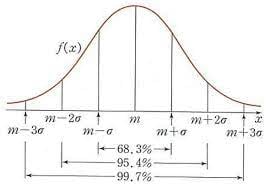
정규분포의 특징은 다음과 같다.
평균을 중심으로 좌우 대칭이다.
면적이 확률이된다
평균으로 부터 표준편차가 몇칸인지에 따라 확률이 결정된다.
평균으로 부터 표준편차가 몇칸인지에 따라 확률이 결정된다.이 말이 뭘 뜻하는지 그림으로 알아보겠다.
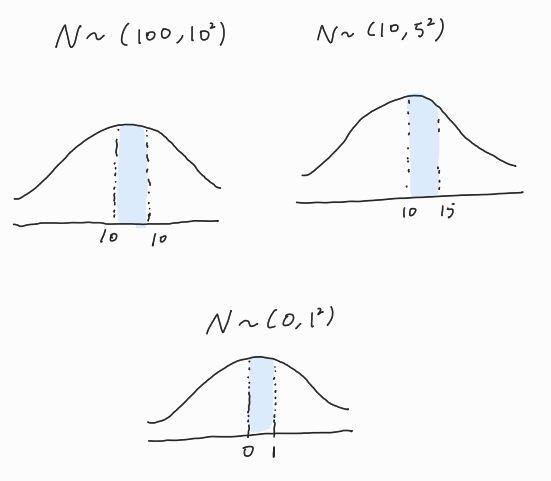
파란색으로 칠해져있는 구간의 면적이 같다는 것이다.
정규분포의 모양
정규분포의 모양은 평균과 분산에의해 결정되는데 분산이 클수록 넓게 퍼져있다는 뜻이므로 완만한 종모양이되고 분산이 잘을수록 평균에 가깝게 몰려있다는 뜻이므로 뾰족한 종모양이 생성된다.
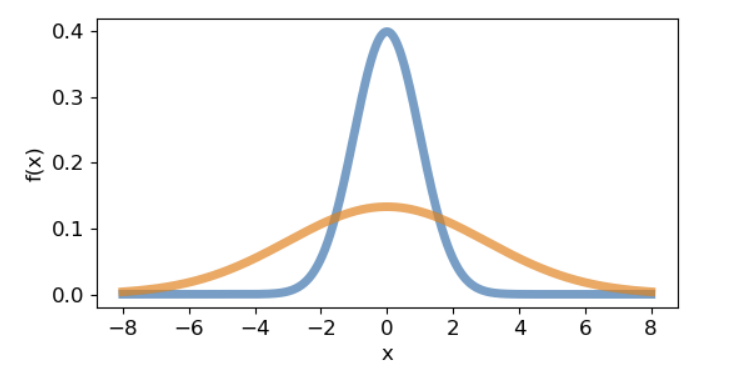
파란색은 ~ (,), 주황색은 ~ (,)
표준 정규 분포
표준 정규 분포란 평균이 0, 표준편차가 1인 정규분포이다.
표준 정규 분포: ~ (,)
표준 정규 분포표
표준 정규 분포의 면적을 계산해놓은 표이다.
정규분포의 표준화
정규분포의 표준화 공식은 다음과 같다.
그렇다면 이 공식이 어떻게 나왔는지 알아보도록 하겠다.
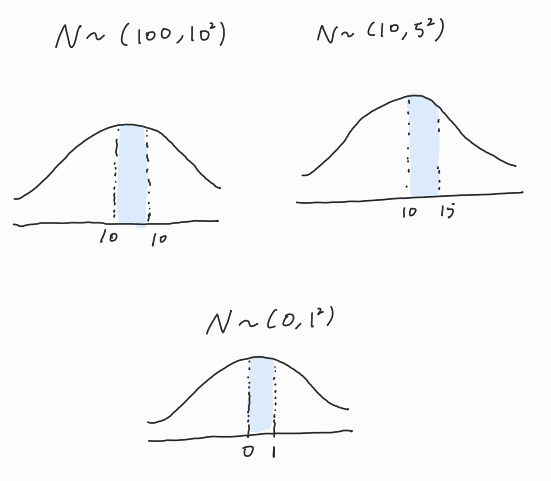
위의 3면적의 크기는 전부 동일하게 평균으로 부터 한칸의 표준편차가 떨어져있으므로 파란색으로 칭해진 면적의 크기는 동일하다.
따라서, 표준 정규 분포의 면적을 계산해놓은 표준 정규 분포표 를 이용해 정규분포의 면적의 확률을 구할수 있게 되는것이다.
위에서 말했지만 면적의 크기는 평균으로 부터 몇칸의 표준편차가 떨어져있는냐로 결정이 난다고 했다.
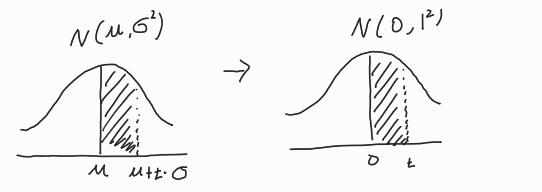
에서 를 빼면 0이되고
에서 를 빼준후 로 나누어 주게 되면 t가 된다.
이때문에 를 사용해 정규분포를 표준정규 분포로 바꿔 확률을 계산하는것이다.
