링크

한줄요약

문제의 조건을 강제로 적용하는 것도 하나의 방법!

문제

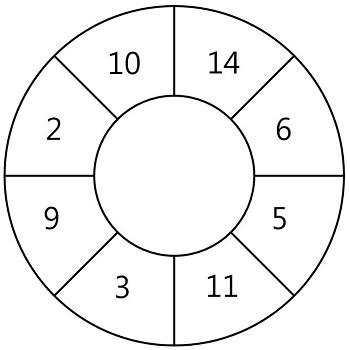
사진과 같은 스티커 판이 있다.
1) 원형으로 연결된 스티커 판에서 몇 장의 스티커를 뜯어내어 뜯어낸 스티커에 적힌 숫자의 합이 최대가 되도록 만든다.

2) 한 칸의 스티커를 때면 인접한 양옆의 스티커를 땔 수 없다. (예: 14를 때면, 10과 6은 땔 수 없다.)

3) 사진과 같은 스티커의 정보는 1차원 배열로 주어진다. 예시) [14, 6, 5, 11, 3, 9, 2, 10]

정리

다이나믹 프로그래밍을 사용해서 문제를 정리해보면 다음과 같다.

1. d[i]
   d[i]는 i번재 스티커를 때거나 안땟을때 얻을 수 있는 최대값

2. 점화식
   d[i] = max(d[i-1], d[i-2] + a[i])
   i번째 스티커를 안때면 i-1 번째 스티커를 땐다.
   i번째 스티커를 때면 i-2번째 스티커를 때고 i번재 스티커를 땐다.
   위와 같이 점화식을 세울 수 있다.

3. 원형...
   하지만 문제가 있다. 원형인데 마지막 스티커를 때려면 제일 처음 스티커를 때면 안된다.
   그냥 아싸리 1) 첫번째 스티커를 땠을 때, 2) 첫번째 스티커를 때지 않았을 때로 나눠서 각각 계산하고, 두 결과를 비교해서 최대값을 구해준다.

코드

#include <vector>
#include <algorithm>

#define max_int 100001
using namespace std;

//시간 복잡도: O(n)
//공간 복잡도: O(n)
//사용한 알고리즘: 동적 계획법, Bottom-Up
//사용한 자료구조: 1차원 배열


// d[i]는 i번재 스티커를 때거나 안땟을때 얻을 수 있는 최대값
int d[max_int];

int solution(vector<int> sticker)
{
    int answer, size;
    size = (int)sticker.size();

    // 0. 예외처리 1) 길이가 1 - 첫번째 스티커 반환, 2) 길이가 - 두개 중 큰거 반환
    if(size == 1) return sticker[0];
    else if(size == 2) return max(sticker[0], sticker[1]);
    else{

        // 1. 첫번째 스티커를 땠을 때
        d[0] = sticker[0];
        d[1] = sticker[0];

        for(int i=2; i<size - 1; i++){
            d[i] = max(d[i-2] + sticker[i], d[i-1]);
        }
        answer = d[size - 2];

        // d 배열 초기화
        for(int i=0; i<size; i++) d[i] = 0;

        // 2. 첫번째 스티커를 안땠을 때
        d[0] = 0;
        d[1] = sticker[1];

        for(int i=2; i<size; i++){
            d[i] = max(d[i-2] + sticker[i], d[i-1]);
        }

        answer = max(answer, d[size - 1]);

        return answer;
    }
}