1. stack 이란 무엇인가요?
1) 정의
스택은 나중에 들어온 것이 제일 먼저 나오는 자료구조입니다.
2) 용어
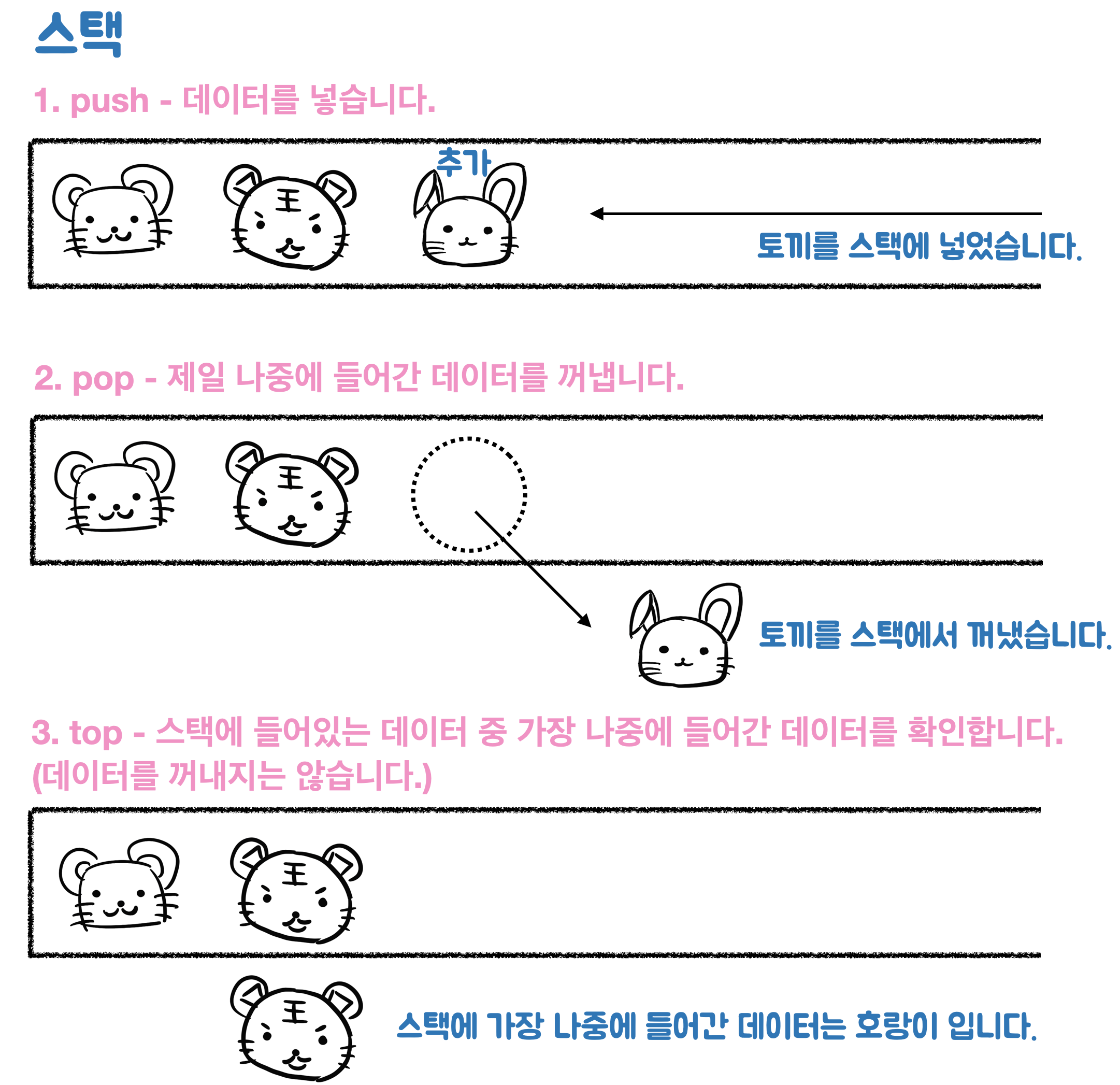
스택에 대해 3가지 용어가 있습니다.
- push - 삽입 - 데이터를 넣음
- pop - 삭제 - 나중에 들어간 데이터를 지움
- top - 확인 - 나중에 들어간 데이터를 확인
3) 스택과 비슷한 모습
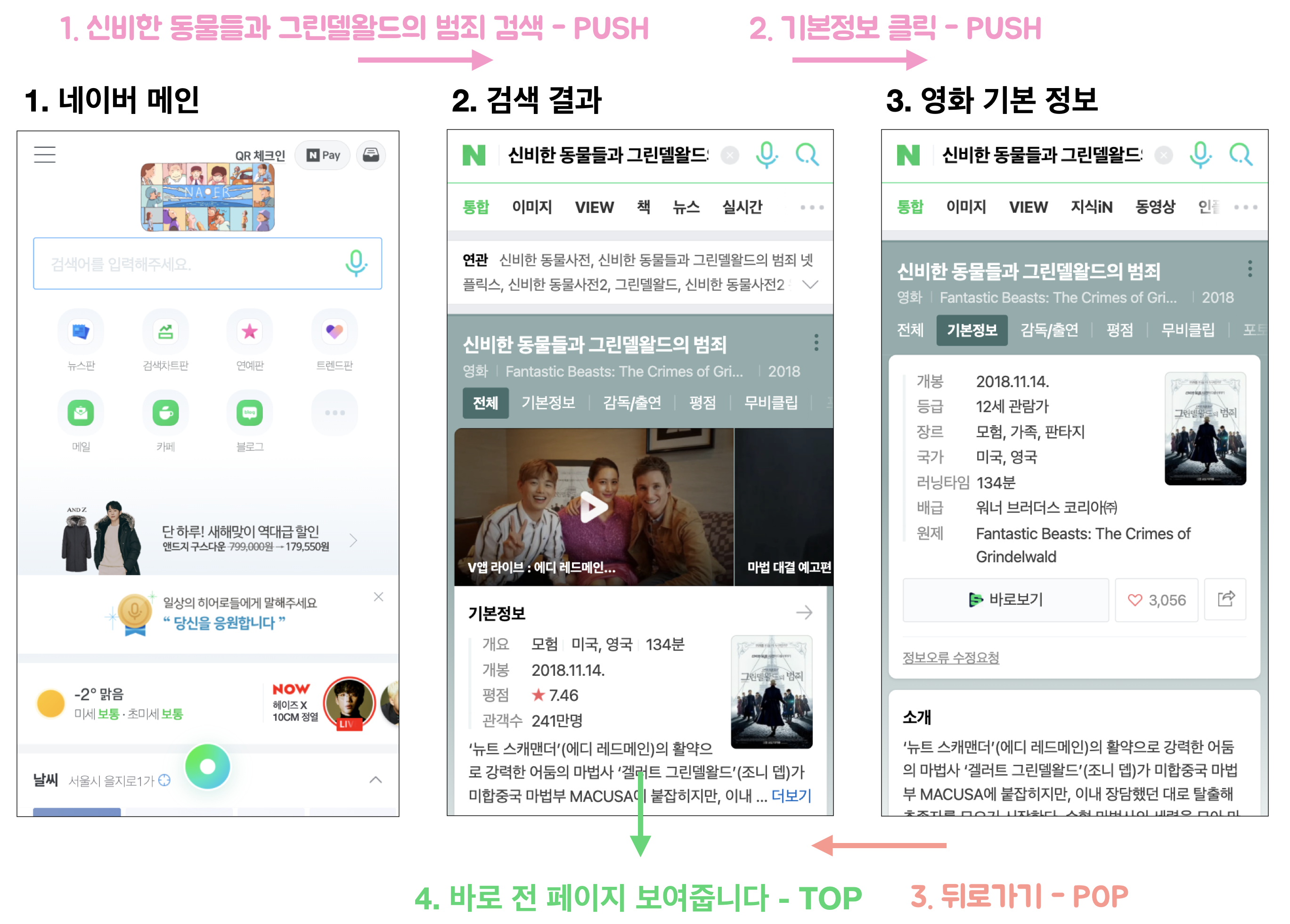
스택과 비슷한 모습을 한 것으로는 프링글스 통, 쌓아놓은 책들이 있는데요, 제일 많이 사용하는 곳 중 하나는 브라우저의 뒤로가기 버튼입니다.
네이버에서 영화를 검색한 결과인데요,
3번째 영화 기본 정보에서 뒤로가기를 누르면 2번째 검색 결과로 이동합니다.
3가지 스택의 연산에 비유하면,
-
새로운 페이지로 이동하면 - PUSH
-
뒤로가기 버튼을 누르면, 현재 보고 있는 페이지 - POP
-
바로 전 페이지 보여주기 - TOP
4) 후입선출 (LIFO)
나중에 들어온것이 제일 먼저 나온다는 말을 사자성어로 후입선출 이라고 하며, 영어로는 Last In First Out 줄여서 LIFO 라고 합니다.
음, 평소에 자주 사용하는 단어가 아니라서, 어렵게 느껴질 수 있어요. 사실 크게 신경쓰지 않아도 될거 같아요!
2. 그런데, 왜 stack 자료구조를 사용하나요?
무엇인가를 거꾸로 탐색하는데 효율적으로 사용할 수 있기 때문입니다.
이 처럼 거꾸로 진행하기 위해서는 3가지 연산이 효율적으로 수행되어야하는데,
1) 제일 나중에 들어간 것을 꺼내는 연산 - pop
2) 제일 나중에 들어간 것을 확인하는 연산 - top
3) 새로운 데이터를 넣는 연산 - push
스택은 3가지 연산 pop, top, push 를 각각 수행하는데 O(1)로 아주 빠릅니다.
시간 복잡도가 O(1) 이라는 의미는 연산 단 1번을 의미합니다.
O(1)은 정말 짧은 시간으로 상수 시간이라고도 부릅니다.
3. 언어별 사용법
1) c++
c++에는 stack이라는 스택을 위한 라이브러리가 있습니다.
다만, vector를 사용하는 경우도 많습니다.
왜냐하면 stack 라이브러리를 사용하는 경우 인덱스를 사용한 접근이 안되지만, vector를 사용하는 경우 index를 사용해서 접근할 수 있기 때문입니다.
- stack을 사용한 경우
#include <iostream>
// 1. 스택 라이브러리를 사용합니다.
#include <stack>
using namespace std;
// 2. 스택을 생성합니다.
stack<int> s;
int main() {
// 3. push - 스택에 데이터를 넣습니다.
s.push(1);
s.push(2);
s.push(3);
// 4. pop - 스택에 가중 나중에 들어간 데이터를 꺼냅니다.
s.pop();
// 5. 스택에 있는 데이터 중 가장 나중에 들어간 데이터를 확인합니다.
cout << s.top() << endl;
// 6. 반복문을 사용해서, 나중에 들어간 데이터부터 스택에서 전부 꺼냅니다.
while(!s.empty()) {
cout << s.top() << endl;
s.pop();
}
}- vector를 사용한 경우
#include <iostream>
// 1. vector 라이브러리를 사용합니다.
#include <vector>
using namespace std;
// 2. 벡터 템플릿을 사용해서 스택을 생성합니다.
vector<int> s;
int main() {
// 3. push - 스택에 데이터를 넣습니다.
s.push_back(1);
s.push_back(2);
s.push_back(3);
// 4. pop - 스택에 가중 나중에 들어간 데이터를 꺼냅니다.
s.pop_back();
// 5. 스택에 있는 데이터 중 가장 나중에 들어간 데이터를 확인합니다.
cout << s[s.size() - 1] << endl;
// 6. 인덱스 접근을 사용해서 먼저 들어간 데이터 부터 확인합니다.
for(int i=0; i<s.size(); i++) {
cout << s[i] << endl;
}
// 7. 반복문을 사용해서, 나중에 들어간 데이터부터 스택에서 전부 꺼냅니다.
while(s.size() > 0) {
cout << s[s.size() - 1] << endl;
s.pop_back();
}
}2) java
// 1. 스택 라이브러리를 사용합니다.
import java.util.Stack;
public class Main {
public static void main(String args[]) {
// 2. 스택을 생성합니다.
Stack<Integer> s = new Stack<>();
// 3. push - 스택에 데이터를 넣습니다.
s.push(1);
s.push(2);
s.push(3);
// 4. pop - 스택에서 데이터를 꺼냅니다.
s.pop();
// 5. peek - 스택에 가장 나중에 들어간 데이터를 확인합니다.
// java에서는 top이라고 하지 않고, peek입니다.
System.out.println(s.peek());
// 6. 반복문을 사용해서, 나중에 들어간 데이터부터 스택에서 전부 꺼냅니다.
while(!s.empty()) {
System.out.println(s.peek());
s.pop();
}
}
}3) python
파이썬의 경우 stack 라이브러리를 따로 import 하지 않고, 기본 list 를 stack으로 충분히 사용할 수 있습니다.
# 1. 파이썬 기본 리스트를 사용해서 스택을 생성합니다.
s = []
# 2. push - 스택에 데이터를 넣습니다.
s.append(1)
s.append(2)
s.append(3)
# 3. pop - 스택에서 데이터를 꺼냅니다.
s.pop()
# 4. 스택에 있는 데이터 중 가장 나중에 들어간 데이터를 확인합니다.
print(s[len(s) - 1])
# 5. 반복문을 사용해서, 나중에 들어간 데이터부터 스택에서 전부 꺼냅니다.
while len(s) > 0:
print(s[len(s) - 1])
s.pop()4) javascript
// 1. 기본 리스트를 사용해서 스택을 생성합니다.
s = []
// 2. push - 스택에 데이터를 넣습니다.
s.push(1)
s.push(2)
s.push(3)
// 3. pop - 스택에서 데이터를 꺼냅니다.
s.pop()
// 4. top- 스택에 가장 나중에 들어간 데이터를 확인합니다.
console.log(s[s.length - 1])
// 5. 반복문을 사용해서 스택에 나중에 들어간 데이터 부터 전부 꺼냅니다.
while(s.length > 0) {
console.log(s[s.length - 1])
s.pop()
}5. 재귀함수와 stack overflow
1) 재귀함수
갑자기 왜 재귀함수가 나오냐구요?
사실, 재귀함수는 내부적으로 스택을 사용합니다.
조금 더 정확하게 말해서, 스택 메모리라고 부릅니다.
만약, 다음 재귀함수를 실행하면, 아래처럼 호출됩니다.
public class Main {
// 1. 재귀를 사용해서, 1 부터 처음 받은 수까지 1씩 증가하면서 출력하는 함수
public static void print_num(int num) {
// 2. 중요!!!, 0 일때 재귀를 종료합니다.
if(num == 0) return;
// 3. num을 1감소해서 재귀함수 호출
print_num(num - 1);
// 4. 3번에서 반환되면 여기로 오게되고 인자값으로 받은 num을 출력합니다.
System.out.println(num);
}
public static void main(String args[]) {
print_num(3);
}
}
/*
결과
1
2
3
*/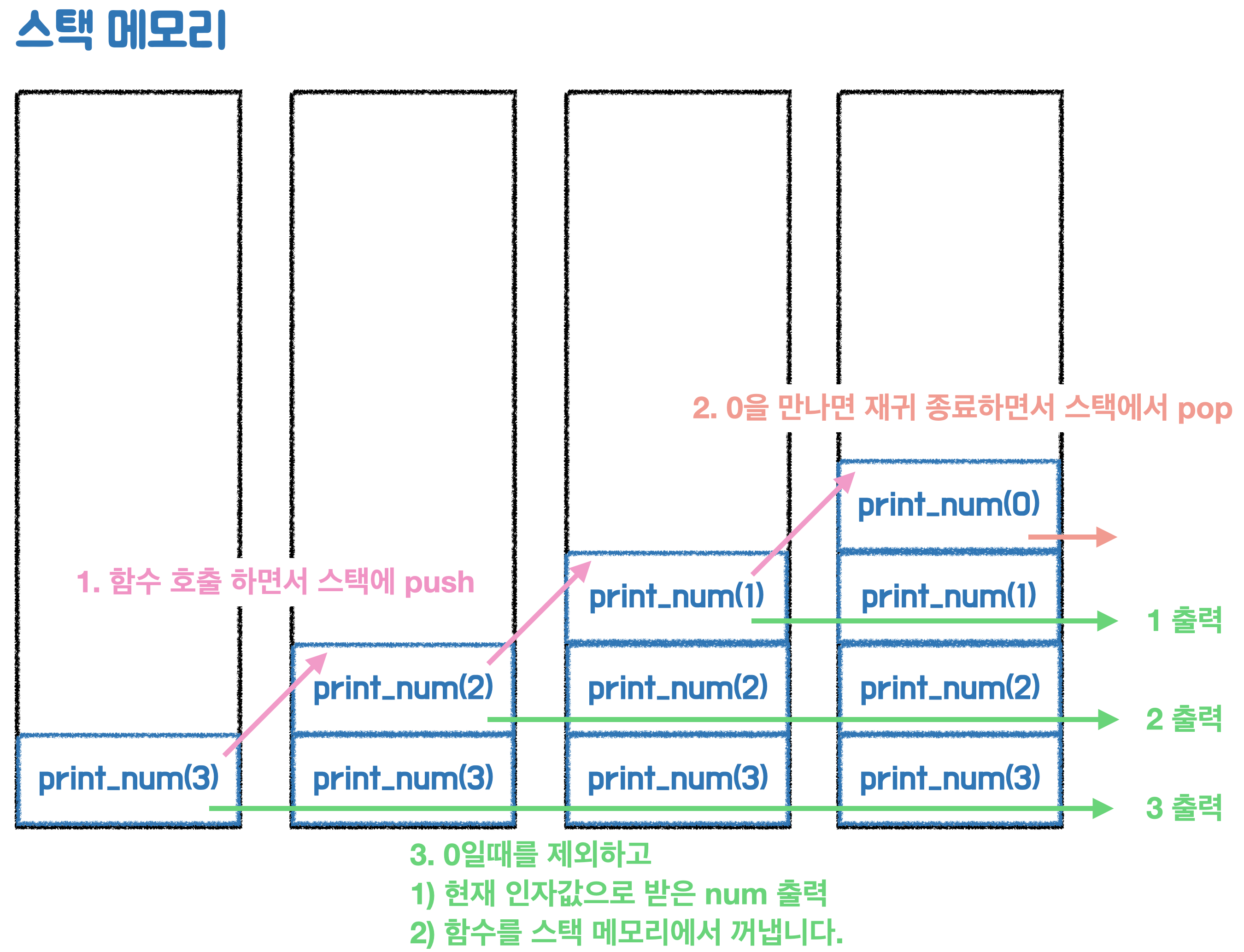
2) stack overflow
만약 위의 재귀함수를 0일때 종료시키지 않으면 어떻게 될까요?
스택 메모리에 지속적으로 함수가 쌓이게 됩니다.
컴퓨터는 프로그램을 실행할때 스택 메모리의 크기를 고정하고 실행되는데 이 부분이 넘쳐흐릅니다.
이를 stack overflow 스택 오버 플로우 라고 합니다.
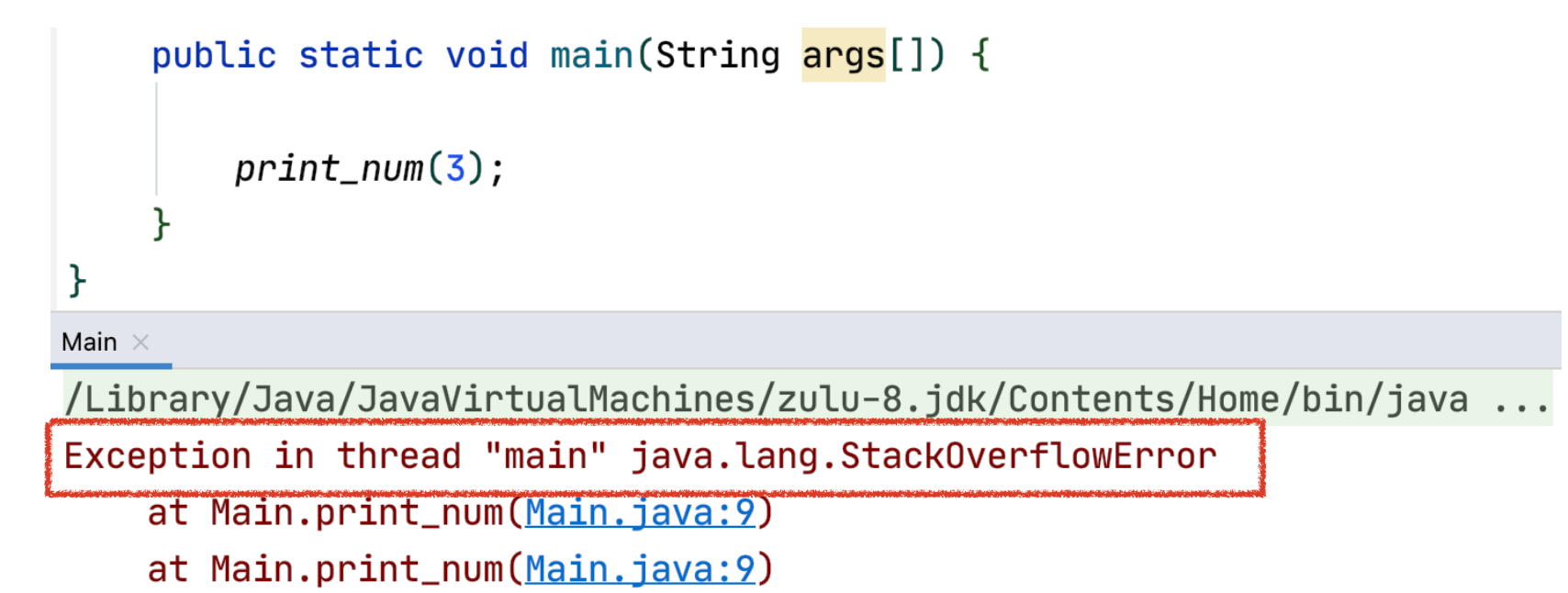
위의 코드에서 0일때 종료하는 부분을 주석처리하고 실행하면, stack overflow가 발생합니다.
public class Main {
// 1. 재귀를 사용해서, 1 부터 처음 받은 수까지 1씩 증가하면서 출력하는 함수
public static void print_num(int num) {
// 2. 0 일때 재귀를 종료합니다.
//if(num == 0) return;
// 3. num을 1감소해서 재귀함수 호출
print_num(num - 1);
// 4. 3번에서 반환되면 여기로 오게되고 인자값으로 받은 num을 출력합니다.
System.out.println(num);
}
public static void main(String args[]) {
print_num(3);
}
}
6. stack은 어느 곳에서 사용되나요?
다양한 알고리즘에서 사용되지만, 대표적으로 2곳이 있습니다.
- 1) 무엇인가를 거꾸로 꺼낼때
- 2) DFS (너비 우선 탐색)
재귀함수(recursive)는 내부적으로 스택을 사용합니다. 이러한 이유로 DFS(깊이 우선 탐색)이 스택으로 구현이 가능하지만, 재귀로도 구현이 가능합니다. 그리고, 더 간편해서 재귀를 많이 사용합니다.
DFS (너비 우선 탐색)에 대한 자세한 내용은 다음에 알아보도록 해요.
7. stack을 이해하는데 도움이 되는 문제
사실, 스택 하나만을 사용해서 푸는 알고리즘 문제는 많지 않습니다. 크게 유형은 2가지 입니다.
- 스택과 다른 알고리즘을 함께 사용하는 문제
- 스택으로 풀것 같지 않은 문제
1) 백준 10828 - 스택
문제 링크
스택을 직접 구현하는 문제입니다. 한 번 해보면, 스택이 어떻게 동작하는지 바로 이해할 수 있습니다.
2) 백준 9012 - 괄호
문제 링크
처음 보면, 스택을 어떻게 사용해야 하지? 라고 생각이 들 수 있어요.
제일 나중에 들어간 것이 무엇인지 확인할때는 스택을 사용하면 빨리 찾을 수 있습니다.
3) 백준 15685 - 드래곤 커브
조금 어려울 수 있는데요, 패턴을 찾고 스택을 사용하면 편리해집니다.
제가 작성한 드래곤 커브 문제 풀이 입니다.
