혹시, 다음에 해당하시나요?

1. 공부하다가 재귀가 나오면 퍽 하고 숨이 막히고, 어지럽다.
2. 재귀를 사용하면 불안해서 반복문을 사용한다.
3. 내가 짠 재귀는 무한히 호출될것 같다.
4. 어떤 값을 반환해야할지 모르겠다.

역시 for문이 짱이지

지금부터, 다음 3가지에 초점을 맞추고, 재귀를 쉽게 알아볼께요

1. 함수의 의미 정의
2. 어떤 값을 반환해야 하나요?
3. 언제 종료해야 하나요?

1. 100부터 1까지 더한 결과 계산

조금 쉬운 예시로 알아볼께요.

100부터 1까지 모두 더한 결과를 계산하는 함수(sum_result)를 반복문으로 만들면 다음과 같습니다.

#include <stdio.h>

int sum_result(int num) {
    int result = 0;
    
    for(int i=num; i>=1; i--){
        result = result + i;
    }
    
    return result;
}

int main(){
    printf("%d\n", sum_result(100));
}

이제 이 함수(sum_result)를 재귀로 바꿔볼거에요!

1) 함수의 의미 정의

int sum_result(int num)

sum_result(num) 함수는 num 까지 계산한 결과를 반환합니다. 라고 정의합니다.
그러면, sum_result(num) 은 num ~ 1 까지 더한 결과 반환
sum_result(num-1) 은 num-1 ~ 1 까지 더한 결과 반환
sum_result(1) 은 1 반환

sudo 코드로 return 부분을 작성하면 다음과 같아요

int sum_result(int num) {
	return num 까지 모두 더한 결과
}

2) 어떤 값을 반환해야 하나요?

어떤 값을 return 해야할까요?
함수가 호출될때 마다 1) 특정 정수가 2) 지금까지 계산한 결과에 더해져요.

그래서 이말을 조금 바꾸면, 다음과 같아요.

함수가 호출될때 마다 인자값으로 받은 정수 num이 num-1 ~ 1 까지 계산한 결과에 더해져요.

int sum_result(int num) {
	return num + sum_result(num-1);
}

3) 언제 종료해야 하나요?

1까지 모두 더했다면, 0은 더해지면 안되요. 따라서, num이 0일때 함수가 호출되면 더하지 않고 종료시켜 주어야합니다.

sudo 코드로 작성해보면

int sum_result(int num) {
      
    if(num == 0) {
      return 함수종료
    }
  
    return num + sum_result(num-1);
}

음... 함수의 반환값은 int이기 때문에 정수를 반환해야해요. 0일 때도 무엇을 반환해야하기는 하는데. 덧셈 결과에 영향을 안주려면!! 0을 반환합시다.

#include <stdio.h>

int sum_result(int num) {
      
    if(num == 0) {
      return 0;
    }
  
    return num + sum_result(num-1);
}

int main(){
    printf("%d\n", sum_result(100));
}

만약에 0을 반환하는게 싫다, 덧셈이니까 0 반환해도 괜찮지 곱셉일때는 어떻게 하냐? 생각할 수 있어요.

그러면 조금 바뀌서, 0 바로 전 1에서 1을 반환하면서 종료시키면되요.

#include <stdio.h>

int sum_result(int num) {
      
    if(num == 1) {
      return 1;
    }
  
    return num + sum_result(num-1);
}

int main(){
    printf("%d\n", sum_result(100));
}

2. 피보나치 수

피보나치 수는 다음과 같습니다.

1, 1, 2, 3, 5, 8, 13, 21...

• 1번째 피보나치 수:1
• 2번째 피보나치 수: 1
• 3번째 피보나치수: 2

따라서, n번째 피보나치 수를 d[n]이라고 할때 다음 점화식을 만족합니다. (n은 3이상)

// n이 3이상일 때 다음을 만족합니다.
d[n] = d[n-1] + d[n-2]

문제
입력으로 숫자 n이 주어졌을때 n번째 피보나치 수를 구하세요.

재귀로 풀어봅시다.

fibo(i)함수는 반드시 i 번째 피보나치수를 돌려준다고 생각해봐요

int fibo(int i)

그러면 fibo(i-1)은 반드시 i-1번째 피보나치수를 돌려주고
fibo(i-2)는 반드시 i-2번째 피보나치수를 돌려줘요

그 2개를 더한 결과가 반드시, i번째 피보나치수 이에요.

#include <stdio.h>
#define max_int 10001

int n, d[max_int];

int fibo(int i){
    /*
    중요2. (언제 끝나야할지를 몰라서)
    
    i가 2보다 작거나 같을때 점화식을 만족하지 않기 때문에
    재귀함수를 더 이상 호출하지 않습니다.
    */  
    if(i <= 2){
        return 1;
    }
    /*
    중요2. (언제 끝나야할지를 몰라서)
    
    이미 한번 계산했을때 (d[i] 가 0이 아닐때) 
    계산한 값을 반환합니다.
    */      
    if(d[i] > 0) return d[i];
    
    /*
     중요1. (어떤 값이 반환될지를 몰라서)
     
     fibo(i)함수는 반드시 i 번째 피보나치 수를 돌려준다고 생각해봐요
     그러면 fibo(i-1)은 반드시 i-1번째 피보나치 수를 돌려주고
     fibo(i-2)는 반드시 i-2번째 피보나치 수를 돌려줘요
     그 2개를 더한 결과가 반드시, i번째 피보나치 수 이에요.
     */
    return d[i] = fibo(i-1) + fibo(i-2);
}

int main(){
    // n 입력
    scanf("%d", &n);
    
    // fibo(n)은 반드시 n번째 피보나치 수를 돌려줘요.
    printf("%d\n", fibo(n));
}

뭔 X소리냐고, 할 수 있는데 잠시만 기다려봐요, 잠시만

이분탐색까지만 보고가요, 제발

3. 이분탐색 (binary search)

이렇게 해봅시다.

/*
start - 시작 인덱스
end - 마지막 인덱스
array - 정렬된 수가 들어있는 배열
num - 찾아야할 값
*/
int binary_search(int start, int end, int *array, int num)

믿읍시다.
위 함수는 반드시, 정렬된 배열(array)에서 정수(num)가 몇번째 인덱스에 있는지를 찾아준다고.

그러면 재귀가 조금더 짜기 쉬워져요

#include <stdio.h>

/*
 다음 함수는 오름차순으로 정렬된 배열 array에 대해
 시작 인덱스: start, 마지막 인덱스: end 일때
 정수 num의 인덱스를 반드시 찾아줍니다.
 */
int binary_search(int start, int end, int *array, int num){
    int mid = (start + end) / 2;

    if(start <= end){
        if(array[mid] < num){
            /*
            중요1. (어떤 값이 반환될지를 몰라서)
            
            다음 호출 binary_search(mid + 1, end, array, num)은 
            mid + 1 ~ end 구간에서 정수 num의 인덱스 번호를 반드시 찾아줍니다.
            그래서 바로 return 합니다.
            */
            return binary_search(mid + 1, end, array, num);
        }
        else if(array[mid] == num){
	        /*
    		중요2. (언제 끝나야할지를 몰라서)
            
    	    정수 num을 찾았을때 종료합니다.
	        */
            return mid;
        }
        else{
            /*
            중요1. (어떤 값이 반환될지를 몰라서)
            
            다음 호출 binary_search(start, mid - 1, array, num)은 
            start ~ mid - 1 구간에서 정수 num의 인덱스 번호를 반드시 찾아줍니다.
            그래서 바로 return 합니다.
            */
            return binary_search(start, mid - 1, array, num);
        }
    }
    else{
        /*
    	중요2. (언제 끝나야할지를 몰라서)
        
        시작 인덱스 start가 마지막 인덱스 end보다 커졌는데 못찾으면 종료합니다.
        */
    	return -1;
    }
}

int main(){
    int a[10] = {1, 3, 4, 5, 7, 8, 9, 10, 11, 12};
 
    printf("%d\n", binary_search(0, 9, a, 5));
}

재귀를 쓰면 좋은점이 많아요.

1. 코드가 간단해집니다.

반복문을 사용할때 보다 코드가 더욱 간단해지는 경향이 있습니다.

2. 덜 계산합니다.(조금더 빨라집니다.)

DP를 풀때 반복문을 사용하면 모든 문제를 풀어야하는데, 재귀로 풀면 모든 문제를 안 풀어도 됩니다.

DP를 푸는 법은 크게 2가지 입니다.
1) 반복문(bottom-up, tabulation)
2) 재귀(top-down, memoization)

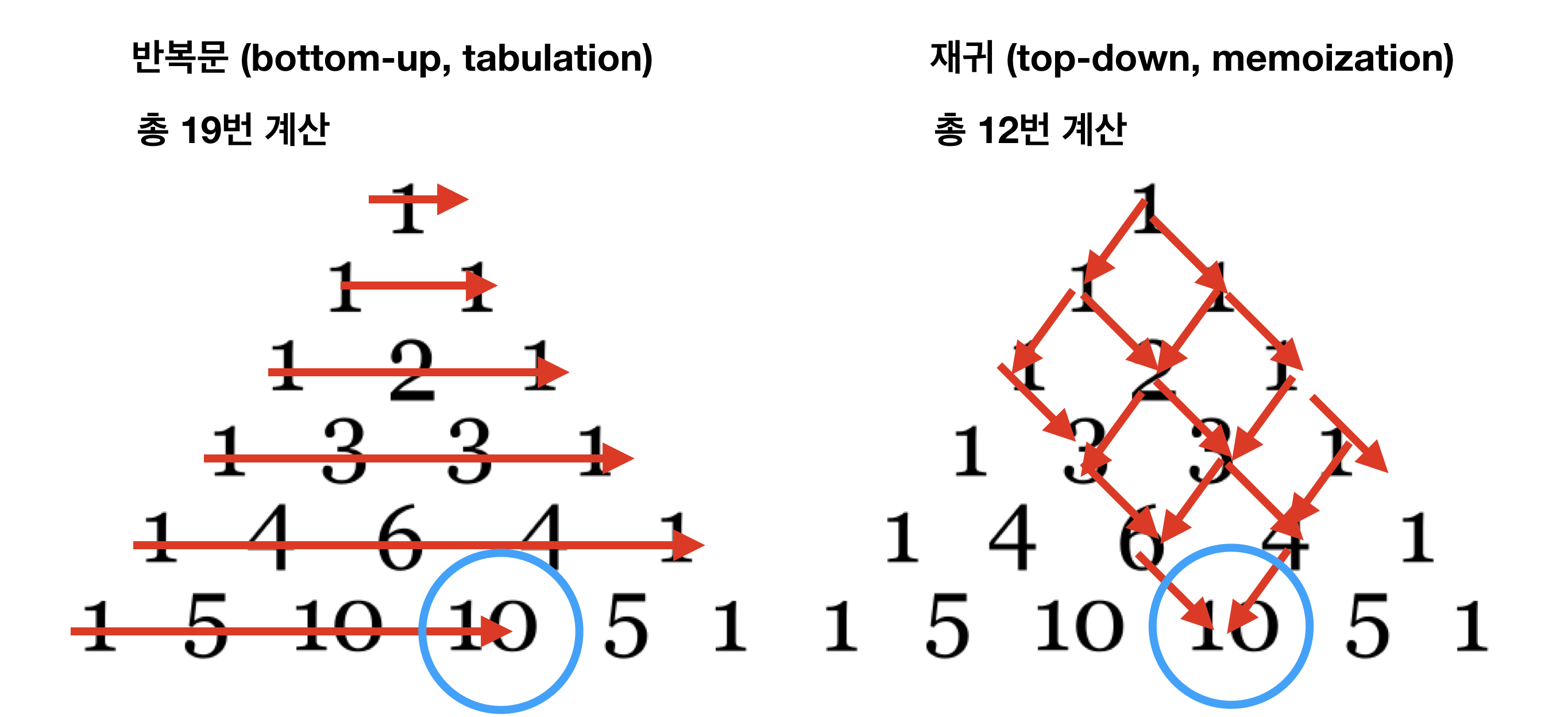
tabulation은 그 의미가 영어로 '표' 즉, 모든 표를 채우는 방법입니다.
따라서, 반복문을 사용하면 모든 표를 다 채워야해요.

하지만, 재귀를 사용하면 필요한 부분만 계산해도 됩니다.(예: 파스칼의 삼각형 - 이항계수 계산)

3. 스택을 안 사용해도 됩니다.

재귀는 내부적으로 스택을 사용합니다. 굳이 스택을 안사용해도 됩니다.
예를 들면 DFS(깊이 우선 탐색)을 스택으로 풀 수 있는데요, 보통 재귀로 짜잖아요. 일반화는 아니지만, 뭐 대부분.

일단, 재귀가 내부적으로 스택을 사용하기 때문에 굳이 스택을 안써요.

그리고,
스택으로 짜는게 더 힘들어요. 재귀는 코드가 더 간결해집니다.