주어진 이미지 분석
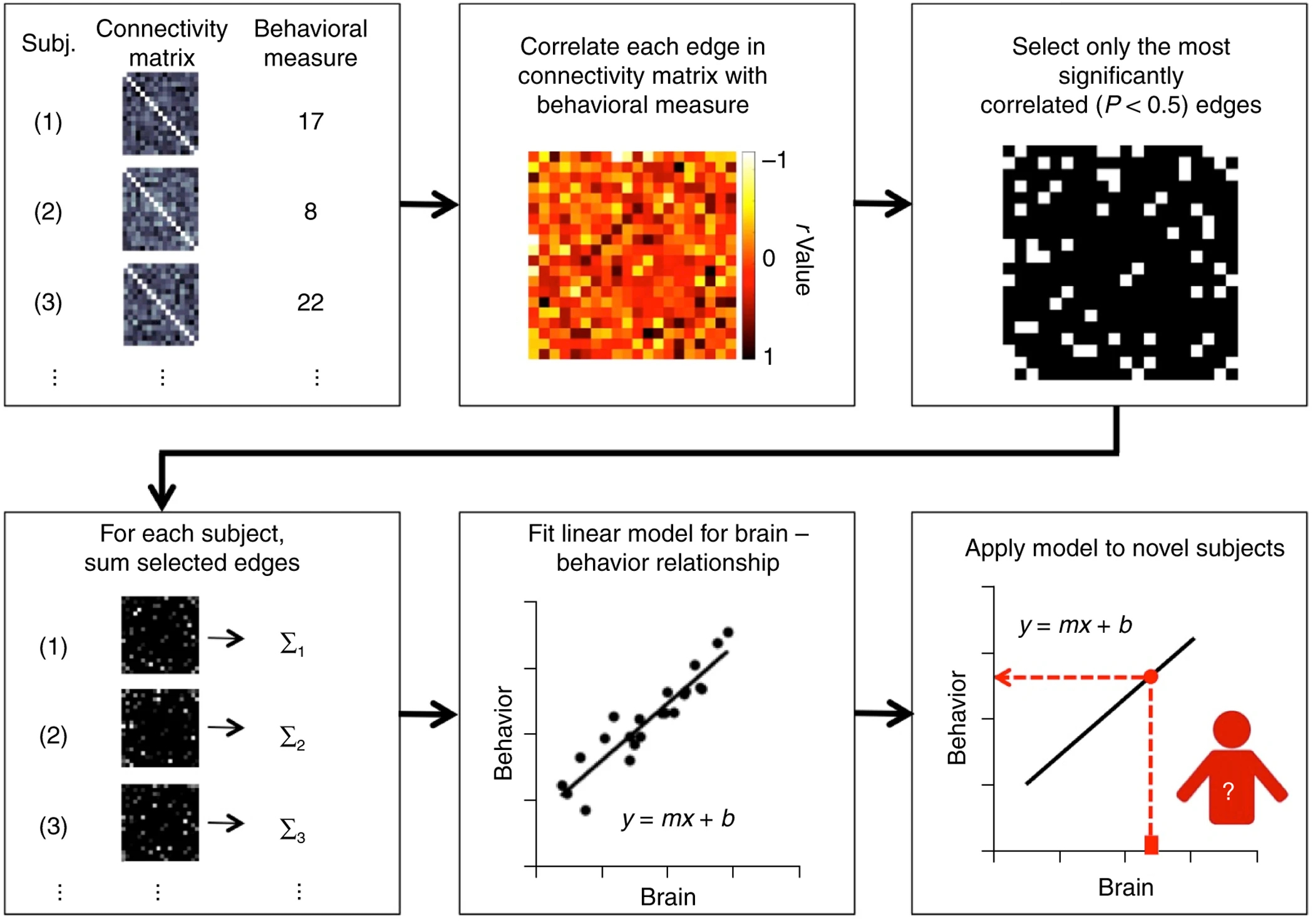
뇌 연결성과 행동 측정 간의 상관 관계를 분석하고 예측하는 과정을 나타냄
-
Subj, Connectivity matrix, Behavioral measure:
- 여러 참가자들의 뇌 연결성 매트릭스와 각각의 행동 측정 값 나타냄
- 뇌 연결성 매트릭스는 다양한 패턴의 그래픽으로 표현됨 → Connectivity matrix
- 행동 측정 값은 숫자로 주어짐 → Behavioral measure
-
Correlate each edge in connectivity matrix with behavioral measure:
- 뇌 연결성 매트릭스의 각 엣지와 행동 측정 값간 상관관계 분석
- 상관관계는 열 지도로 시각화, 다양한 색상 사용
-
Select only the most significantly correlated (P<0.5) edges:
- 가장 유의미하게 상관된 엣지만을 선택
- 선택된 엣지들은 검은색과 하얀색으로 이루어진 그래픽으로 나타남
-
For each subject, sum selected edges:
- 각 참가자에 대한 선택된 엣지 합산
- 합산된 결과는 검은색과 하얀색 그래픽으로 표시
-
Fit linear model for brain – behavior relationship:
- 뇌와 행동 간의 선형 모델 만듦
- 점과 선으로 이루어진 그래프로, 뇌와 행동 사이의 관계를 시각적으로 나타냄
-
Apply model to novel subjects:
- 새로운 참가자에 대해 모델 적용
뇌 연결성 매트릭스와 IQ값 시뮬레이션
++
조건 : 10명의 참가자 중 9명을 훈련 데이터로, 1명을 테스트 데이터로 사용
조건에 따라 코드 작성
조건
1. 10명의 사람
2. 각 사람은 하나의 행동 메이저를 가짐
3. 각 사람마다 하나의 아이큐 점수 가짐
4. 100x100 크기의 연결성 행렬 → 이미지 1번
5. 연결성 행렬은 랜덤함수를 사용하여 생성
6. 9명의 사람으로 모델 만들고, 이 중 하나로 테스트 → 5번까지는 9명으로 모델링
7. 나머지 1명은 테스트
#1. Connectivity matrix, Behavioral measure
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
# 10명의 참가자
num_participants = 10
# 뇌 연결성 매트릭스의 크기
matrix_size = 100
# 데이터 저장을 위한 리스트 초기화
connectivity_matrices = []
behavioral_measures = []
# 각 참가자별 뇌 연결성 매트릭스와 행동 측정 값을 생성
for i in range(num_participants):
# 랜덤한 연결성 행렬 생성
connectivity_matrix = np.random.rand(matrix_size, matrix_size)
connectivity_matrices.append(connectivity_matrix)
# 행동 측정 값을 생성
behavioral_measure = np.random.randint(50, 150)
behavioral_measures.append(behavioral_measure)
# 데이터를 훈련 세트와 테스트 세트로 분할 (9명 훈련, 1명 테스트)
X_train, X_test, y_train, y_test = train_test_split(connectivity_matrices, behavioral_measures, test_size=1/num_participants, random_state=42)
# 훈련 세트 시각화 및 행동 측정 값 출력
for i in range(len(X_train)):
plt.imshow(X_train[i], cmap='viridis', interpolation='nearest')
plt.title(f'Train Participant {i+1}: Connectivity Matrix')
plt.colorbar()
plt.show()
print(f'Train Participant {i+1}: Behavioral Measure - {y_train[i]}\n')
# 테스트 세트 시각화 및 행동 측정 값 출력
for i in range(len(X_test)):
plt.imshow(X_test[i], cmap='viridis', interpolation='nearest')
plt.title('Test Participant: Connectivity Matrix')
plt.colorbar()
plt.show()
print('Test Participant: Behavioral Measure -', y_test[i])
#1. 출력결과
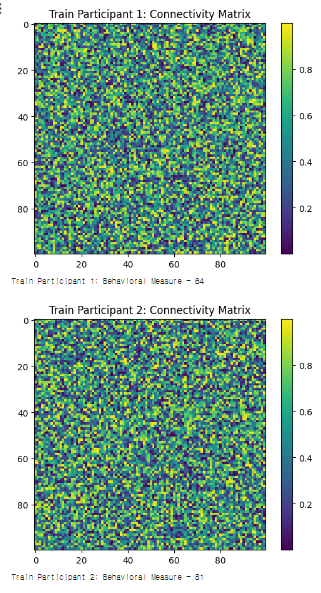
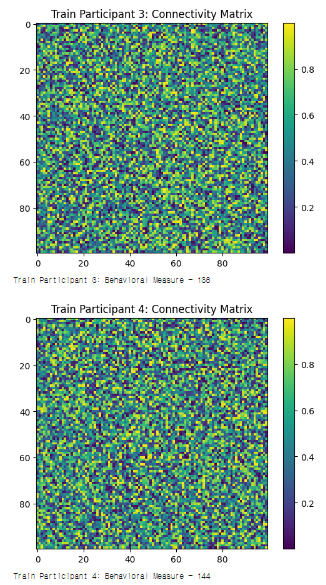
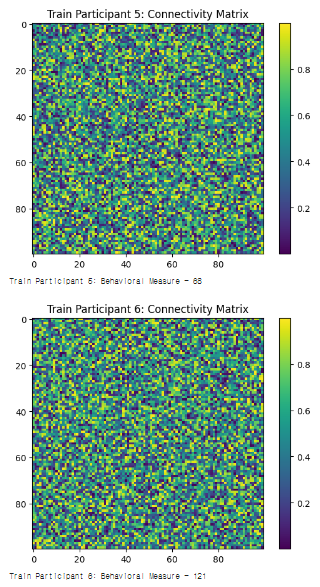

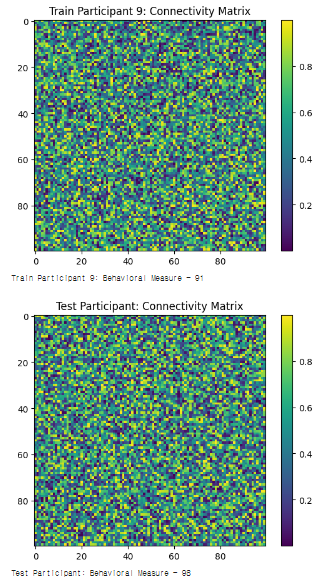
#1. 설명
- 모든 참가자의 뇌 연결성 매트릭스와 행동 측정 값을 생성하여 리스트에 저장
- train_test_split 함수를 사용하여 이 리스트를 훈련 세트와 테스트 세트로 분할
test_size=1/num_participants는 전체 데이터 중에서 하나만 테스트 데이터로 설정하겠다는 의미- 분할된 데이터를 훈련 세트와 테스트 세트로 구분하여 시각화하고 행동 측정 값을 출력
#2. Correlate each edge in connectivity matrix with behavioral measure:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns #seaborn은 파이썬에서 데이터 시각화를 위한 라이브러리
from sklearn.model_selection import train_test_split
# 참가자 수와 뇌 연결성 매트릭스 크기 설정
num_participants = 10
matrix_size = 10 # 예시로 크기를 10으로 설정;
# 랜덤한 연결성 매트릭스 생성 (각 참가자별)
np.random.seed(42) # 결과의 일관성을 위해 시드 설정
connectivity_matrices = np.random.rand(num_participants, matrix_size, matrix_size)
# 행동 측정 값
behavioral_measures = np.array([94, 149, 149, 65, 129, 63, 51, 104, 143, 78])
# 데이터를 훈련 세트와 테스트 세트로 분할 (9명 훈련, 1명 테스트)
X_train, X_test, y_train, y_test = train_test_split(connectivity_matrices, behavioral_measures, test_size=1/num_participants, random_state=42)
# 각 엣지와 행동 측정 값간 상관관계 저장을 위한 배열 초기화 (훈련 데이터에 대해서만)
correlations = np.zeros((matrix_size, matrix_size))
# 각 엣지에 대해 훈련 데이터의 행동 측정 값과의 상관관계 계산
for i in range(matrix_size):
for j in range(matrix_size):
edge_values = X_train[:, i, j]
correlation = np.corrcoef(edge_values, y_train)[0, 1]
correlations[i, j] = correlation
# 상관관계 열 지도로 시각화 (훈련 데이터에 대해서만)
plt.figure(figsize=(10, 8))
ax = sns.heatmap(correlations, cmap='coolwarm', center=0, annot=True, fmt=".2f")
plt.title('Correlation between Connectivity Edges and Behavioral Measures (Train Data)')
plt.xlabel('Brain Region A')
plt.ylabel('Brain Region B')
# 컬러바 라벨 설정
ax.figure.colorbar(ax.collections[0]).set_label('Correlation Coefficient')
plt.show()
#2. 출력결과
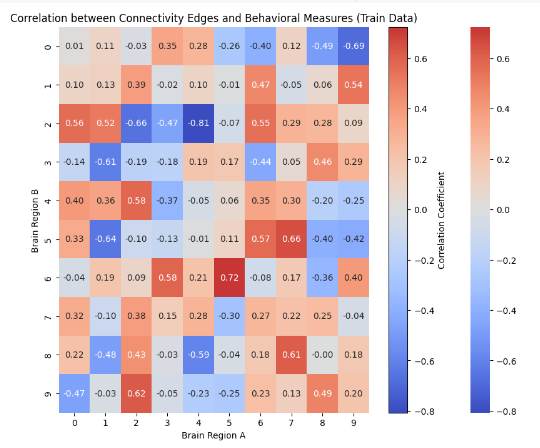
#2. 설명
- 전체 데이터를 훈련 데이터와 테스트 데이터로 분할
* 훈련 데이터에 대해서만 각 뇌 영역(엣지) 사이의 연결성과 행동 측정 값 간의 상관관계를 계산하고, heatmap으로 시각화
#3. Select only the most significantly correlated (P<0.5) edges:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 참가자 수와 뇌 연결성 매트릭스 크기 설정
num_participants = 10
matrix_size = 10 # 예시로 크기를 10으로 설정
# 랜덤한 연결성 매트릭스 생성 (각 참가자별)
np.random.seed(42) # 결과의 일관성을 위해 시드 설정
connectivity_matrices = np.random.rand(num_participants, matrix_size, matrix_size)
# 행동 측정 값
behavioral_measures = np.array([94, 149, 149, 65, 129, 63, 51, 104, 143, 78])
# 훈련 데이터와 테스트 데이터 분리
# 마지막 참가자를 테스트 데이터로 사용
train_data = connectivity_matrices[:-1]
test_data = connectivity_matrices[-1]
train_behavior = behavioral_measures[:-1]
# 각 엣지와 행동 측정 값 간 상관관계 저장을 위한 배열 초기화 (훈련 데이터에 대해서만)
correlations = np.zeros((matrix_size, matrix_size))
# 훈련 데이터에 대해 각 엣지와 행동 측정 값 간 상관관계 계산
for i in range(matrix_size):
for j in range(matrix_size):
edge_values = train_data[:, i, j]
correlation = np.corrcoef(edge_values, train_behavior)[0, 1]
correlations[i, j] = correlation
# 유의미한 상관관계를 가지는 엣지만 선택 (상관관계의 절대값이 0.5 이상인 경우) -> p<0.5
significant_correlations = np.where(np.abs(correlations) >= 0.5, 1, 0)
# 유의미한 상관관계를 가지는 엣지 시각화 (훈련 데이터 기반)
plt.figure(figsize=(10, 8))
sns.heatmap(significant_correlations, cmap='binary', cbar=False, annot=True, fmt="d")
plt.title('Significant Correlation between Connectivity Edges and Behavioral Measures (Train Data)')
plt.xlabel('Brain Region A')
plt.ylabel('Brain Region B')
plt.show()
#3. 출력결과
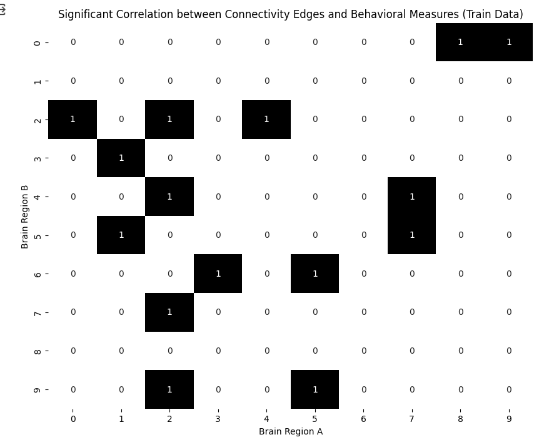
#3. 설명
- 유의미한 상관관계(P<0.5)를 가지는 엣지만 선택하는 부분을, 상관관계의 절대값이 0.5 이상인 경우를 기준으로 설정
- P-value를 계산하고 필터링하는 기능은 포함하지 않아, 추가적인 통계 함수 사용해 구현
#4. For each subject, sum selected edges:
import numpy as np
import matplotlib.pyplot as plt
# 참가자 수와 뇌 연결성 매트릭스 크기 설정
num_participants = 10
matrix_size = 10
# 랜덤한 연결성 매트릭스 생성 (각 참가자별)
np.random.seed(42)
connectivity_matrices = np.random.rand(num_participants, matrix_size, matrix_size)
# 훈련 데이터와 테스트 데이터 분리
# 마지막 참가자를 테스트 데이터로 사용
train_data = connectivity_matrices[:-1]
test_data = connectivity_matrices[-1]
# 유의미한 상관관계를 가지는 엣지 선택 (상관관계의 절대값이 0.5 이상인 경우)
significant_correlations = np.random.choice([0, 1], size=(matrix_size, matrix_size))
# 훈련 데이터에 대해 유의미한 엣지의 값을 합산
summed_edges_per_subject = np.array([np.sum(matrix * significant_correlations) for matrix in train_data])
# 합산된 결과를 바탕으로 훈련 데이터의 참가자를 검은색(낮은 값)과 하얀색(높은 값)으로 구분하기 위한 이진화
median_value = np.median(summed_edges_per_subject)
binary_summed_edges = np.where(summed_edges_per_subject > median_value, 1, 0)
# 훈련 데이터 참가자별로 합산된 결과 시각화
plt.figure(figsize=(12, 6))
plt.imshow(binary_summed_edges.reshape(1, len(train_data)), cmap='binary') # 훈련 데이터 참가자 수만큼 조정
plt.colorbar(ticks=[0, 1], aspect=10)
plt.title("Summed Selected Edges for Each Subject (Train Data)")
plt.yticks([])
plt.xticks(range(len(train_data)), [f"Subject {i+1}" for i in range(len(train_data))])
plt.show()
# 테스트 데이터에 대해 유의미한 엣지의 값을 합산
summed_edges_test_subject = np.sum(test_data * significant_correlations)
# 테스트 데이터의 결과를 이진화
binary_summed_edges_test = 1 if summed_edges_test_subject > median_value else 0
# 테스트 데이터의 결과 시각화
plt.figure(figsize=(3, 2))
plt.imshow(np.array([[binary_summed_edges_test]]), cmap='binary')
plt.colorbar(ticks=[0, 1], aspect=10)
plt.title("Summed Selected Edges for Test Subject")
plt.yticks([])
plt.xticks([])
plt.show()
#4. 출력결과

#4. 설명
- 각 참가자에 대해 유의미한 엣지의 값을 합산하는 과정을 훈련 데이터에 대해서만 수행
- 얻은 결과를 테스트 데이터에 적용하여 시각화
#5. Fit linear model for brain – behavior relationship:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 참가자별 선택된 엣지들의 합산값
summed_edges_per_subject = np.random.rand(10)
# 행동 측정값 (1에서 생성한 랜덤값)
behavioral_measures = np.array([94, 149, 149, 65, 129, 63, 51, 104, 143, 78])
# 훈련 데이터와 테스트 데이터 분리
# 여기서는 마지막 참가자를 테스트 데이터로 사용합니다.
X_train = summed_edges_per_subject[:-1].reshape(-1, 1)
y_train = behavioral_measures[:-1]
X_test = summed_edges_per_subject[-1].reshape(-1, 1)
y_test = behavioral_measures[-1]
# 선형 모델 적합 (훈련 데이터에 대해서만)
model = LinearRegression().fit(X_train, y_train)
# 예측값 계산 (훈련 데이터에 대해서)
y_pred_train = model.predict(X_train)
# 뇌와 행동 사이의 관계를 나타내는 그래프 생성 (훈련 데이터에 대해서)
plt.figure(figsize=(10, 6))
plt.scatter(X_train, y_train, color='blue', label='Actual data') # 실제 데이터 포인트
plt.plot(X_train, y_pred_train, color='red', label='Linear model') # 선형 모델
plt.title("Brain Connectivity - Behavioral Measure Relationship (Train Data)")
plt.xlabel("Summed Edges")
plt.ylabel("Behavioral Measure")
plt.legend()
plt.show()
# 테스트 데이터에 대한 예측 수행 및 결과 출력
y_pred_test = model.predict(X_test)
print("테스트 데이터 예측값:", y_pred_test)
print("테스트 데이터 실제값:", y_test)
#5. 출력결과
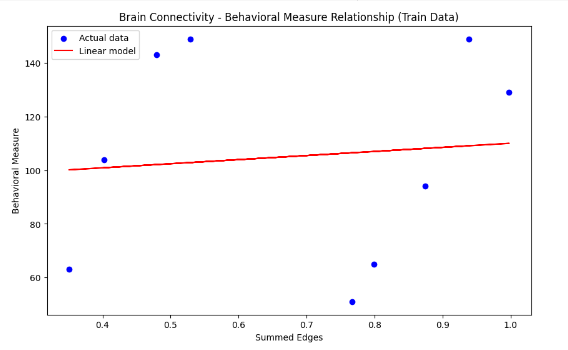
#5. 설명
- 훈련 데이터를 사용하여 선형 회귀 모델을 적합
- 훈련 데이터에 대한 예측을 수행
- 테스트 데이터에 대한 예측값과 실제값을 출력하여 모델의 성능을 평가
#6. Apply model to novel subjects:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 참가자별 선택된 엣지들의 합산값
summed_edges_per_subject = np.random.rand(10)
# 행동 측정값
behavioral_measures = np.array([94, 149, 149, 65, 129, 63, 51, 104, 143, 78])
# 훈련 데이터와 테스트 데이터 분리
# 9명을 훈련 데이터로, 1명을 테스트 데이터로 사용
X_train = summed_edges_per_subject[:-1].reshape(-1, 1)
y_train = behavioral_measures[:-1]
# 새로운 참가자들의 뇌 연결성 데이터 (선택된 엣지들의 합산값)
# 랜덤 데이터 사용
new_summed_edges = np.random.rand(5)
X_new = new_summed_edges.reshape(-1, 1)
# 훈련 데이터에 대해서만 선형 모델 적합
model = LinearRegression().fit(X_train, y_train)
# 새로운 참가자들에 대한 행동 측정값 예측
y_new_pred = model.predict(X_new)
# 그래프 생성
plt.figure(figsize=(10, 6))
# 훈련 데이터에 대한 원래 참가자들의 데이터
plt.scatter(X_train, y_train, color='blue', label='Training Subjects')
# 새로운 참가자들의 예측 데이터
plt.scatter(X_new, y_new_pred, color='green', label='Novel Subjects Predictions')
# 적합한 선형 모델
# 훈련 데이터와 새로운 데이터를 결합하여 모델을 시각화
X_combined = np.concatenate((X_train.squeeze(), new_summed_edges))
y_combined_pred = model.predict(X_combined.reshape(-1, 1))
plt.plot(np.sort(X_combined), np.sort(y_combined_pred), color='red', label='Linear Model')
plt.title("Brain Connectivity - Behavioral Measure Relationship with Novel Subjects")
plt.xlabel("Summed Edges")
plt.ylabel("Behavioral Measure")
plt.legend()
plt.show()
#6. 출력결과
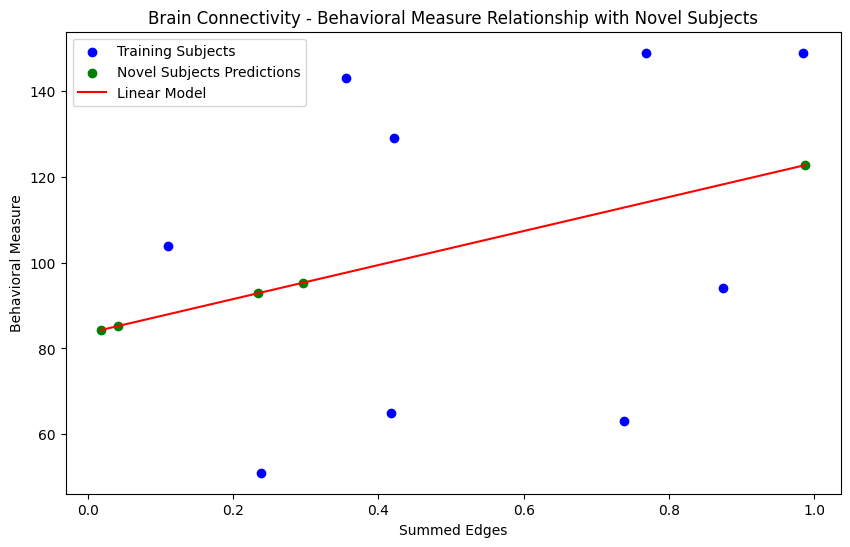
#6. 설명
- 10명의 참가자 중 9명을 사용하여 선형 회귀 모델을 훈련
- 새로운 5명의 참가자에 대해 해당 모델을 사용하여 행동 측정값을 예측
- 그래프 : 훈련 데이터에 대한 원래 참가자들의 데이터, 새로운 참가자들의 예측 데이터, 그리고 이 두 데이터를 기반으로 한 선형 모델을 시각화
데이터를 훈련과 테스트로 분리하여 모델의 일반화 능력을 평가하는 과정 구현
* 출처
Yoo K, Rosenberg MD, Kwon YH, Scheinost D, Constable RT, Chun MM. A cognitive state transformation model for task-general and task-specific subsystems of the brain connectome. NeuroImage. 2022 Aug; 257: 119279. [DOI: 10.1016/j.neuroimage.2022.119279]. MATLAB Toolbox. (2022 IF: 5.7; Neuroimaging Top 7.1%, rank 1/14)
