machine learning - intro : 데이터 취업 스쿨 스터디 노트 1/15

What is Machine Learning?
과거 데이터로부터 얻은 경험이 쌓여 감에 따라 주어진 Task의 성능이 점점 좋아질 때 컴퓨터 프로그램이 경험으로부터 학습한다고 할 수 있다.

1. 데이터 관찰

• iris 품종 분류 : setosa(0), versicolor(1), virginica(2)
• sepal : 꽃받침
• petal : 꽃잎

from sklearn.datasets import load_iris

# iris 데이터 가져오기
iris = load_iris()

# 데이터 확인
iris.keys()

iris.target_names
iris["target_names"]

iris.feature_names

import pandas as pd

iris_pd = pd.DataFrame(iris.data, columns=iris.feature_names)
iris_pd["species"] = iris.target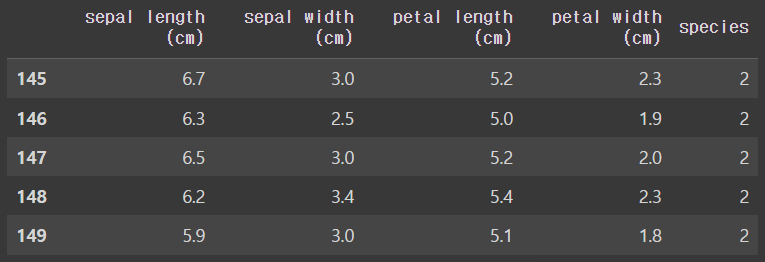

import seaborn as sns
import matplotlib.pyplot as plt

plt.figure(figsize=(12, 6))
sns.boxplot(x='sepal length (cm)', y='species', data=iris_pd, orient='h');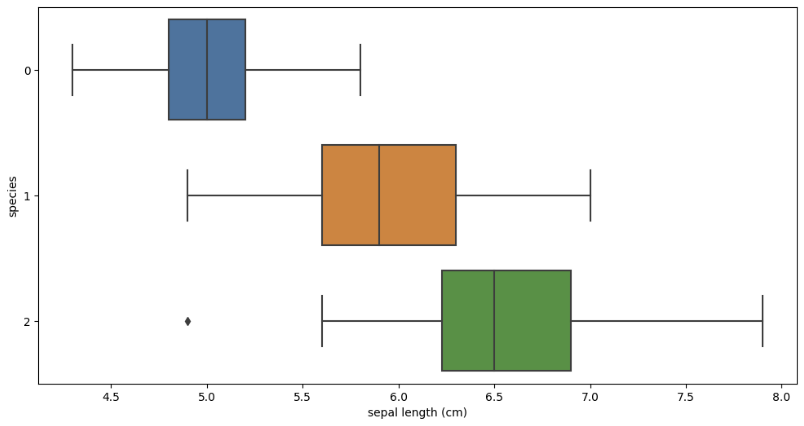

세 품종이 모두 겹치는 구간이 있기 때문에 sepal length만으로 구분할 수 없다. 이상치도 확인된다.

plt.figure(figsize=(12, 6))
sns.boxplot(x='sepal width (cm)', y='species', data=iris_pd, orient='h');

plt.figure(figsize=(12, 6))
sns.boxplot(x='petal length (cm)', y='species', data=iris_pd, orient='h');

plt.figure(figsize=(12, 6))
sns.boxplot(x='petal width (cm)', y='species', data=iris_pd, orient='h');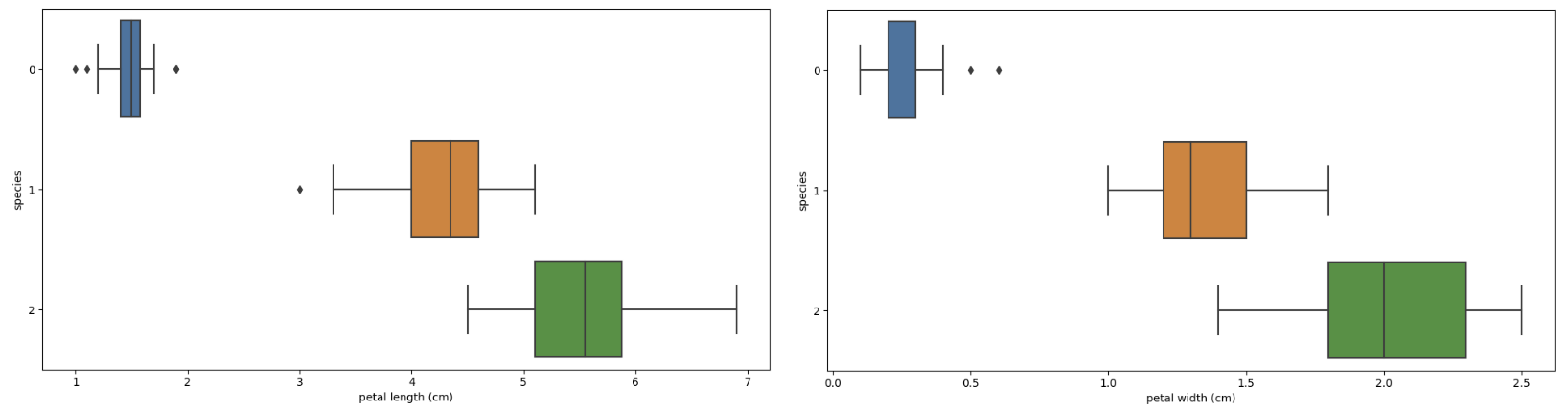

setosa(0)는 명확하게 구분된다.

sns.pairplot(iris_pd, hue='species');

# 눈에 띄는 특성만 골라서 다시 확인
sns.pairplot(data=iris_pd,
             vars=['petal length (cm)', 'petal width (cm)'],
             hue='species',
             height=4);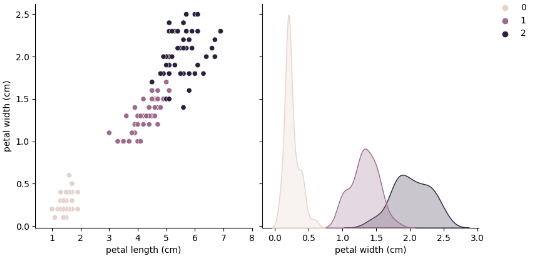

2. Decision Tree

plt.figure(figsize=(12, 6))
sns.scatterplot(x='petal length (cm)', y='petal width (cm)',
                data=iris_pd, hue='species', palette='Set2');
                
# 1, 2만 자세히 보기
iris_12 = iris_pd[iris_pd['species']!=0]
plt.figure(figsize=(12, 6))
sns.scatterplot(x='petal length (cm)', y='petal width (cm)',
                data=iris_12, hue='species', palette='Set2');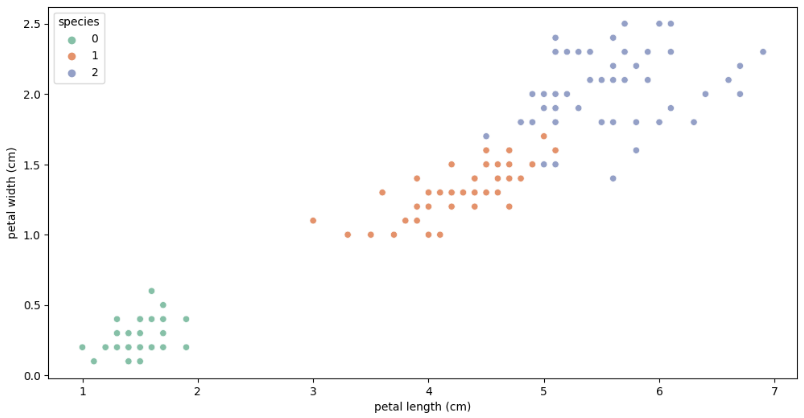

versicolor(1), virginica(2)를 구분하는 선을 어떻게 찾을까?

지도 학습 : 정답 알려주고 학습 시키기

• features = petal length, petal width
• label = species
• data(features + label) ➡ model [학습]
• new_data(features) ➡ model ➡ predict ➡ (label) [추론]

from sklearn.tree import DecisionTreeClassifier

iris_tree = DecisionTreeClassifier()

# fit(): 데이터와 정답을 주고 학습 시키기
iris_tree.fit(iris.data[:, 2:], iris.target)

from sklearn.metrics import accuracy_score

# 학습한 iris_tree에 예측 시키기(정답 제외, 데이터만 제공)
y_pred_tr = iris_tree.predict(iris.data[:, 2:])
accuracy_score(iris.target, y_pred_tr)

>>>
0.9933333333333333

과적합(overfitting)

from sklearn.tree import plot_tree

# iris_tree 구조 확인
plt.figure(figsize=(12, 8))
plot_tree(iris_tree);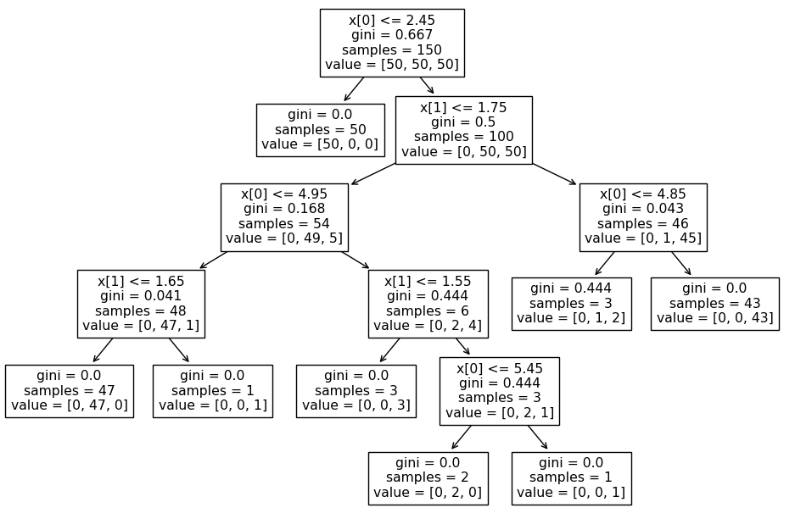

from mlxtend.plotting import plot_decision_regions

# iris_tree 모델이 어떻게 데이터를 분류했는지 확인하기
plt.figure(figsize=(14, 8))
plot_decision_regions(X=iris.data[:, 2:], y=iris.target,
                      clf=iris_tree, legend=2)
plt.show()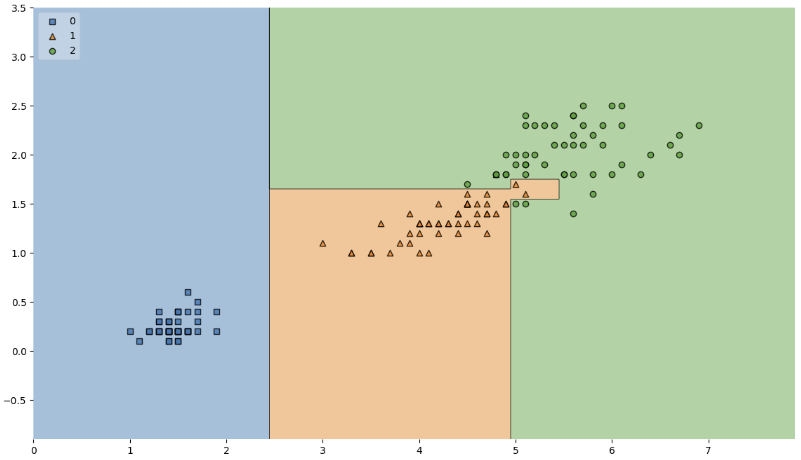

경계면이 적절한 것일까?
내가 가진 데이터를 벗어나서 일반화할 수 있을까?

복잡한 경계면은 오히려 모델의 성능을 나쁘게 만들 수 있다.
내가 가진 데이터에 너무 적합하면 일반적인 iris 데이터에 대해서는 좋은 성능을 가지기 어렵다.

데이터 나누기 : train, test

150개 데이터를 두 세트로 나눠서 한 세트로만 학습시킨 후 다른 세트로 테스트하여 모델이 잘 예측하는지 확인해보자.

from sklearn.model_selection import train_test_split

features = iris.data[:, 2:]
labels = iris.target

X_train, X_test, y_train, y_test = train_test_split(
    features, labels, test_size=0.2, random_state=13
)

X_train.shape, X_test.shape

>>>
((120, 2), (30, 2))

train, test가 잘 분리되었을까?
class가 여러 개일수록 각 class별 분포를 반드시 확인해야 한다.

import numpy as np

np.unique(y_test, return_counts=True)

>>>
(array([0, 1, 2]), array([ 9,  8, 13]))

stratify 옵션을 이용해서 class 비율을 맞춰준다.

X_train, X_test, y_train, y_test = train_test_split(
    features, labels, test_size=0.2, stratify=labels, random_state=13
)

np.unique(y_test, return_counts=True)

>>>
(array([0, 1, 2]), array([10, 10, 10]))

train 세트로 학습시키기

# max_depth 옵션으로 성능 제한 [규제]
iris_tree = DecisionTreeClassifier(max_depth=2, random_state=13)
iris_tree.fit(X_train, y_train)
y_pred_tr = iris_tree.predict(X_train)
accuracy_score(y_train, y_pred_tr)

>>>
0.95

plt.figure(figsize=(12, 8))
plot_tree(iris_tree);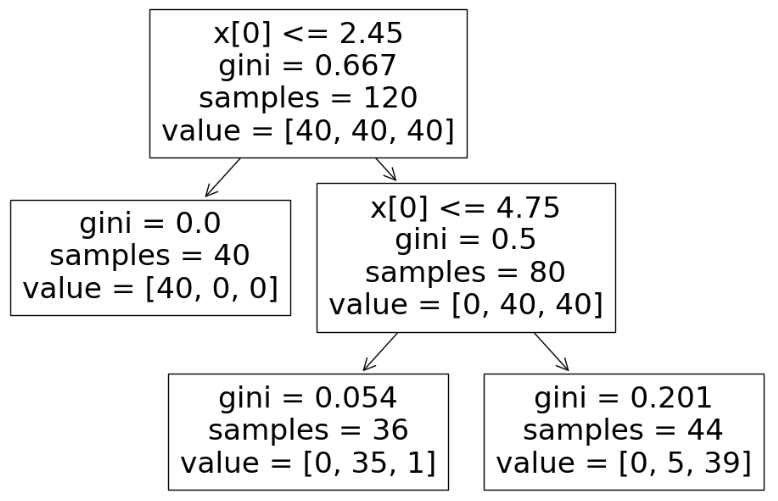

plt.figure(figsize=(12, 8))
plot_decision_regions(X=X_train, y=y_train, clf=iris_tree, legend=2)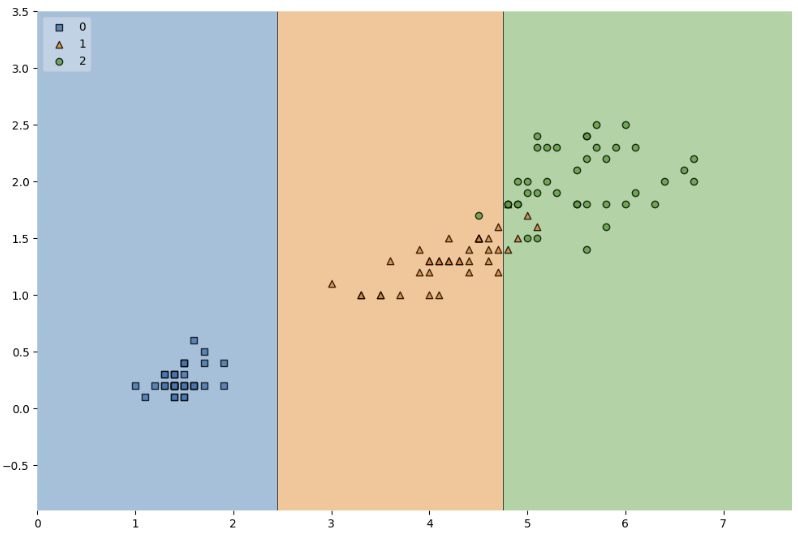

테스트 데이터에 대한 정확도를 확인한다.

y_pred_test = iris_tree.predict(X_test)
accuracy_score(y_test, y_pred_test)

>>>
0.9666666666666667

# 마커의 특성 : 사이즈, 라벨, 투명도
scatter_highlight_kwargs = {'s': 150,
                            'label': 'Test data',
                            'alpha': 0.9}

scatter_kwargs = {'s': 120,
                  'edgecolor': None,
                  'alpha': 0.9}

plt.figure(figsize=(12, 8))
plot_decision_regions(X=features, y=labels,
                      X_highlight=X_test,
                      clf=iris_tree,
                      legend=2,
                      scatter_highlight_kwargs=scatter_highlight_kwargs,
                      scatter_kwargs=scatter_kwargs,
                      contour_kwargs={'alpha': 0.2})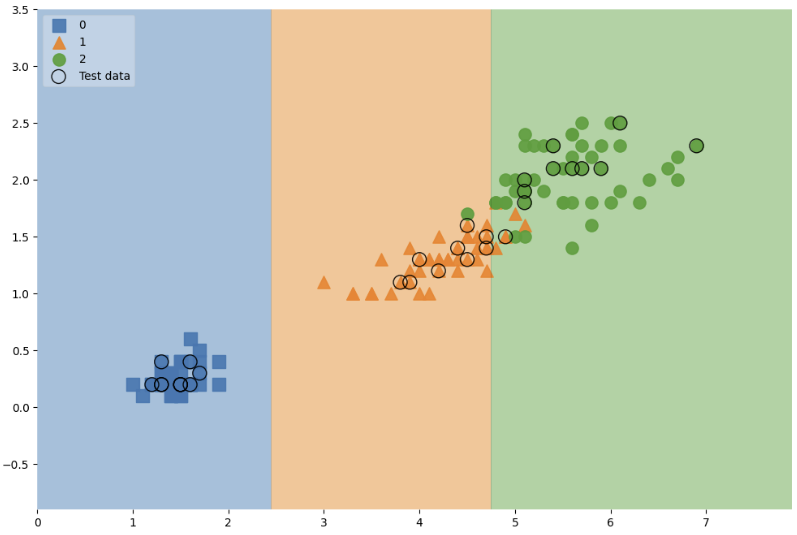

feature 개수를 4개로 늘리면?

features = iris.data
labels = iris.target

X_train, X_test, y_train, y_test = train_test_split(
    features, labels, test_size=0.2, stratify=labels, random_state=13
)

iris_tree = DecisionTreeClassifier(max_depth=2, random_state=13)
iris_tree.fit(X_train, y_train)

plt.figure(figsize=(12, 8))
plot_tree(iris_tree);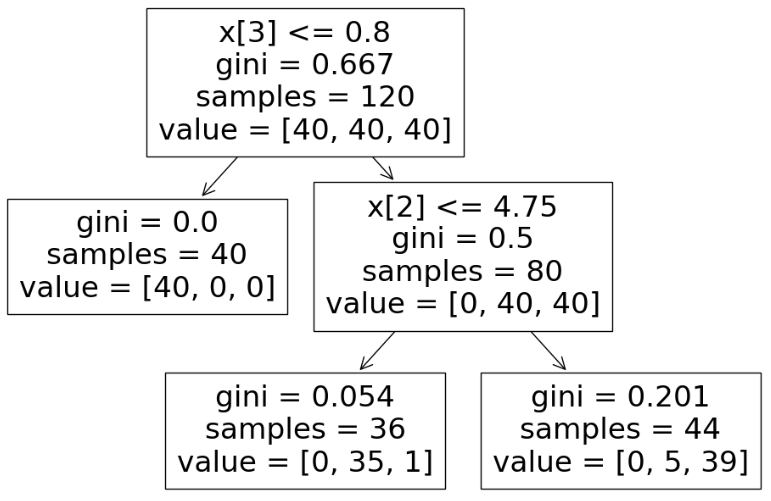

새로운 데이터로 테스트하기

연산이 가능하도록 shape를 잡아주는 게 중요하다.

np.array([4.3, 2., 1.2, 1.]).shape # (4, )
np.array([[4.3, 2., 1.2, 1.]]).shape # (1, 4)

test_data = np.array([[4.3, 2., 1.2, 1.]])
iris_tree.predict(test_data)
iris_tree.predict_proba(test_data)

>>>
array([[0.        , 0.97222222, 0.02777778]])

iris.target_names[iris_tree.predict(test_data)]

>>>
array(['versicolor'], dtype='<U10')

iris_tree.feature_importances_

>>>
array([0.        , 0.        , 0.42189781, 0.57810219])

dict(zip(iris.feature_names, iris_tree.feature_importances_))

>>>
{'sepal length (cm)': 0.0,
 'sepal width (cm)': 0.0,
 'petal length (cm)': 0.421897810218978,
 'petal width (cm)': 0.578102189781022}

엔트로피, 지니계수

엔트로피

• 어떤 확률 분포로 일어나는 사건을 표현하는 데 필요한 정보의 양
• 엔트로피가 커질수록 확률분포의 불확실성이 커져서 결과 예측이 어려워진다.

# p: 데이터가 어떤 클래스에 속할 확률
p = np.arange(0.001, 1, 0.001)
plt.plot(p, -p*np.log2(p));
plt.grid()
plt.title("$-p \log_{2}{p}$");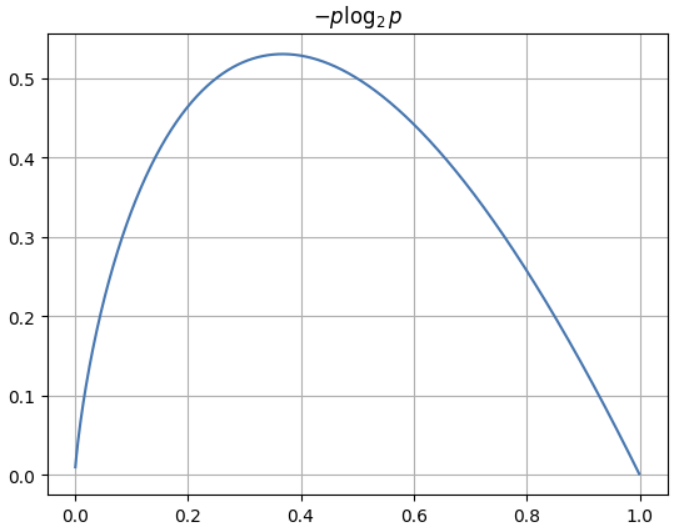

# 빨간공 10개, 파란공 6개
-(10/16)*np.log2(10/16) - (6/16)*np.log2(6/16) # 0.954434002924965

# 빨간공 7개, 파란공 1개 & 빨간공 3개, 파란공 5개
0.5 * (-(7/8)*np.log2(7/8) - (1/8)*np.log2(1/8)) \
+ 0.5 * (-(3/8)*np.log2(3/8) - (5/8)*np.log2(5/8)) # 0.7489992230622807

분할 후 엔트로피가 내려갔기 때문에 분할하는 게 좋다.
엔트로피는 계산량이 많다는 단점이 있어서, 비슷한 개념이면서 계산량이 적은 지니계수(불순도율)를 사용하는 경우가 많다.

# 빨간공 10개, 파란공 6개
1 - (10/16)**2 - (6/16)**2 # 0.46875

# 빨간공 7개, 파란공 1개 & 빨간공 3개, 파란공 5개
0.5 * (1 - (7/8)**2 - (1/8)**2) + 0.5 * (1 - (3/8)**2 - (5/8)**2) # 0.34375

zip - unpacking

list1 = ['a', 'b', 'c']
list2 = [1, 2, 3]

pairs = [pair for pair in zip(list1, list2)]
pairs

>>>
[('a', 1), ('b', 2), ('c', 3)]

dict(pairs)

>>>
{'a': 1, 'b': 2, 'c': 3}

아래와 같이 간단하게 딕셔너리로 묶을 수도 있다.

dict(zip(list1, list2))

>>>
{'a': 1, 'b': 2, 'c': 3}

다시 리스트 형태로 돌려 놓으려면 (unpacking)

x, y = zip(*pairs)
list(x)

>>>
['a', 'b', 'c']