개발자를 위한 머신러닝&딥러닝 Ch2. 컴퓨터 비전 소개

개념 이해하기

손글씨를 신경망에 학습시키기 위해 사용하는 기초적인 데이터셋 중 가장 유명한 것은 MNIST(Modified National Institute of Standards and Technology) 데이터셋인데, 이 장에서는 10종 의류의 흑백 샘플 사진을 담은 패션 MNIST 데이터셋을 이용하여 사진을 통해 의류 아이템을 구분하는 신경망을 구현하는 것을 목표로 한다. 아래 사진이 패션 MNIST 데이터셋인데, 하나의 데이터는 $28×28$의 크기를 가지고 각각의 픽셀이 0부터 255 사이의 값을 갖는다.

1장에서는 $x$와 $y$ 값이 실수로 주어졌을 때, 즉 입력값이 하나이고 출력값이 하나일 때 관계식, 특히 $y=wx+b$ 의 관계에서 $w$와 $b$를 단일 뉴런을 통해 찾아보았다.

이번에 나온 패션 MNIST에서는, 입력으로 주어질 하나의 데이터가 $28×28=784$의 숫자로 이루어져 있고 출력은 10가지의 패션 아이템이 되므로 입력과 출력의 관계를 $y=wx+b$ 처럼 간단하게 표현할 수 없다.

하지만 하나가 아닌 여러 개의 뉴런을 사용한다면 이러한 관계도 표현할 수 있는데, 아래 그림처럼 784개의 숫자로 입력을 받고, 출력층에서는 입력받은 이미지가 각각의 패션 아이템에 해당할 확률 값이 되도록 신경망을 학습시킨 뒤, 10개의 출력 중 가장 큰 값을 최종 답으로 결정할 수 있을 것이다. 즉, 784차원 벡터를 입력받아 10차원 벡터를 출력하는 함수를 만들게 된다.

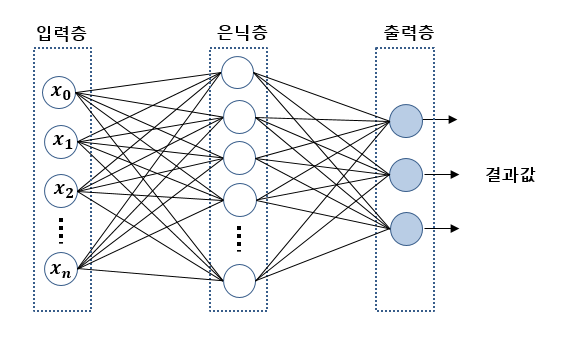
신경망은 입력층(input layer), 은닉층(hidden layer), 출력층(output layer)으로 이루어져 있는데, 이는 Sequential 클래스에 여러 개의 층을 넣어서 구현할 수 있다.

입력층과 출력층만으로는 표현하기 힘든 복잡한 관계에 대해서 학습하기 위해 은닉층을 만드는데, 은닉층의 뉴런 개수를 정하는 방법은 규칙은 아직 없지만 은닉층의 뉴런 개수가 너무 적으면 학습에 필요한 가중치와 편향 값의 개수가 적어 복잡한 관계를 학습할 수 없고, 너무 많으면 계산이 많아져 실행 속도가 느려지고 훈련에 쓰인 데이터에서만 높은 성능을 보이는 과대적합(overfitting)이 일어날 수 있다.

각 층의 뉴런에는 비선형적인 관계를 학습하고 은닉층의 효과를 극대화하기 위해 활성화 함수(activation function)이 적용되는데, 활성화 함수가 없으면 뉴런의 개수가 아무리 많아도 결국 선형적인 관계로 표현되므로 선형 관계 판별이 어려운 실제 데이터에서 유효한 학습 효과를 얻기 위해서 꼭 필요하다.

공부한 내용을 토대로 설명을 추가한 책의 예제 코드는 아래와 같다.

import tensorflow as tf

# Fashion MNIST 데이터셋 가져오기
data = tf.keras.datasets.fashion_mnist
# 가져온 데이터셋에서 일부(60,000개)는 훈련에 사용, 일부(10,000개)는 테스트에 사용
(training_images, training_labels), (test_images, test_labels) = data.load_data()

# 이미지 정규화(Tensorflow에서 학습 효과를 높이기 위함)
training_images = training_images / 255.0
test_images = test_images / 255.0

model = tf.keras.models.Sequential([
    # Flatten은 뉴런으로 구성된 층이 아니라 입력으로 주어지는 28*28 행렬을 1차원 벡터로 변환하기 위한 층
    tf.keras.layers.Flatten(input_shape=(28, 28)),
    # 은닉층, ReLU 함수는 음수는 0으로, 0과 양수는 그대로 반환하는 함수
    tf.keras.layers.Dense(128, activation=tf.nn.relu),
    # 출력층, Softmax 함수는 k차원 벡터의 값을 입력으로 받아 각 성분을 0과 1 사이의 값으로 만들어 주는 함수
    tf.keras.layers.Dense(10, activation=tf.nn.softmax)
])

# 훈련 방법 설정
model.compile(optimizer='adam',
              # 정수 레이블을 갖는 분류 문제에서 사용하는 손실 함수
              loss='sparse_categorical_crossentropy',
              # 손실뿐만 아니라 정확도를 통해서 신경망의 학습 확인
              metrics=['accuracy'])

# 훈련 시작
model.fit(training_images, training_labels, epochs=5)

# 테스트 데이터를 통해 모델의 정확성 평가
model.evaluate(test_images, test_labels)

# 첫 테스트 데이터를 신경망에 넣었을 때의 출력, 분류 결과, 정답 레이블
classifications = model.predict(test_images)
print(classifications[0])
print(list(classifications[0]).index(max(classifications[0])))
print(test_labels[0])

위 예제 코드에서 model.compile() 에 들어가는 parameter를 조금만 더 살펴보자.

model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

먼저 옵티마이저(optimizer)는, 우리가 모델을 학습시키기 위해 실제 결과와 모델이 예측한 결과의 차이, 즉 손실 함수(loss function)을 최소화하기 위하여 뉴런의 parameter를 조절하는 방법을 제시한다. 우리가 4차원 이상의 공간을 상상하지 못하기 때문에 손실 함수의 그래프를 시각적으로 나타낼 수는 없지만, 손실 함수 역시 아래 그림처럼 최솟값을 갖고, 이 값을 찾는 것이 학습의 주된 과정에 해당한다. 보통 어떤 지점에서의 기울기(gradient)가 0이 되는 지점이 최소가 되는 점의 '후보'가 되는데, 이 많은 후보들 중에 손실 함수가 '정말' 최소가 되는 지점을 찾기 위한 여러 방법이 연구되고 있으며 그 중 정확도나 성능 면에서 무난하여 가장 널리 사용되는 방법이 adam 알고리즘이다. 이외의 다른 옵티마이저에 대한 수학적인 설명은 여기에서 찾아볼 수 있다.

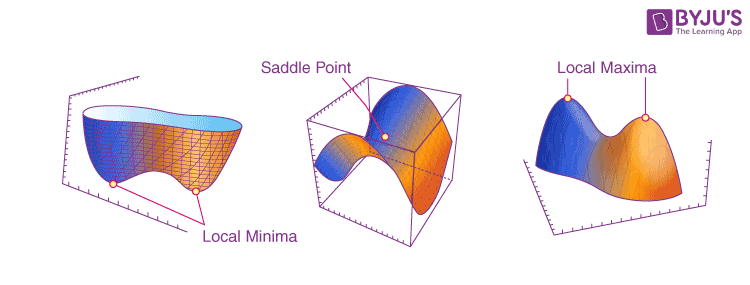
다음으로 손실 함수(loss function)는 정답의 값과 모델의 예측 값이 얼마나 차이가 나는지를 함수로 나타낸 것으로, 위에서 설명한 것처럼 이를 최소로 만드는 뉴런의 parameter를 찾는 과정을 학습이라고 볼 수 있다. 손실 함수를 정의하는 방법은 문제에 따라 다른데, 실수 값을 예측하는 회귀 문제(예를 들어 지난 포스팅에서 $y=wx+b$ 관계)에서는 평균 제곱 오차(MSE)를 사용하고, 입력이 주어졌을 때 가장 가까운 유형을 찾는 분류 문제(예를 들어 이번 포스팅에서의 의류 판별 문제)에서는 Cross-entropy를 사용한다고 한다. 여기서는 sparse_categorical_crossentropy 가 손실 함수로 사용되었는데, 이는 분류의 결과가 one-hot 인코딩이 아닌 정수로 나타내어졌을 때 사용한다고 한다. 여기서도 10개 아이템의 분류 결과를 0부터 9까지의 정수로 나타내었는데, 만약 one-hot 인코딩을 통해 [1, 0, ..., 0], ..., [0, 0, ..., 1] 처럼 나타났다면 categorical_crossentropy 를 사용하게 될 것이다.

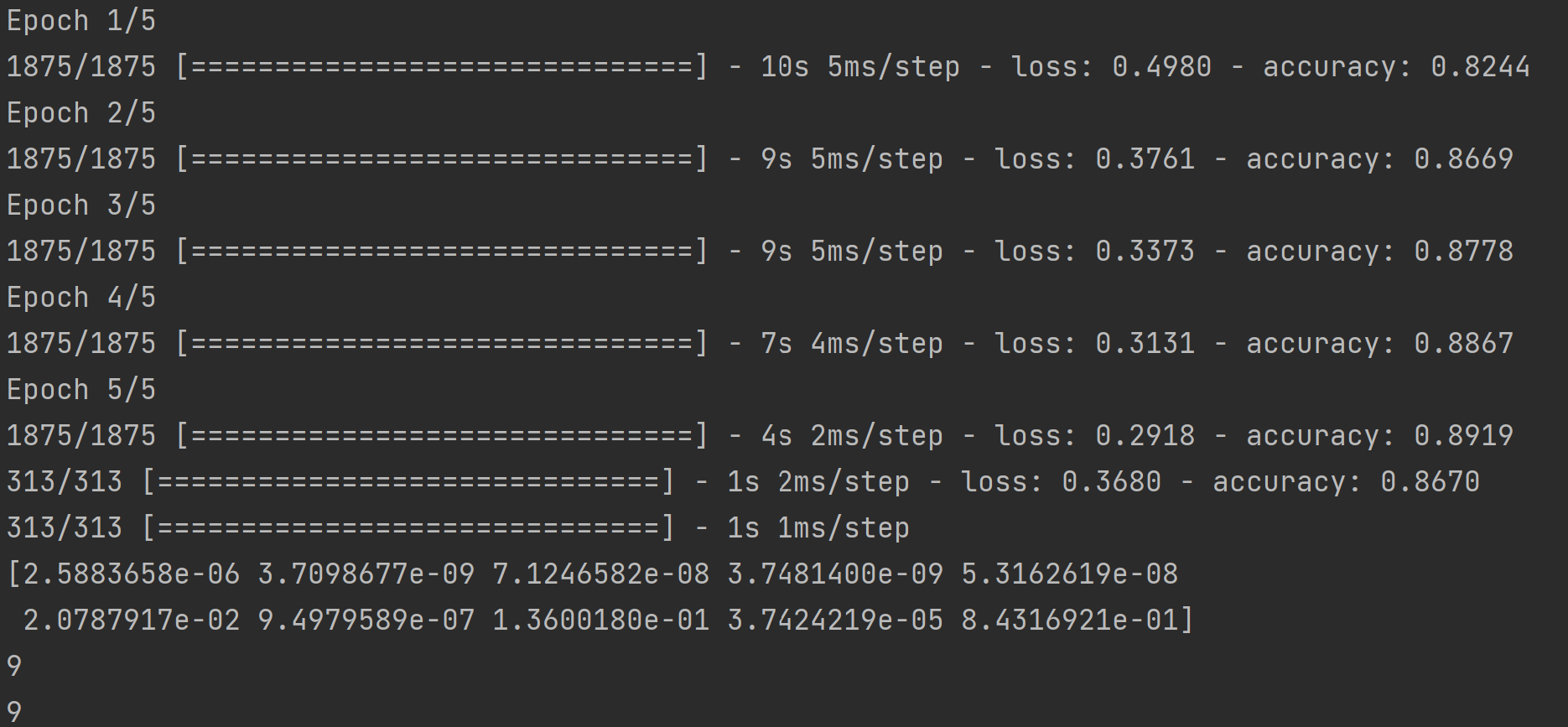
본론으로 돌아와서, 위의 전체 코드를 실행한 결과 5번의 epoch 후 훈련 정확도가 약 89.1%, 테스트 정확도가 약 86.7%로 도출되었다. 또한 훈련된 모델에 테스트 데이터를 입력한 결과, 출력층 10개의 뉴런에서 마지막 값(index = 9)이 가장 큰 값을 갖게 되어 정답과 일치하는 결과를 얻을 수 있었다.

그렇다면, epoch 수를 늘렸을 때 성능이 향상된다고 볼 수 있을까? epoch 수를 50으로 늘렸을 때의 결과는 아래와 같다.

훈련 정확도는 약 96.2%로 월등히 향상되었지만 테스트 정확도는 약 88.4%로 크게 향상되지 않아, 훈련 데이터에서만 잘 동작하는 과대적합이 일어났다고 볼 수 있다. 이를 피할 수 있는 여러 가지 방법은 나중에 설명한다고 한다.

한편, 지금까지는 훈련에 필요한 epoch의 수를 고정하였는데, tf.keras.callbacks.Callback 클래스를 상속받아 사용하면 목표하는 훈련 정확도에 도달하였을 때 훈련을 조기 종료할 수도 있다.

class myCallback(tf.keras.callbacks.Callback):
    def on_epoch_end(self, epoch, logs={}):
        if logs.get('accuracy') > 0.95:
            print("\n훈련 정확도 95% 도달로 인한 종료\n")
            self.model.stop_training = True


callbacks = myCallback()

# 기존의 방식대로 model.compile()까지 완료

# 훈련 시작
model.fit(training_images, training_labels, epochs=50, callbacks=[callbacks])

삽질 후기

지난 삽질도 사실 간단히 해결할 수 있는 문제였긴 하지만, 지난 삽질 덕분인지 이번에는 책에 있는 코드를 그대로 작성했을 때 잘 작동해서 코드 부분에서는 삽질을 할 필요가 없었지만, 이 책 자체가 수학적 개념보다는 Tensorflow와 Keras를 활용하는 데에 초점이 맞추어져 있다 보니 optimizer와 손실 함수를 선정할 때에도 '왜 이걸 쓰지?'와 같은 의문이 들어서 계속 인터넷을 찾아보았다. 사실 현대에 쓰이는 알고리즘들이라 수학적으로 깊이 있게 이해하기는 힘들었지만 그래도 인터넷에 있는 간단한 설명들을 읽어보니 그 이유를 조금이나마 알 수 있었고, 책에서 일단 따라해 보라는 것들이 있더라도 한 번쯤은 의문을 가져보니 도움이 어느 정도 된 것 같다!

또, 이번 패션 MNIST 데이터셋에서 은닉층의 뉴런을 128개로 정한 것에 대해서도 의문이 들었는데 은닉층을 얼마나 만들어야 할지, epoch은 어느 정도로 해야 할지, optimizer와 손실 함수는 어떻게 골라야 할지와 같은 고민들을 앞으로 많이 하게 될 것 같지만 책에서도 특별한 법칙이 있다는 것이 아니라 여러 가지 조건에서 실험해 보아야 한다는 만큼, 앞으로 머신러닝을 통해 내가 원하는 목표를 달성하기 위해서는 많은 경험과 삽질이 필요할 것 같다는 생각이 들었다...!