Paper Review [Mixtral of Experts]

이상민·2024년 1월 23일

논문리뷰

목록 보기

13/29

paper : https://arxiv.org/pdf/2401.04088.pdf

Abstract

Mixtral 8 x 7B : Sparse Mixture of Experts (SMoE) language Model

Mistral 7B와 같은 구조를 가지고 있지만, 각 층이 8개의 Feedforward blocks(i.e. experts)로 구성되어 있는 차이점이 있다. 각 토큰에 대해 각 층에서 router network는 현재 state를 처리하고 그들의 출력을 결합할 두 전문가(experts)를 선택한다. 각 토큰은 오직 두 전문가들만 보지만, 각 timestamp에서 선택된 전문가들은 다를 수 있다. 결과적으로 각 토큰은 47B parameters에 접근할 수 있지만, inference 동안엔 오직 13B 활성 parameters만을 사용한다. Mixtral은 32k 토큰의 context size로 훈련되고, 평가된 모든 벤치마크에서 LLaMA 2 70B와 GPT-3.5를 능가하거나 일치한다. 특히, Mixtral은 수학, 코드 생성, 다국어 벤치마크에서 LLaMA 2 70B를 크게 능가한다.

또한 Instructions을 따르게 fine-tuning된 모델을 제공한다 : “Mixtral 8 x 7B - Instruct”
⇒ 사람 벤치마크에서 GPT-3.5 Turbo, Claude-2.1, Gemini Pro, LLaMA 2 70B - chat modeld을 능가한다.

Base와 instruct 모델은 모두 Apache 2.0 license 하에서 출시된다.

1. Introduction

본 논문에서 가중치가 공개되어있고, Apache 2.0 하에서 라이센스된 Sparse Mixture of Experts model(SMoE)인 Mixtral 8x7B를 제안한다. Mixtral은 대부분의 벤치마크에서 LLaMA 2 70B와 GPT-3.5보다 성능이 좋다. 각 토큰에 대해 그 parameters의 subset만을 이용하기 때문에, Mixtral은 낮은 batch-size에서 빠른 inference 속도를, 큰 batch-size에서 높은 처리량을 가능하게 한다.

Mixtral : Sparse mixture-of-experts network.
⇒ 8개의 별개의 parameters 그룹에서 feedforward block이 뽑힌 decoder-only model

모든 layer에서 모든 토큰에 대해 router network는 토큰을 처리하고 추가적으로 그들의 출력을 합치기 위해 이 그룹들(8개의 별개의 parameters group; “experts”)에서 2개를 뽑는다. 모델이 토큰당 총 parameters의 일부분만을 사용하기 때문에, 이 기술은 비용과 latency를 제어하며 모델의 parameters의 수를 증가시킨다.

Mixtral은 32k 토큰의 context size를 사용해 다국어 데이터로 pretrained 된다. Mixtral은 여러 벤치마크에 대해 LLaMA 2 70B와 GPT-3.5의 성능과 일치하거나 능가한다. 특히, Mixtral은 수학, 코드 생성, 다국어 이해가 필요한 tasks에서 우수한 능력을 보여주며, 이러한 도메인에서 LLaMA 2 70B를 크게 능가했다. 실험들은 Mixtral이 시퀀스 길이와 시퀀스에서 정보의 위치에 관계없이 context window of 32k tokens으로부터 성공적으로 정보를 검색할 수 있음을 보였다.

Mixtral 8x7B - Instruct : Supervised fine-tuning과 Direct Preference Optimization을 사용해 instructions을 따르게 fine-tuning 한 chat model

Mixtral 8x7B - Instruct 성능은 사람 평가 벤치마크에 대해서 GPT-3.5 Turbo, Claude-2.1, Gemini Pro, LLaMA 2 70B - chat model을 크게 능가한다. Mixtral - Instruct는 또한 BBQ, BOLD와 같은 벤치마크에서 편향을 줄이고, 더 균형잡힌 sentiment profile을 보여준다.

Mixtral 8x7B 와 Mixtral 8x7B - Instruct를 Apache 2.0 license 하에서 학술적, 상업적 용도에 무료로 출시하며, 다양한 응용 분야에 대해 광범위한 접근과 잠재력을 보장한다. 커뮤니티가 Mixtral을 완전 오픈 소스 스택과 함께 실행할 수 있도록 효율적인 추론을 위해 Megablocks CUDA 커널을 통합하는 vLLM 프로젝트에 변경 사항을 제출했다. 또한 Skypilot을 통해 클라우드의 모든 인스턴스에 vLLM 엔드포인트를 배포할 수 있다.

2. Architecture

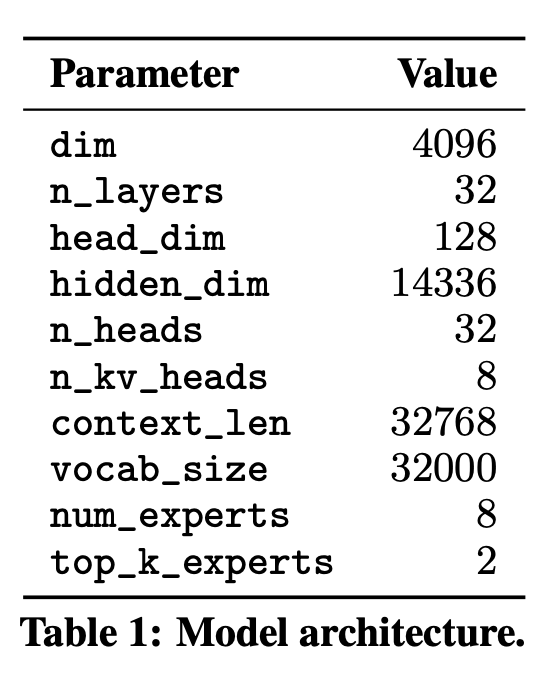
Mixtral은 transformer 구조를 기반으로 하며 Mixtral은 fully dense context length of 32k tokens를 지원한다. Mixtral은 Feedforward blocks가 Mixture-of-Exper layers로 대체된다는 것을 제외하고는 Mistral 7B에서 설명된 것과 동일한 수정을 사용한다. 모델 구조의 parameters는 Table 1에 요약되어있다.

2.1 Sparse Mixture of Experts

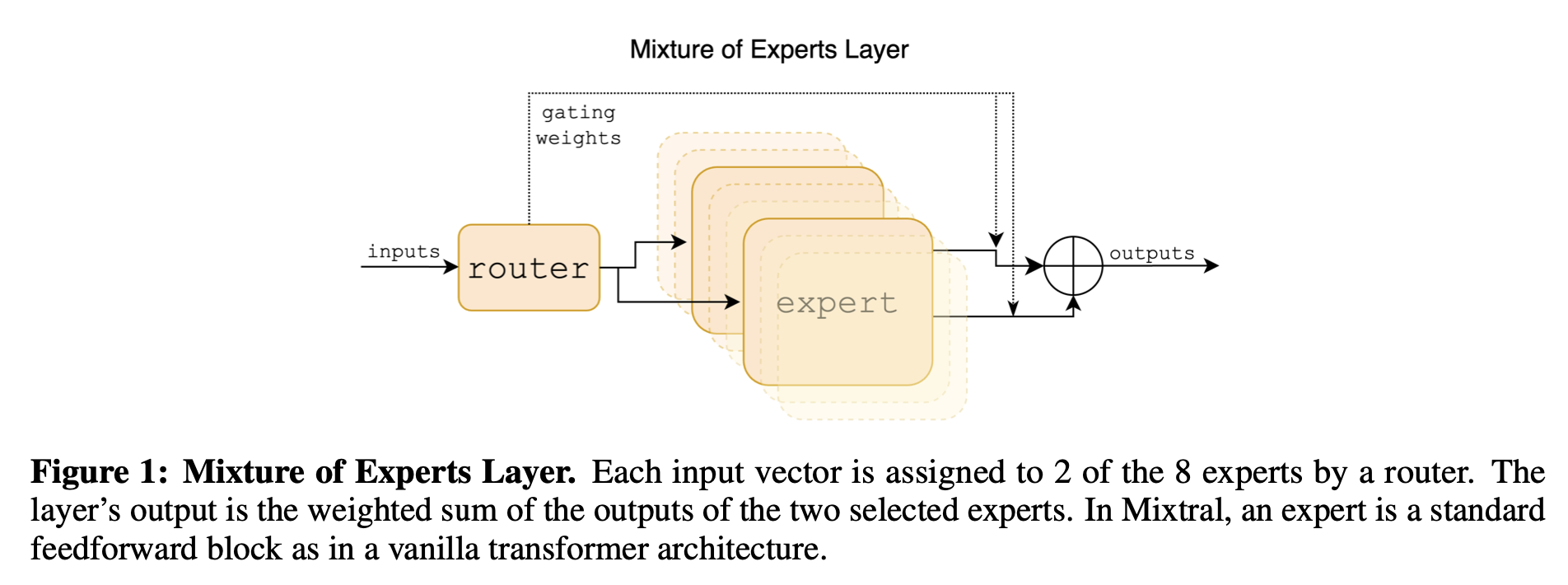
Figure 1에서 Mixture of Experts layer의 간단한 overview를 보여준다. 보다 자세한 overview는 “A review of sparse expert models in deep learning.”를 봐라. 주어진 입력 $x$ 에 대한 MoE 모듈의 출력은 expert networks의 출력의 가중 합으로 결정되며, 여기서 가중치들은 gating networks의 출력에 의해 주어진다. 즉, 주어진 n개의 expert networks { $E_0, E_i, \dots, E_{n-1}$ }에서, expert layer의 출력은 다음과 같다:

\sum_{i=0}^{n-1} G(x)_i \cdot E_i(x)

여기서 $G(x)_i$ 는 $i$ 번째 expert에 대한 gating network의 n 차원의 출력이고, $E_i(x)$ 는 $i$ 번째 expert network의 출력이다. 만약 gating vector가 sparse하면, gates가 0인 experts의 출력 계산을 피할 수 있다. $G(x)$ 를 구현하는 다수의 대안 방법들이 있지만, 간단하고 성능이 좋은 것은 linear layer의 Top-k logits에 대해 softmax를 취하며 구현되는 것이다. 우리는 다음을 이용한다:

G(x) := \text{Softmax(TopK(}x \cdot W_g)),

만약 $l_i$ 가 logits $l \in \R^n$ 의 top-K coordinates 중에 있다면, top-K $\text{TopK}(l)_i := l_i$ 이고 그렇지 않다면 $(\text{TopK}(l))_i := -\infty$ . 토큰당 사용되는 experts의 수인 K의 값은 각 토큰을 처리하는데 사용되는 계산량을 조절하는 hyper-parameter이다. 만약 K를 고정시킨 상태에서 n을 증가시키면, 계산 비용을 효과적으로 일정하게 유지하면서 모델의 파라미터 수를 증가시킬 수 있다. 이는 n과 함께 증가하는 “모델의 총 parameter 수”(흔히 sparse parameter count로 불리는)와 K와 함께 n까지 증가하는 “개별적 토큰을 처리하는데 사용되는 parameters의 수”(active parameter count)를 구별하는 동기를 부여한다.

MoE layers는 고성능 전문 커널이 있는 단일 GPU에서 효율적으로 실행될 수 있다. 예를 들어, Megablocks는 MoE layers의 FFN operations을 큰 sparse matrix multiplication으로써 cast하여, 실행 속도를 크게 향상시키고 서로 다른 전문가들이 할당받는 토큰의 개수가 가변적인 경우를 자연스럽게 처리한다. 게다가, MoE layer는 기본 모델 병렬화 기술과 Expert Parallelism(EP)라고 불리는 특정 파티셔닝 전략을 통해 다수의 GPU에 분배될 수 있다. MoE layer의 실행 동안 특정 전문가에 의해 처리되어야 하는 토큰은 처리를 위해 해당 GPU로 routed되고, 전문가의 출력은 원래의 토큰 위치로 반환된다. EP는 개별 GPU의 과부화와 계산 병목 현상을 방지하기 위해서 GPU들에 걸쳐 workload를 고르게 분산하는 것이 필수적이기 때문에, EP는 load balancing에 과제(challenges)를 도입한다.

Transformer 모델에서 MoE layer는 토큰마다 독립적으로 적용되며 transformer block의 FFN sub-block을 대체한다. Mixtral의 경우, 전문가 함수 $E_i(x)$ 와 동일한 SwiGLU 구조를 사용하고 K=2로 설정한다. 이는 각 토큰이 가중치가 다른 SwiGLU sub-blocks 2개로 routed되는 것을 의미한다. 이를 모두 종합하면, 입력 토큰 $x$ 에 대한 출력 $y$ 는 다음과 같이 계산된다:

y = \sum_{i=0}^{n-1} \text{Softmax(Top2}(x \cdot W_g))_i \cdot \text{SwiGLU}_i(x)

GShard는 모든 다른 블록을 대체하는 반면 우리는 FFN sub-blocks를 MoE layer로 대체하고, GShard는 각 토큰에 할당된 두 번째 전문가를 위해 더 정교한 gating 전략을 사용하는 것을 제외하면, 이 공식은 GShard 구조와 유사하다.

내가 이해한 바

Gate 부분과 Expert 부분으로 나뉜다.
Expert는 그룹의 수만큼 있다. $\to$ 여기선 8이겠지? (8개 중에 2개를 뽑는다 했으니)
그래서 $\text{SwiGLU}_i(x)$ 이다. ( $i$ 번째 SwiGLU를 이용하니)
그리고 Gate 부분은 $W_g$ 에 의해 계산된 vector가 생길 것이고, 여기선 8차원일 것이다 ( $\because$ 8개의 Experts에 대해 가중치를 줘야하니까 )
TopK가 아니면 $-\infty$ 를 반환한다. 왜냐하면 Softmax의 특성 때문인데, $e^{-\infty} \approx 0$ 이 되어 sparse matrix multiplication을 할 수 있게 되기 때문이다.

즉, $\text{Softmax(Top2}(x \cdot W_g))_i$ 으로 Experts들에게 가해질 가중치를 계산해주고(2개는 값이, 나머지는 0이 나올 것이다), $\text{SwiGLU}_i(x)$ 로 Experts들의 값을 계산해준다.
최종적으로 나온 것들이 2개 Experts의 weighted sum이 될 것이다.
$\Rightarrow$ 2개의 Experts parameters만 Active 상태가 된다.

5. Routing Analysis

이 섹션에서 router에 의한 전문가 선택에 대한 작은 분석을 수행한다. 특히 훈련 기간 동안 몇몇 전문가들이 특정 도메인(e.g. 수학, 생물학, 철학 등)에 특화되는지를 확인하는데 흥미가 있다.

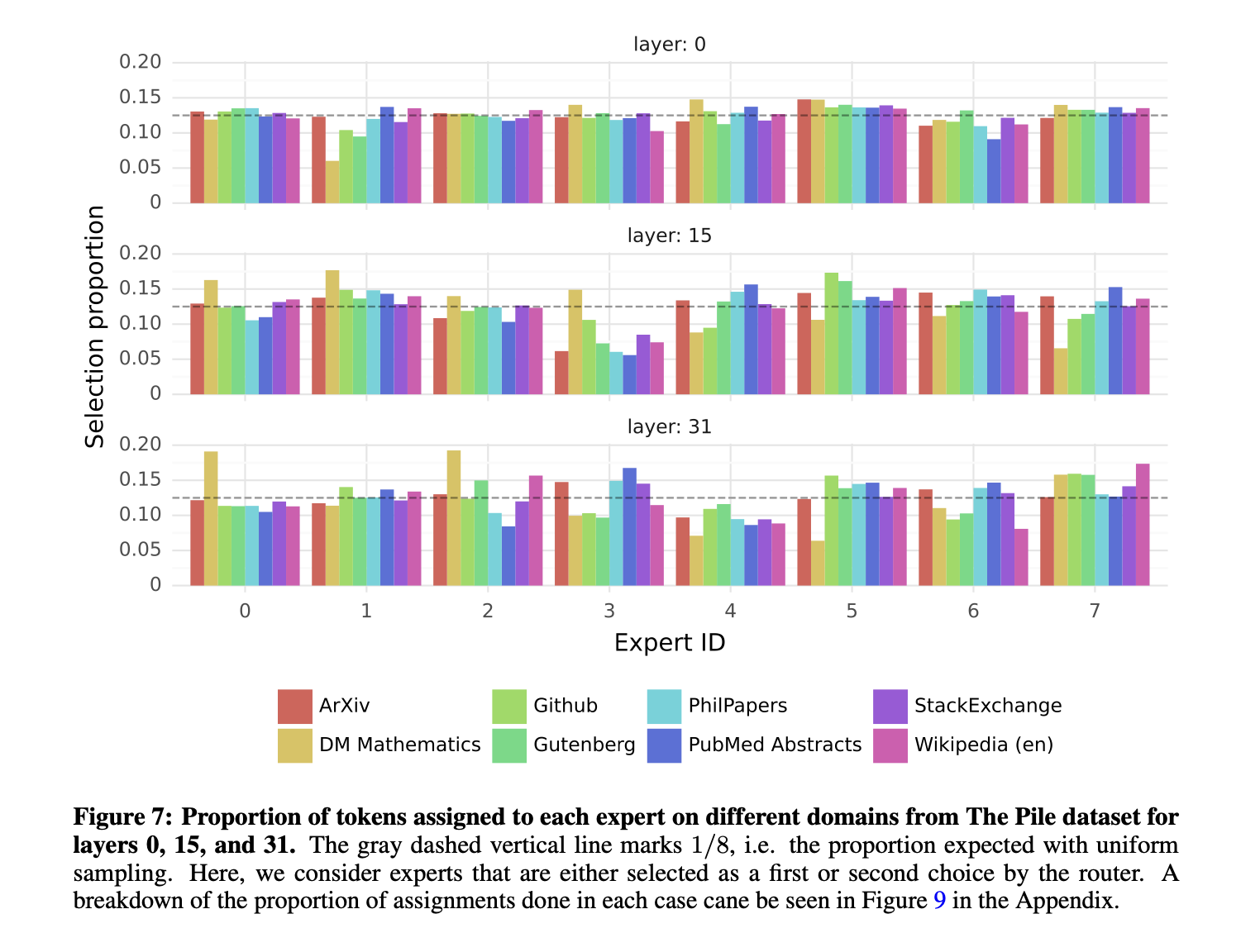
이를 조사하기 위해서, The Pile validation dataset의 서로 다른 subsets에 대한 선택된 전문가의 분포를 측정한다. Layer 0, 15, 31에 대한 결과는 Figure 7에 있다(layer 0과 layer 31은 각각 모델의 첫 번째 층과 마지막 층이다). 놀랍게도 토픽에 기반한 전문가들(experts) 할당의 명백한 패턴을 발견하지 못했다. 예를 들어, 모든 층에서 ArXiv papers(Latex로 적혀진), biology(PubMed Abstracts), Philosophy(PhilPapers) 문서에 대한 전문가 할당 분포는 매우 유사하다.

우리는 오직 DM Mathematics에 대해서만 약간 다른 전문가의 분포를 보았다. 이러한 차이는 데이터셋의 통합적인 특성과 자연어 스펙트럼의 제한된 적용 범위의 결과일 가능성이 높으며, 특히 hidden state가 입력/출력 임베딩과 각각 매우 연관되어있는 first, last 층에서 두드러진다.

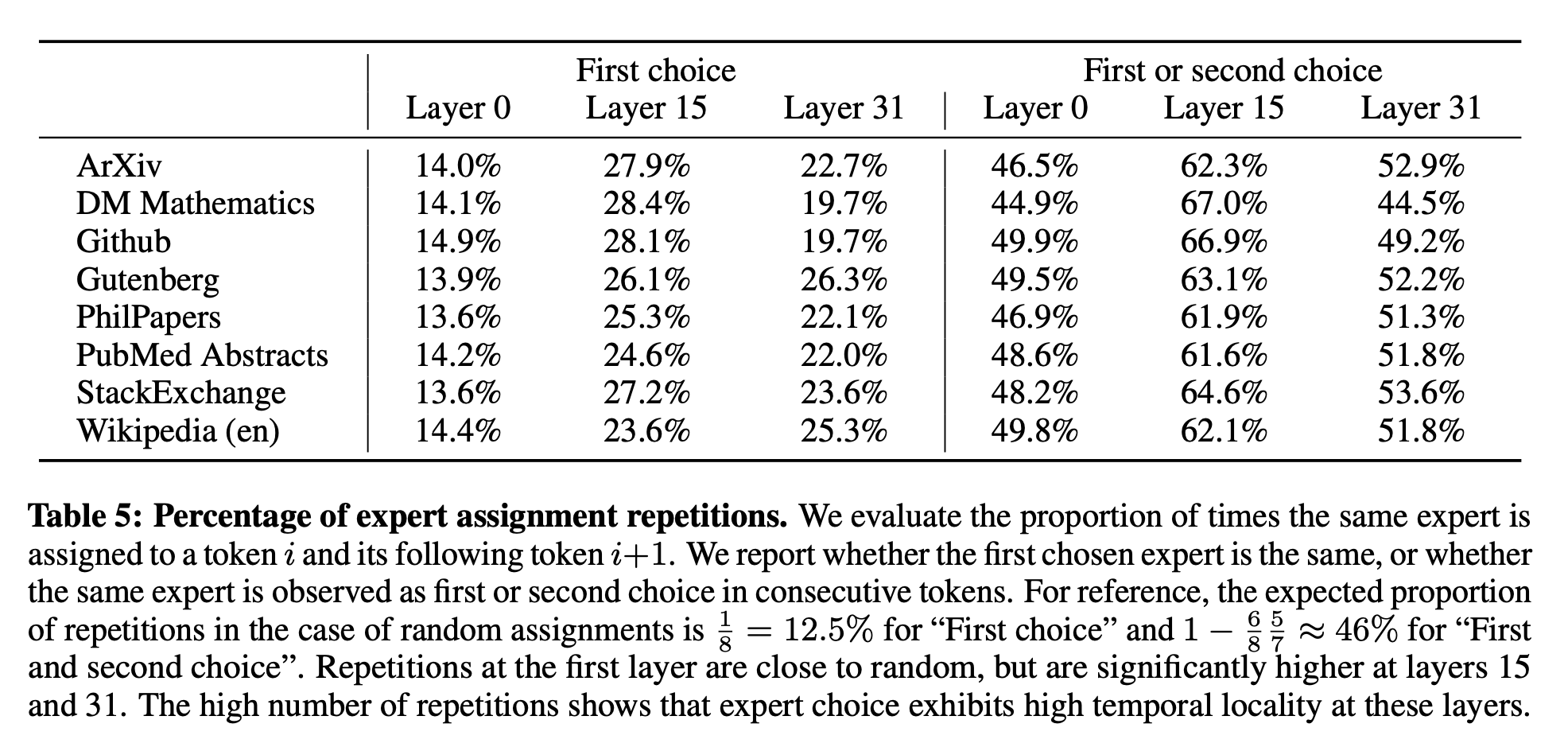
Figure 8로부터 연속적인 토큰들이 같은 전문가들에 종종 할당되는 것을 주목했다. 사실 The Pile 데이터셋에서 약간의 positional locality를 발견한다. Table 5는 도메인과 층 당 같은 전문가 할당을 갖는 연속적인 토큰들의 비율을 보여준다. 높은 층에서 반복된 연속 할당의 비율은 랜덤보다 상당히 높다. 이는 빠른 교육과 추론을 위해 모델을 최적화하는 방법에 영향을 미친다. 예를 들어, 높은 locality를 갖는 경우는 전문가 병렬화를 할 때 특정 전문가들의 over-subscription을 유발할 가능성이 높다. 반대로 locality는 “Fast inference of mixture-of-experts language models with offloading”논문에서와 같이 캐싱에 활용될 수 있다. 모든 층과 데이터셋에 전반에 걸친 이러한 동일한 전문가 빈도에 대한 보다 완벽한 보기는 Appendix의 Figure 10에서 볼 수 있다.

6. Conclusion

본 논문에서 open-source 모델들 중 SOTA 성능을 달성한 첫 mixture-of-experts network인 Mixtral 8x7B를 소개했다. Mixtral 8x7B Instruct는 사람 평가 벤치마크에 대해 Claude-2.1, Gemini Pro, GPT-3.5 Turbo를 능가한다. 각 time step에서 오직 2개의 전문가들만 사용하기 때문에, Mixtral은 토큰당 오직 13B active parameters를 이용하여 토큰당 70B parameters를 사용한 이전 최고의 모델(LLaMA 2 70B)을 능가한다. 우리는 우리의 모델을 Apache 2.0 license 하에서 공적으로 이용가능하게 만들었다. 우리의 모델을 공유함으로써 다양한 산업과 도메인에 이점을 줄 수 있는 새로운 기술들과 어플리케이션들 발전을 촉진하는 것을 목표로 한다.

느낀점

특정 domain에 대한 정보를 특정 experts가 학습을 한다면 각 도메인에 대한 fine-tuning 과정이 필요없어지지 않을까 싶었다.(각 domain에 따라 활성화되어 학습되는 parameters가 다를 것이니 fine-tuning의 수고가 좀 덜지 않을까?). 그리고 특정 experts만 학습하면 되기에 활성화되는 parameters의 수도 줄어들 것이라 좋아 보였다. 하지만 결과에서 볼 수 있듯이 특정 domain에 특정 experts가 사용되지는 않는다. 그럴 수 있는게, 어떤 문장을 받았을 때 토큰 별로 experts가 지정이 되니까 token 별로 domain의 특성을 띄어야하는데 그러기가 힘들 것으로 보았다. 단어가 특정 domain의 특성을 무조건적으로 띄진 않기 때문이다. 즉, 한 단어가 여러 domain에서 쓰일 수 있고, "나는" 같은 단어는 도메인에 관련없는 단어이기 때문이다.

문장에서 특정 도메인의 성격을 띌 수 있는 단어가 얼마나 있을까? 있어도 많지 않을 것 같다. 그렇기에 특정 Experts의 비율이 크지 않고, 분포가 비교적 일정했던 것 같다.

생각과 시도는 좋았지만, 아쉬운 결과인 것 같다.