우선적으로 직역을 바탕으로 논문을 리뷰하는 것을 밝힙니다.
Paper : https://arxiv.org/abs/2012.07436
Abstract
현실의 applications은 전력 소비 계획과 같은 시계열의 긴 series 예측을 요구한다. LTSF는 input과 output의 정확한 장거리 의존성 결합을 효율적으로 포착하는 높은 예측 능력을 요구한다. 최근 연구는 예측 능력을 향상시킬 수 있는 transformer의 잠재력을 보여주고 있다. 그러나 transformer에는 2차 시간 복잡도, 높은 메모리 사용량, encoder-decoder 구조의 고유의 한계를 포함해 transformer를 LTSF 문제에 직접 적용할 수 없는 몇 가지 심각한 문제들이 있다. 이러한 문제를 해결하기 위해 Informer라는 이름의 LSTF를 위한 효율적인 transformer 기반 모델을 설계한다:
(1) ProbSparse self-attention 메커니즘 : 문장 의존성 정렬(sequences’ dependency alignment)에서 비슷한 성능을 내면서 시간 복잡도와 메모리 사용량에서 를 달성
(2) Self-attention distilling : 계단식 레이어 입력을 절반으로 줄임으로써 dominating attention를 강조하며, 극단적으로 긴 입력 시퀀스를 효율적으로 다룹니다
(3) Generative style decoder : 개념적으로는 간단한데, 긴 시계열 예측을 step-by-step으로 하지 않고 한 번의 forward operation으로 함으로써 긴 시계열 예측의 추론 속도를 크게 향상 시킴.
4개의 대규모의 데이터셋에 대한 광범위한 실험은 기존의 방법들을 크게 능가하고, LSTF 문제에 새로운 solutions을 제공한다.
Introduction
시계열 예측은 많은 도메인에서 중요한 요소이다. 여러 도메인의 여러 문제에서 장기 시계열 예측(Long Sequence Timeseries Forecasting: LSTF)라고 불리는 과거의 행동에 대한 많은 시계열 데이터를 활용하여 장기적인 예측을 수행할 수 있다. 그러나 기존의 모델들은 대부분 short-term problem setting(보통 48개의 점 또는 그 이하의 예측)에 맞춰 설계되었다. 점점 길어지는 sequence는 모델의 예측 능력에 부담을 주고, 이러한 추세는 LTSF에 대한 연구를 이어나가고 있다.
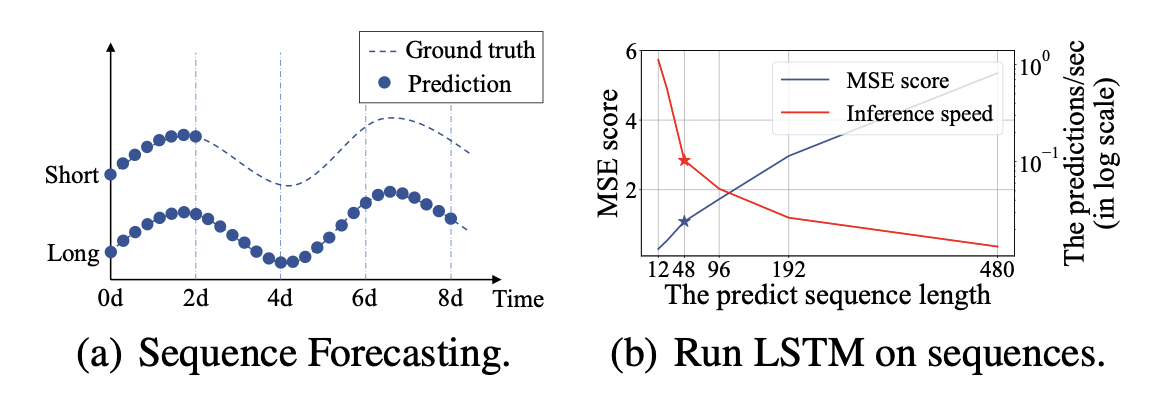
경험적인 예시로 위를 봐보자.
이는 LSTM으로 변전소(electrical transformer station)의 온도를 매 시간 예측한 것이다.
short-term period : 12 points, 0.5 days
long-term period : 480 points, 20 days
전체적인 성능 차이는 sequence length가 48보다 클 때 상당해진다. (위의 그림 (b)를 보면) MSE는 만족스럽지 못한 성능으로 상승하며 추론 속도가 급격히 감소한다. 그리고 LSTM 모델은 실패하기 시작한다.
장기 시계열 예측(LSTF)에 대한 주요 과제는 점점 더 긴 sequnce의 수요를 충족하기 위해 예측 능력을 향상시키는 것이다. 이는 다음과 같은 것들을 필요로 한다.
- (a) Extraordinary long-range align 능력
- (b) 긴 sequence 입력과 출력에 대한 효율적인 연산
최근에 transformer 모델은 RNN 모델보다 긴 범위의 의존성(long-range dependency)을 잡는 것에 우수한 성능을 보여주었다. Self-attention 메커니즘은 네트워크에서 신호 이동 경로의 최대 길이를 이론적인 최단 경로인 O(1)로 줄일 수 있고 반복 구조를 피할 수 있다. 이로 인해 transformer는 LSTF 문제에 큰 잠재력이 있음을 보여주었다. 그럼에도 불구하고, self-attention 메커니즘은 L-길이의 입력/출력에 대한 L-2차 연산과 메모리 소비 때문에 요건 (b) (위의 긴 sequence 입력과 출력에 대한 효율적인 연산)을 위반한다. 일부 대규모 transformer 모델은 리소스들을 투입하고 NLP task에 인상적인 결과를 낳았다(Brown et al. 2020). 그러나 학습 과정에서 수십 개의 GPU를 이용하고 비싼 배치 비용은 이러한 모델들이 실제 LSTF 문제에 비싸서 이용할 수 없게 만든다. Self-attention 메커니즘과 transformer 구조의 효율성이 self-attention과 transformer구조를 LTSF 문제에 적용하는 과정에서 병목 현상이 된다. 그래서, 이 논문에서 우리는 다음 물음에 대한 답을 찾고자 한다 :
Transformer 모델을 더 높은 예측 능력 유지 뿐만 아니라 연산, 메모리, 구조 효율성을 향상 시킬 수 있을까?
기본 transformer는 LSTF 문제를 푸는데 3가지 중요한 한계를 가지고 있다.
-
The quadratic computation of self-attention(self-attention의 2차 연산)
: Canonical dot-product라고 불리는 self-attention 메커니즘의 atom operation(모델의 기본적인 연산 혹은 더 이상 분해되지 않는 가장 작은 연산)은 레이어당 의 시간 복잡도와 메모리 사용량을 유발한다.
-
The memory bottleneck in stacking layers for long inputs(긴 input을 위해 층을 쌓을 때 발생하는 메모리 병목 현상)
: J개의 encoder/decoder 층을 쌓는 것은 메모리 사용을 총 로 만든다. 이는 긴 sequence input을 받을 때 모델의 확장성을 제한한다.
-
The speed plunge in predicting long outputs(긴 outputs을 예측할 때의 속도 급락)
: 기본 transformer의 dynamic decoding은 RNN 기반의 모델과 같이 느린 step-by-step 추론을 한다.
Self-attention의 효율성을 향상시키기 위한 몇 가지 선행 연구들이 있다. 모두 한계 1번을 다루기 위해 효율성 향상이 제한되어 있는 heuristic 방법을 이용하고 self-attention 메커니즘의 복잡도를 로 줄여준다(The Sparse Transformer 2019, LogSparse Transformer 2019, Longformer 2020). Reformer 는 locally - sensitive hashing attention을 이용해서 을 달성했는데 이는 오직 매우 긴 sequence에서만 작동한다. 최근에는 Linformer는 선형 복잡도 을 주장했는데, 그러나 실제 세계의 긴 sequence input에 대해 project matrix를 고정할 수 없어서 로의 저하 위험이 있다. Transformer-XL과 Compressive Transformer는 긴 범위의 의존성을 잡기 위해 보조의 hidden state를 이용한다. 이는 한계 1번을 증폭시키고, efficiency bottleneck을 깨는 것에 악영향을 줄 수 있다. 이러한 모든 작업들은 주로 1번 한계에 초점이 맞춰져있고 LTSF 문제에 대해 2,3번 한계들은 풀리지 못한 상태로 남아있다. 예측 능력을 향상시키기 위해서는 모든 한계들을 다뤄야하고, 제안하는 informer에서 효율성 이상의 개선을 달성한다.
이를 위해, 우리의 작업은 명백히 3가지 문제를 탐구한다. self-attention 메커니즘에서 sparsity(희소성)를 조사하고, network components의 향상을 만들고, 광범위한 실험을 설계한다. 본 논문의 기여는 다음과 같이 요약된다 :
- LSTF 문제에서 성공적으로 예측 능력을 향상시키기 위해 장기 시계열 출력과 입력간의 개별적 장거리 종속성(individual long-range dependency)를 잡아내며 transformer와 유사한 모델의 잠재적 가치를 입증하는 Informer를 제안한다.
- Canonical self-attention을 효과적으로 대체하는 ProbSparse self-attention 메커니즘을 제안한다.
- J-stacking layer에서 dominating attentioin scores를 부여하고, 시간 복잡도를 로 대폭 줄여 긴 sequence input을 받게 도와주는 self-attention distilling operation을 제안한다.
- 긴 sequence output을 하나의 forward step만에 얻어 inference 단계동안 누적 오류 확산을 피하는 generative style decoder를 제안한다.
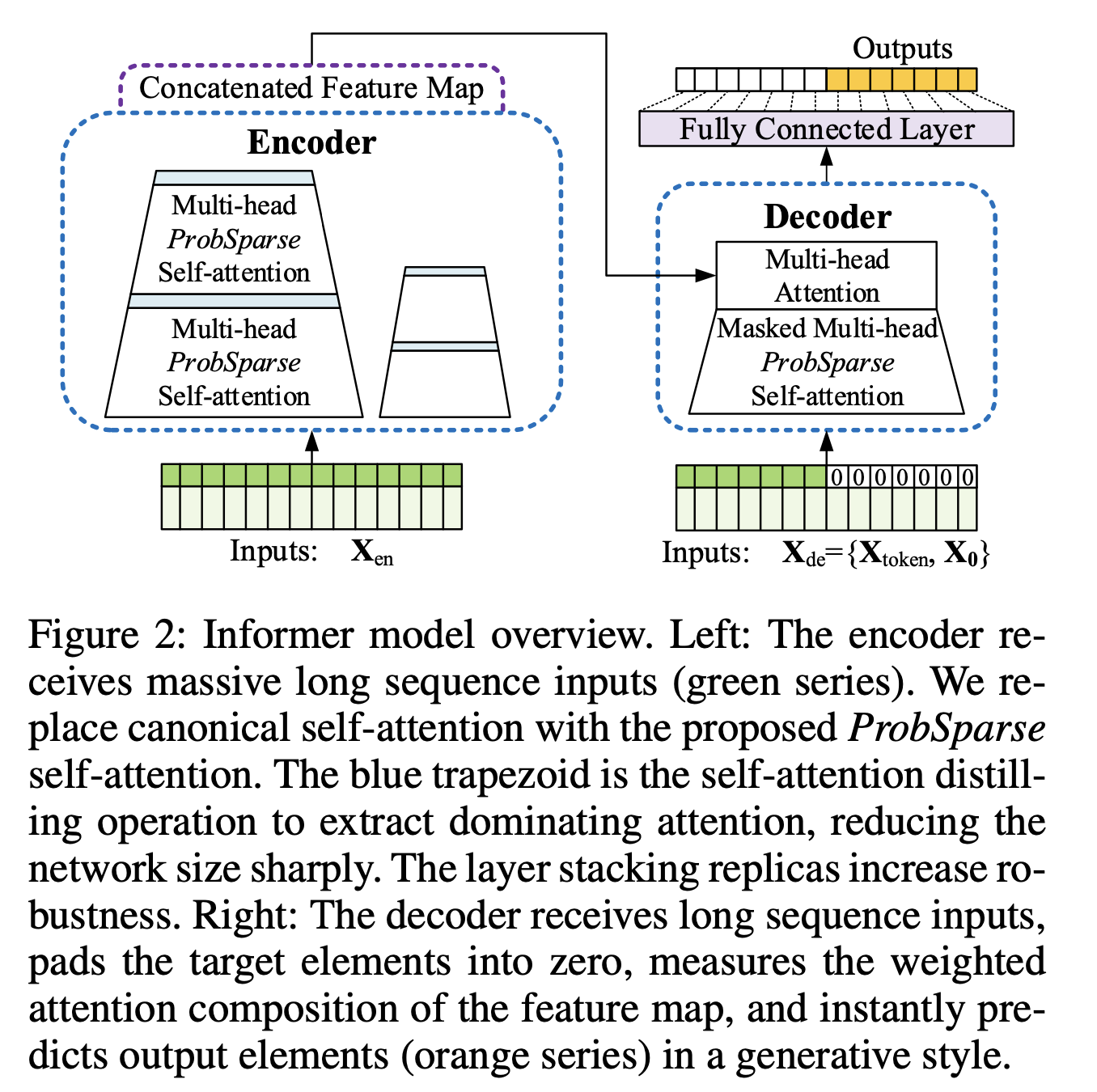
그림 설명(Figure 2)
<왼쪽> : canonical self-attention을 ProbSparse self-attention으로 바꿔주었고, 파란색 점선으로 둘러쌓인 것은 network size를 급격히 줄여주면서 dominating attention을 추출하기 위해 self-attention distilling operation을 하는 것이다. Replicas를 쌓은 layer는 견고함을 증가시킨다.
<오른쪽> : Decoder는 긴 sequence input을 받고, target 요소를 0으로 padding 처리하고, feature map의 weighted attention composition을 측정하고, 즉시 주황색 부분의 series인 output 용소들을 generative style로 예측한다.
Preliminary
고정된 크기의 window가 있는 rolling forecasting setting 하에서, time t에서 input 을 가지고 output은 해당 sequence를 예측하는 것이다. LSTF 문제는 전보다 더 긴 output의 길이를 장려하고 feature dimension은 단변수의 경우로 국한되지 않는다. 즉,
Encoder-decoder architecture : 많은 유명한 모델들은 input representations를 hidden state representations로 ‘encode’ 하고, hidden state representation으로부터 output representations를 ‘decode’하게 고안되었다. Inference는 ‘dynamic decoding’이라고 불리는 step-by-step process를 포함한다. 이는 decoder는 이전 state 로부터 새로운 hidden state 를 계산하고 다음 k-th step으로부터의 다른 필요한 outputs들이 (k+1)-th sequence 를 예측하는 process.
Input Representation : 균일한 입력 표현은 시계열 inputs의 global positional context와 local temporal context를 향상시키기 위해 주어진다.
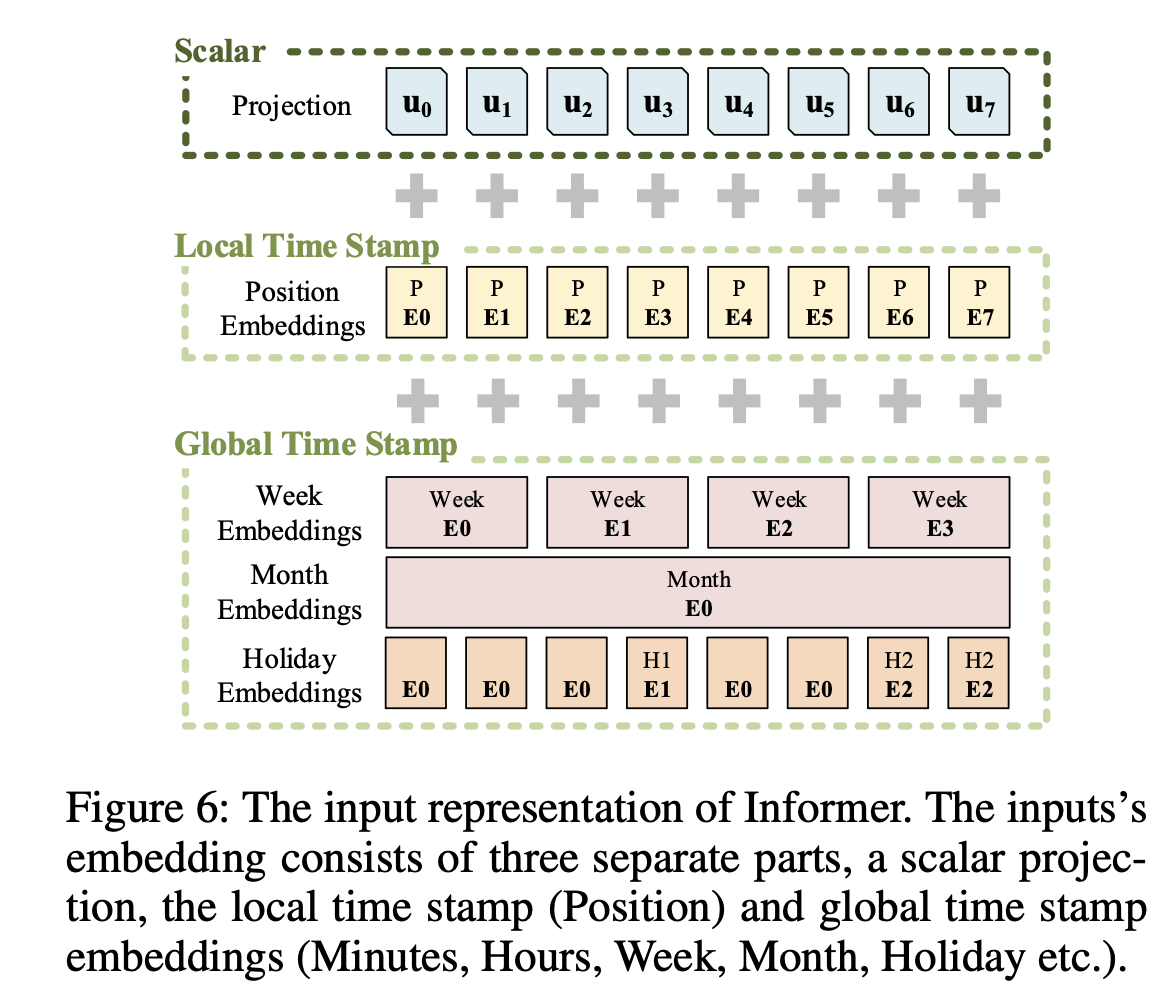
Methodology
기존의 시계열 예측 방법은 크게 2개로 분류할 수 있다. Classic 시계열 모델은 시계열 예측을 위한 신뢰할 수 있는 주역 역할(workhorse)을 하고, deep learning 기술이 주로 RNN과 그 변형들을 이용하여 encoder-decoder 예측 paradigm을 발전시켰다. 우리가 제안한 Informer는 LSTF 문제를 대상으로 하면서 encoder-decoder 구조를 이용한다. Overview는 그림2(figure 2)를 참조하고, 자세한 내용은 아래 절을 참조하길 바란다.
Efficient Self-attention Mechanism
Vaswani et al.2017 논문에서의 canonical self-attention은 tuple inputs에 기반하여 정의되었다. 즉, query, key, value의 scaled dot-product:
그리고 는 input dimension 이다.
Self-attention 메커니즘을 더 자세히 논의하기 위해, 가 Q, K, V의 i번째 row(행)를 나타내도록 한다. Tsai et al. 2019의 공식을 따라, i번째 query의 attention은 확률 형태의 kernel smoother로 정의된다:
where and selects the asymmetric exponential kernel .
Self-attention은 values들을 합치고, 확률 계산을 기반으로 한 outputs을 얻는다. 이는 2차 시간 dot-product 계산이 필요하고, 메모리 사용량이 필요하다. 이러한 메모리 사용량이 필요한 것은 예측 능력을 향상시키는 것에 주된 결점이다.
몇몇 이전 시도는 self-attention의 확률 분포가 potential sparsity를 가지고 있는 것을 드러냈고, 그들은 성능에 큰 영향을 미치지 않고( ’성능이 줄어들지 않고’로 생각하면 될 듯 ) 모든 에 대해 “selective” counting 전략을 설계했다.
- Parse Transformer는 분리된 공간 상관 관계(separated spatial correlation)로부터 희소성이 발생하는 row outputs과 column inputs를 통합한다.
- LongSparse transformer는 self-attention에서 주기적인 패턴을 관찰하고, 각 셀을 지수적인 step size로 이전 셀에 집중하도록 한다.
- Longformer는 이전의 두 작업을 더 복잡한 희소 구성(sparse configuration)으로 확장한다.
그러나 이들은 다음과 같은 heuristic 방법(query와 key를 선택할 때, query와 key의 실질적 의미를 생각하는 것이 아니라 단순히 random하게 또는 일정 window 구간으로 한정하는 방식 등)의 이론적 분석에 제한되어 있으며, 동일한 전략으로 multi-head self-attention을 다루기에 추가 개선이 좁아진다.
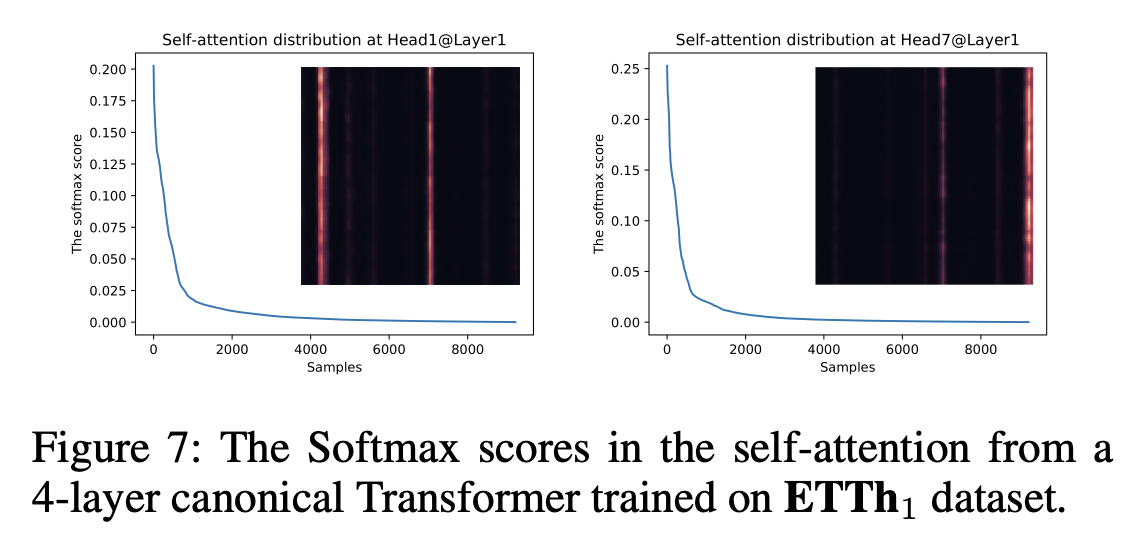
우리의 접근 방식에 동기 부여를 하기 위해, 먼저 canonical self-attention의 학습된 attention 패턴들에 대한 질적 평가를 수행한다. ‘sparsity’ self-attention scores는 긴 꼬리 형태의 분포를 형성한다(long tail distribution). 즉, 적은 dot-product 쌍이 주요 attention에 기여하고 다른 쌍들은 사소한 attention을 만든다. 그렇다면 다음 질문은 ‘어떻게 그들을 구분하는 것인가?’ 이다.
Query Sparsity Measurement
(1)번 equation을 보면, 모든 keys에 대한 i번째 query의 attention은 로 정의되어있고, output은 values 와의 composition이다. Dominant dot-product 쌍들은 해당하는 query’s attention 확률 분포를 균일 분포(uniform distribution)와 달라지게 유도한다 (유의미한 query(i) - keys(all j) pairs 분포는 uniform 분포로부터 상이함). 만약 가 uniform distribution 에 가깝다면, self-attention은 values 의 trivial sum(단순 합)이 되고 residential input에 중복된다(의 중복이라고 보면 될 듯?). 자연적으로, p 분포와 q 분포의 ‘유사성(likeness)’는 중요한 queries를 구별하는 것에 이용될 수 있다. 본 논문에서는 유사성(likeness)을 Kullback-Leibler divergence를 통해 측정했다.
상수를 떨어뜨리면서, i번째 쿼리의 희소성 측정은 아래와 같이 정의한다.
첫 번째 부분은 모든 keys에 대한 q의 Long-Sum-Exp(LSE)이고, 두 번째 부분은 모든 key에 대한 arithmetic mean(산술 평균, 그냥 평균)이다. 만약 i번째 쿼리가 더 큰 를 갖게되면, attention 확률 는 더 “다양(diverse)”해지고, long tail self-attention 분포의 header field에서 dominate dot-product(유의미한 dot-product) 쌍을 가지고 있을 확률이 높다.
ProbSparse Self-attention
제안된 측정에 기반한 ProbSparse Self-attention은 각각의 키가 오직 u개의 dominant queries에만 주의를 기우리도록 허용함으로써 얻어진다 :
여기서 는 같은 크기의 q로 구성된 sparse matrix고, 희소성 측정 값 기준 Top - u개의 queries만을 포함하고 있다. 논문에서는 Sampling factor 상수 에 의해 조정되는 (top 개를 뽑을 때, ) 을 설정한다. 이는 ProbSparse self-attention이 각 query-key lookup마다 dot-product만 계산하면 되게 만들고, layer memory 사용량은 로 유지하게 만든다.
(나의 예상 : each lookup당 )가 드는 것을 보아 key를 개만큼 뽑아서 dominant Queries를 뽑고, Dominant queries(개)와 all keys와 계산하여 attention score를 뽑아야하니까, layer memory 사용량은 이다.)
Multi-head 관점에서, ProbSparse self-attention은 각 head에서 다른 sparse query-key 쌍을 생성하기에 return에서 심각한 정보 손실을 피할 수 있다.
하지만, 를 계산하기 위해 모든 쿼리를 traversing 하는 것은 각 dot-product 쌍의 계산을 요구한다. 즉, 라는 quadratic 시간 복잡도가 발생한다. 게다가 LSE operation은 잠재적인 수치 안정성 문제를 가지고 있다. 이에 동기를 받아, query sparsity measurement의 효율적인 획득을 위한 empirical approximation을 제안한다.
Lemma 1)
For each query and in the keys set , we have the bounds as . When it also holds.
Lemma 1으로부터 아래와 같은 max-mean measurement을 제안할 수 있다:
Top-의 범위는 proposition 1의 boundary relaxation에서 대략적으로 유지된다.
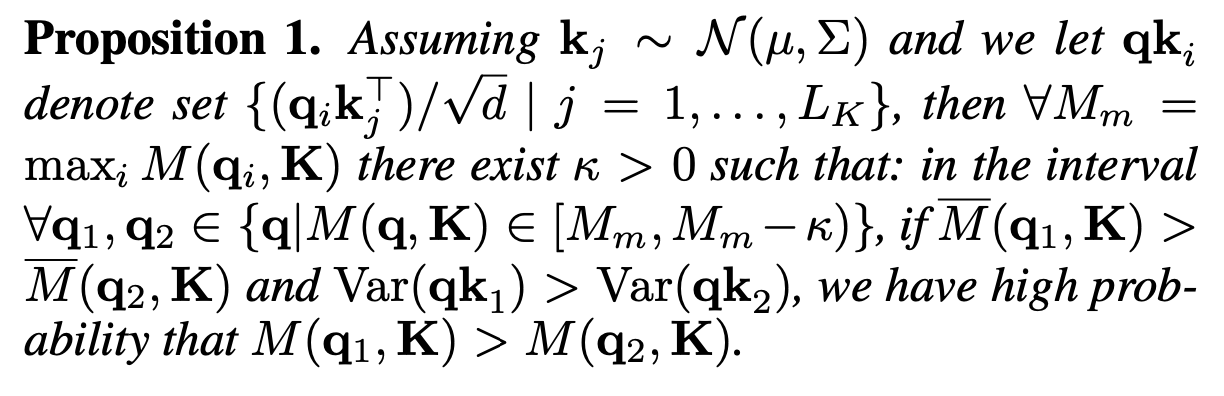
이고 이면, 일 확률이 높다. 즉, 으로 을 알 수 있다!
그렇기에 계산을 줄이기 위해 Long tail 분포 하에서, 를 계산하기 위해 오직 개의 random한 dot-product 쌍의 sample이 필요하다. 즉, 다른 쌍들은 0으로 채운다.
그리고 로써 모든 query와 sampling 된 keys를 통해 계산된 에서 Top-를 뽑는다. 에서 max-operator는 0 값에 덜 민감하고, 수치적으로 안정적이다. 연습에서는, self-attention 계산에서 queries와 keys에서 input 길이는 전형적으로 같다. 즉, 이고, 이로써 ProbSparse self-attention의 시간 복잡도와 공간 복잡도는 이 된다.
<ProbSparse self-attention에 대한 나만의 요약>
Self-attention을 보았을 때, 주요한 keys와 queries의 쌍이 있음을 확인했다. 즉, 주요한 쌍들이 아니면 attention에 주는 효과가 미미했다.
주요한 Top u개의 queries를 이용해 를 만들어서 attention score를 구하자!
그래서 주요한 쌍들을 찾고 싶은데 어떻게 찾나? Kullback-Leibler divergence을 이용해 주요한 쌍들을 찾는데, 우리는 Kullback-Leibler에서 상수항 부분을 뺀 을 이용한다!
그러면 모든 queries와 keys를 다 계산해본다면, 의 quadratic 시간복잡도가 발생한다.
근데 proposition 1을 통해 boundary relaxation이 가능하여 개의 dot-product pairs를 이용하여 를 구할 수 있다.
( 범위 완화를 통해 모든 들을 다 계산하지 않아도 되나보다. (내 생각이며, 이 부분은 이해가 잘 안된다. Proposition 1의 이해 부족인 것 같다.) )
이렇게 구한 의 상위 개를 뽑아 로 만든다.
실제로는 이기 때문에, 총 ProbSparse self-attention의 시간 복잡도와 공간 복잡도는 이 된다.
코드로 보니까,
모든 query와 random하게 sampling된(torch.randint를 이용) key들을 계산하여 dominant u개의 queries 뽑는다.
u = c * 개의 sampling된 keys들과 모든 query를 계산하여 dominant u개의 queries를 뽑는다. Dominant를 계산하기 위해서는 을 이용하는데, 위와 같이 "max 값 - 산술 평균"이다.
Encoder: Allowing for Processing Longer Sequential Inputs under the Memory Usage Limitation
Encoder는 긴 sequential inputs의 강한 장거리 의존성을 추출하도록 설계되었다. Input representation 후에, sequence input의 t번째 은 matrix로 바뀌었다. 명확성을 위해 밑의 fig(3)을 주겠다.
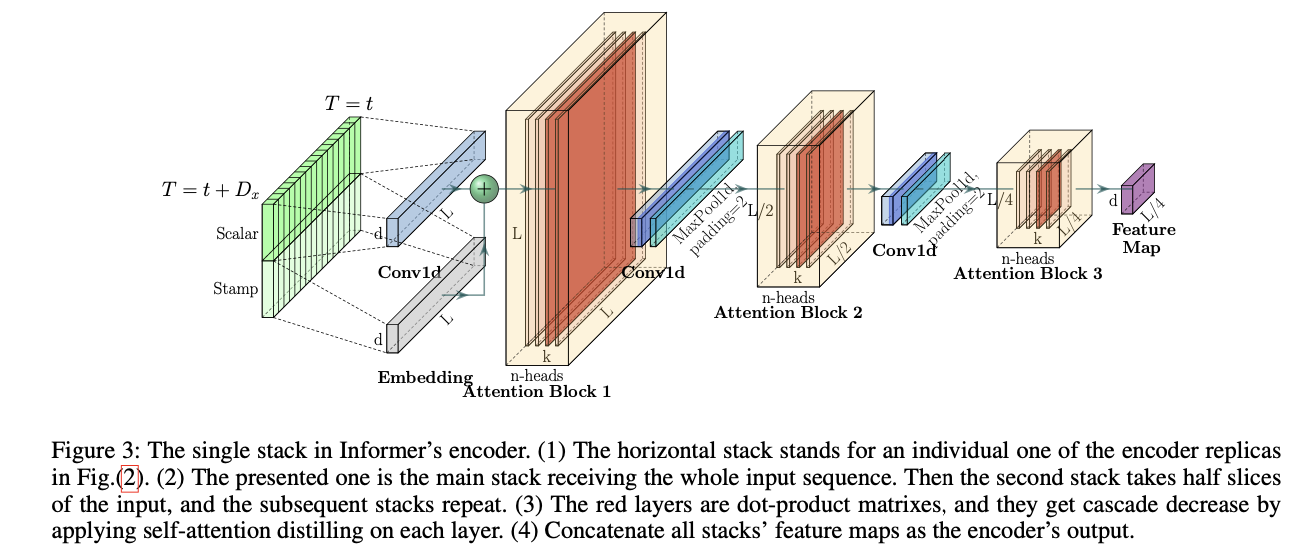
Self-attention Distilling
ProbSparse self-attention 메커니즘의 자연스러운 결과로써, encoder의 feature map은 값의 redundant combinations를 가지고 있다.
Distilling operation을 사용하여 dominating features을 가진 우수한 것들에 우선권을 부여하고 다음 layer에서 focused self-attention feature map을 생성한다. 확장된 convolution서 영감을 받은 “Distilling” 절차는 다음과 같이 j번째 layer에서 (j+1)번째 layer로 나아간다:
여기서 는 attention block을 의미한다.
위 식은 Multi-head ProbSparse self-attention과 필수적인 연산을 포함하고 있으며, Conv1d(·)은 시간 차원에서 1-D convolutional filters(kernel width=3)를 수행하며, ELU(·) 활성화 함수를 사용한다. Stride 2의 max-pooling layer를 쌓고, 원래 크기의 반으로 를 downsampling한다. 이로써 전체 메모리 사용량을 로 줄인다. 여기서 ε는 작은 수이다.
# 코드를 확인하면!
Conv1d >> kernel_size=3, padding=1
maxpool1d >> kernel_size=3, stride=2, padding=1
# 순서는!
# Conv1d -> norm -> activation -> maxPool
# 이렇게 되면 size가 반으로 줄어듦!Replicas of the main stack with halving inputs
Distilling 작업에 견고함을 증가시키기 위해서 input의 절반인 main stack 복제본을 구축하고 Fig(2)처럼 한 번에 한 layer를 떨어트리며 self-attention distilling layer의 수를 점진적으로 줄인다. 따라서, 모든 스택의 output을 합치고 encoder의 최종 hidden representation을 갖는다.
Input의 사이즈를 절반으로 줄인 복제본을 이용해 output을 뽑는다. Input 사이즈를 절반으로 줄였기 때문에, self-attention distilling layer의 수를 줄여줄 수 있다. (distilling layer 하나 당 길이가 반 씩 주니까)
그렇게 나온 여러 outputs들을 합쳐서 최종 hidden representation을 갖는다.
Decoder: Generating Long Sequential Outputs Through One Forward Procedure
Fig(2)의 표준 decoder 구조를 이용하고, 이는 2개의 동일한 multi-head attention layer로 구성되어있다. Generative inference 장기 예측 속도 급락을 완화하기 위해 사용됩니다. 디코더에 다음과 같은 벡터를 공급한다:
where, is the start token,
is a placeholder for the target sequence (set scalar as 0)
Masked multi-head attention은 masked dot-product를 로 설정하여 ProbSparse self-attention 계산에 쓰인다. 이는 각 위치가 이후의 위치에 개입하지 못하게 하여 auto-regressive를 피하게 한다. Fully connected layer는 최종적인 output을 얻고, 그것의 outsize 는 변수가 한 개인 예측을 하는지, 여러 개인 예측을 하는지에 결정된다.
Generative Inference
시작 token은 NLP의 ‘dynamic decoding’에 효율적으로 적용되고, 이를 일반적인 방법으로 확장한다. 토큰으로 특정 flags를 고르는 대신에 output sequence 이전의 slice와 같이 input sequence에서 길이의 sequence를 샘플링한다. 168개의 점 예측을 예로 들면(실험 부분에서 7일의 온도 예측), target sequence 이전의 알고 있는 5일을 “start-token”으로 하고, generative-style inference decoder에 다음을 준다:
는 target sequence의 timestamp 즉, target week의 context를 포함하고 있다. 우리가 제안하는 decoder는 전통적인 encoder-decoder 구조에서 쓰이는 ‘dynamic decoding’이 시간이 걸리는 것과 달리 하나의 forward 절차로 outputs을 예측한다.
Loss function
Target sequence의 prediction에 손실 함수로는 MSE loss function을 선택하고, 손실은 decoder의 출력에서부터 전체 모델을 거쳐 역전파된다.
Experiment 부분은 생략하겠다!
후기
ProbSparse self-attention 부분을 보는데 너무 오랜 시간이 걸렸다. 다른 논문 후기들에서 보았을 때, key를 sampling 하여 dominant queries를 뽑는다고 했는데 내가 논문을 확인했을 땐 그 부분이 잘 보이지 않아서 오래 걸렸던 것 같다.
Proposition 1의 의미를 더 봐보아야 할 것 같다.
코드까지 보면서 열심히 논문을 읽어 본 것은 거의 처음인 것 같은데, 지금은 어렵지만 계속 읽을수록 논문을 읽는 것이 편해질 것을 기대하며...
아직까지는 너무 어렵다..
