Paper review[LLM.int8()]

이상민·2024년 11월 1일

Paper quantization

논문리뷰

목록 보기

17/29

paper : https://arxiv.org/pdf/2208.07339

Abstract

Int 8 matrix multiplication (FFN & attention projection) → Inference 시 메모리 절반으로 줄임(성능 하락 없이)

LLM.int8() : 2부분의 quantization 절차 개발

Matrix multiplication 내 각 inner product에 대해 별도의 normalization constant를 가지고 vector-wise quantization
출현하는 outlier에 대해서는 새로운 mixed-precision decomposition 계획 또한 포함 → 대부분의 값(99.9%의 값)은 8bit로 곱해지는 반면, outlier feature dimension은 16-bit matrix multiplication

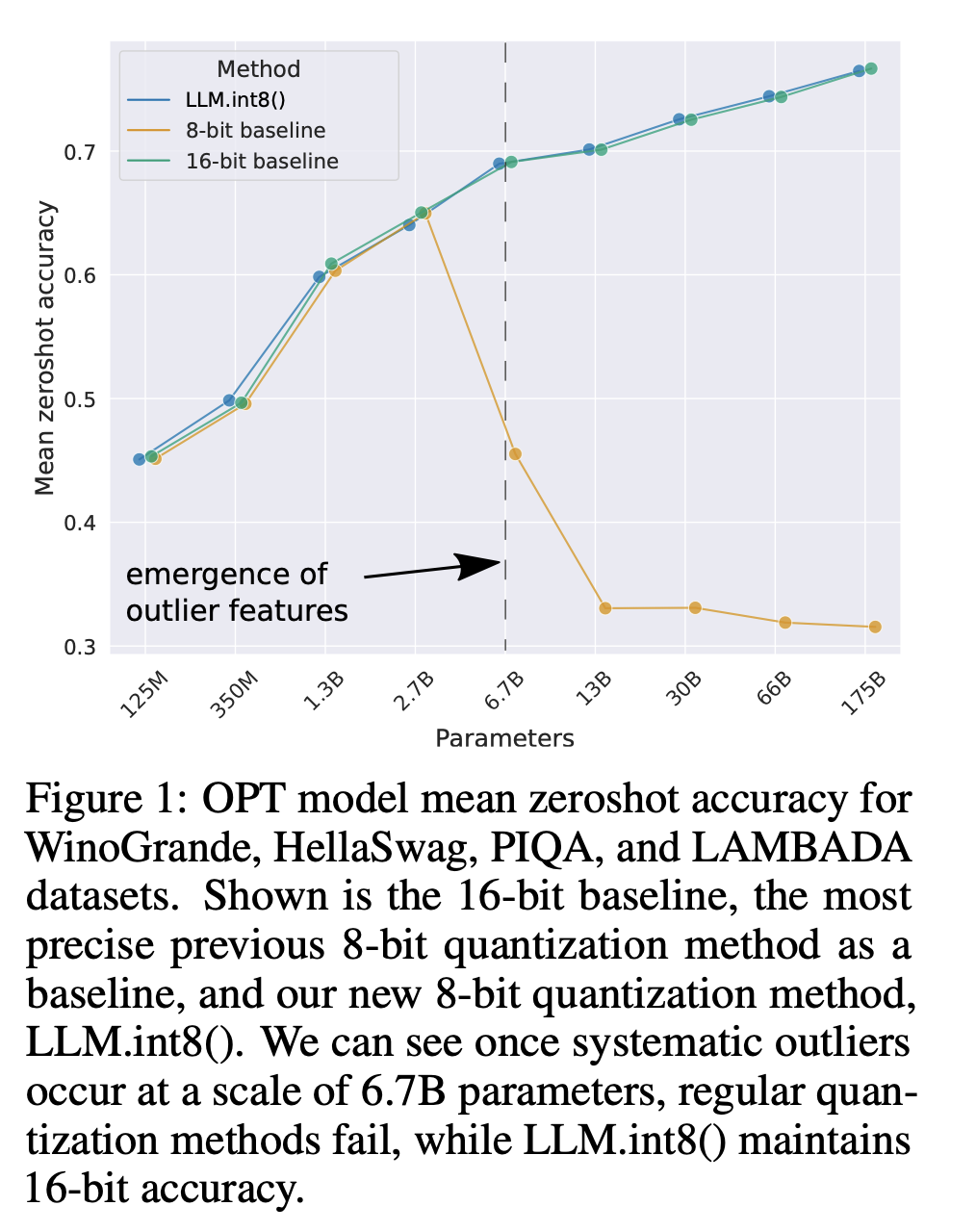
실험적으로 증명 ⇒ 175B 크기의 모델까지 성능 저하 없이 inference 시, LLM int8 사용 가능

1. Introduction

성능 하락 없이 큰 모델들의 quantization: FFN & attention projection layer → 8 bit

2개의 문제를 해결하며 이를 달성:

문제1) 1B 크기가 넘는 모델에서 높은 quantization precision의 필요성
문제2) 6.7B 크기부터 모든 transformer layer에서 한 번 나타나면 quantization precision을 망치는 희소하지만 체계적인 대형 outlier features을 명시적으로 표현할 필요성 → 여기서 체계적인(systematic) 이라는 것은 outlier가 무작위로 생성되는 것이 아니라, 일관되고 예측 가능한 방식으로 생성되는 특성을 지닌다는 의미

Vector Quantization:

의의: 2.7B까지 성능을 유지할 수 있게 함(기존은 350M 이하까지 였음)
설명:
- matrix multiplication을 독립적인 row와 column의 inner product 시퀀스라고 생각 → 각 inner product에서 별개의 quantization normalization constant를 사용(Quantization precision 향상을 위해)
- 계산은 int8로 하고, row와 column의 normalization constant를 이용해서 denormalizing 함으로써 matrix multiplication의 결과 회복 → 회복 후, next operation으로

“Outlier 문제” ⇒ hidden states의 feature dimension(일부 차원) 안에서 극도의 outlier의 출현을 이해하는 것이 중요

설명:
- 6B 크기까지) 큰 feature는 다른 dimension 보다 최대 20배나 크고, transformer layer의 25% 이내에 처음으로 나타난다(층이 12개면, 4층 안에 처음으로 나타남) → 그리고 점차 다른 층으로 뿌려짐
- 6.7B 크기 즈음) ‘모든 transformer layers’ & ‘모든 시퀀스 dimension의 75%’가 극한의 대형 feature에 영향을 받음
  6.7B에서는 outlier가 꽤나 체계적(systematic) : 시퀀스 당 150,000개 outlier 발생 but 전체 transformer에서 오직 6개 feature dimension에 집중되어 있음.
해결:
- 1)
  - Outlier feature dimension을 0으로 setting(outlier feature는 전체 input feature에 0.1%정도를 차지함) → top-1 attention softmax probability mass가 20% 이상 감소 & validation perplexity가 약 600-1000% 감소
  - Random하게 feature dimension 0으로 setting(feature dimension의 수는 똑같이 둠) → probability가 최대 0.3% 감소 & perplexity 약 0.1% 감소
  - 결과: outlier feature dimension을 0으로 setting 하는 것이 결과에 중요한 영향을 끼침
- 2)
  - Mixed-precision decomposition
  - Outlier feature dimension : 16-bit matrix multiplication
  - 다른 feature dimension(99.9%) : 8-bit matrix multiplication

LLM.int8() : Vector Quantization + Mixed-precision decomposition

의의: 175B LLM까지 성능 하락 없이 inference 가능
특징
- 오픈 소스: Software를 open-source로 공개
- 사용: 모든 hugginface 모델에 적용할 수 있도록 huggingface transformers와 통합 → linear layer가 있는 huggingface model에서 논문의 메서드를 사용할 수 있음

2. Background

의문점 2개:

‘어떤 크기에서 quantization 실패?’, ‘왜 quantization 기술은 실패?’
이들은 quantization precision에 어떤 연관이 있나?

이 질문에 답하기 위해 공부해야 할 것들:

Asymmetric quantization (zeropoint quantization) → 높은 precision but 실질적인 제약 때문에 거의 사용되지 않음
Symmetric quantization (absolute maximum quantization) → 가장 많이 사용되는 기술

Absmax quantization

설명: 입력을 8bit 범위([-127, 127])로 scaling.
방법: 입력에 $s_{x_{f16}}$ 을 곱함. $s_{x_{f16}}$ : 127 / 전체 텐서에서 max 값( $\max(\text{input})$ )
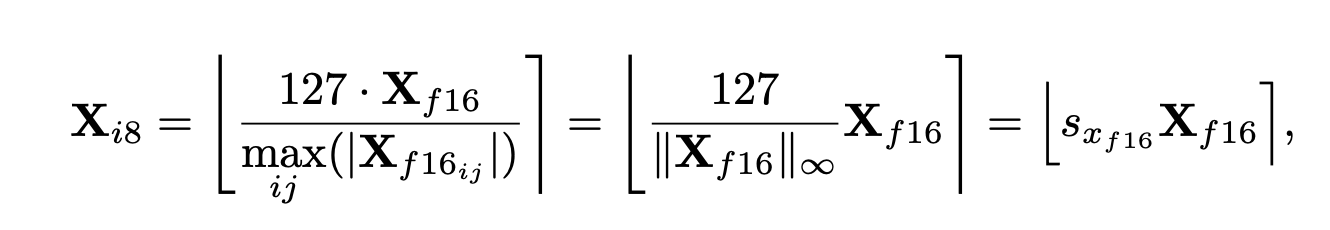
$\lfloor \rceil$ : 근처 integer로 반올림

Zeropoint quantization

설명: 입력 분포를 전체 범위 [-127, 127]로 이동
방법: Normalized dynamic range( $nd_x)$ 로 scaling → zeropoint( $zp_x)$ 로 이동 (즉, 크기를 맞춰주고, 0 기준으로 대칭이 되게 맞춰줌)

단점: matrix multiplication에서 int16의 계산이 지원되지 않으면 계산 시간이 오래 걸릴 수 있음.
예시) $zp_{a_{i16}}, zp_{b_{i16}}$ 와 함께 zeropoint quantized numbers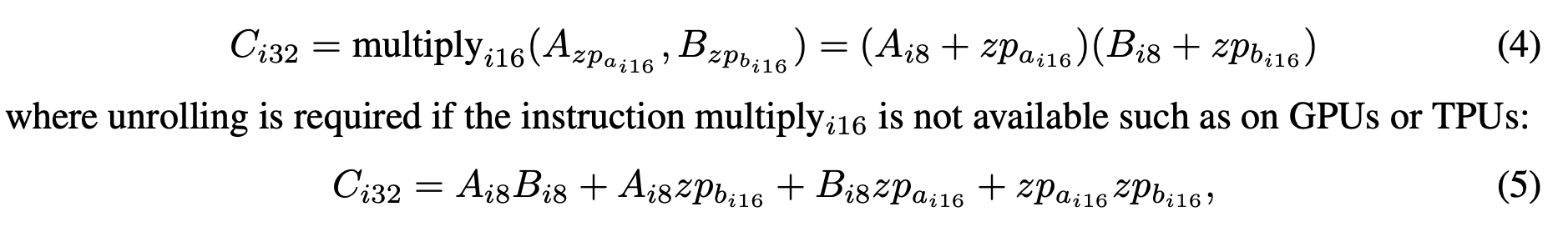 $A_{i8}, B_{i8}$ 계산
$\text{multiply}_{i16}$ 가 안되면, 수식을 다음과 같이 풀어서 계산해야 하기에 시간이 오래 걸릴 수 있다( $A_{i8}, B_{i8}$ 은 int8 precision으로 계산될 수 있지만, 나머지 부분은 int16/32 precision으로 계산됨)
그리고 quantized 된 채 나온 결과 $C_{i32}$ 를 scaling constant $nd_{a_{f16}}, nd_{b_{f16}}$ 으로 나눠주어 dequantize 해줘야 한다(int → float. dequantized: 이산적 데이터 → 연속적 데이터) → 최종적인 데이터 형태: f16

Int8 Matrix Multiplication with 16-bit Float Inputs and Outputs

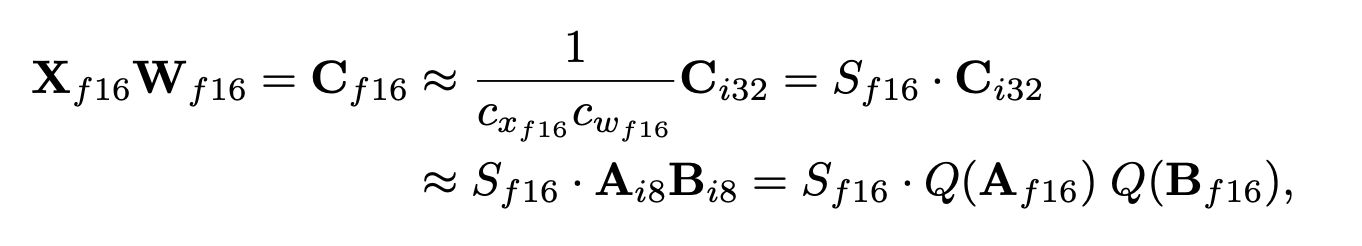
여기서) $c_{x_{f16}}, c_{w_{f16}}$

absmax quantization의 경우: 각각 tensor-wise scaling constants $s_x, s_w$
zeropoint quantization의 경우: 각각 $nd_x, nd_w$

(이해가 안가는 점: 만약 quantizaiton 방법으로 absmax quantization을 사용했으면 $C_{i32}$ 는 나오지 않을텐데. 저렇게 표현한 이유를 모르겠다 → 왜냐하면 zeropoint-quantization의 경우 shifting에서 int16부분이 생겨 최종 결과가 int32로 표현되지만, absmax quantization은 그렇지 않기 때문)

흐름 설명) zeropoint-quantization 중심

원래 같으면 X(type:FP16) W(type:FP16) → C(type:FP16)
Zeropoint-quantization을 사용하면 결과값으로 C(int32)가 만들어지고, 이를 다시 돌려놓기 위해 dequantization으로 $c_{x_{f16}}, c_{w_{f16}}$ 를 나눠준다.
$\frac{1}{c_{x_{f16}}c_{w_{f16}}} = S_{f16}$ 으로 표기한 것 (S : scaling factor)
$C_{i32}$ 는 $Q(A_{f16}) Q(B_{f16})$ 으로 표현할 수 있음. 그래서 최종적으로 위와 같이 표현되는 것임

3. Int8 Matrix Multiplication at Scale

Tensor 당 하나의 scaling constant를 사용 → 하나의 outlier가 모든 다른 value들의 quantization precision을 낮출 수 있음

⇒ 해결 방안) Vector-wise quantization

6.7B 이상의 큰 모델의 모든 transformer layer에서 발생하는 넓고 큰 outlier feature을 다루기에 vector-wise quantization은 충분하지 않음

⇒ 해결 방안) mixed-precision decomposition (outlier(약 0.1%) : 16-bit precision, others(약 99.9%) : 8-bit precision)

3-1 Vector-wise quantization

Matrix multiplication에서 scaling factor의 수를 늘리는 방법 중 하나 : matrix multiplication을 독립적인 inner product의 시퀀스로 보는 것

Hidden state $\textbf{X}_{f16} \in \R^{b \times h}$ , weight matrix: $\textbf{W}_{f16} \in \R^{h \times o}$ 에 대하여, $\textbf{X}_{f16}$ 의 각 row에 서로 다른 scaling constant( $c_{x_{f16}}$ ), $\textbf{W}_{f16}$ 의 각 column에 서로 다른 scaling constant( $c_{w_{f16}}$ )을 부여.

Dequantization : Inner product result(int8 계산 결과)에 scaling constant( $\frac{1}{c_{x_{f16}}c_{w_{f16}}}$ )로 denormalize 함으로써 할 수 있음.

전체 matrix multiplication은 outer product( $c_{x_{f16}} \otimes c_{w_{f16}}$ )로 denormalization 하는 것과 동일

(이유: $c_{x_{f16}} \in \R^b, c_{w_{f16}} \in \R^{o}$ 이니까, $c_{x_{f16}} \otimes c_{w_{f16}} \in \R^{b \times o}$ . $X_{f16}W_{f16} \in \R^{b \times o}$ )

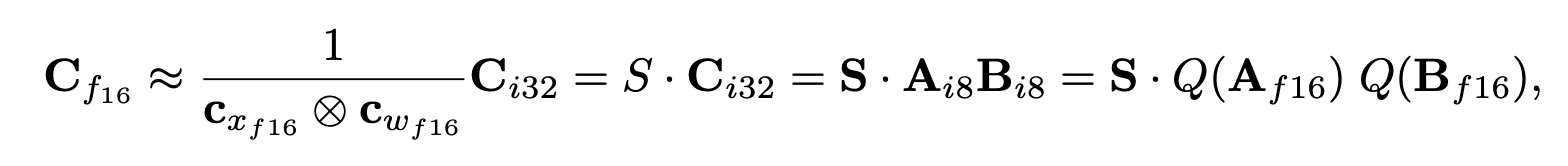
의문점)

수식에 대한 의문
Absmax-quantization: FP16 → scaling factor(FP16) x Int8
그렇기에 matmul 계산: $\frac{1}{s_x \otimes s_w} X_{\text{int} 8}W_{\text{int} 8} \rightarrow \frac{1}{s_x \otimes s_w}C_{i16}$
위와 같은 형태가 되어야 하지 않나? 왜 $C_{i32}$ 가 수식에 나와있는지 모르겠다.

[해당 의문에 대해 나중에 이해한 바]
int8 x int8 element의 계산 결과값은 int16으로 표현될 수 있다. 하지만 matmul은 i번째 row와 j번째 column elements의 곱의 총 합이다. 모든 결과값을 더해주는 과정에서 int16의 범위를 넘을 수 있다. 그래서 int32로 표현하는 것 같다.

"Zeropoint-quantization에서 shifting에 사용되는 zeropoint는 왜 int16으로 표현이 되는가?"
& "Round(fp16 * fp16) 인데 왜 굳이 int16으로 표현이 되는가?"

여기서 굳이 quantzation 시키기 위해서 zeropoint도 int16으로 바꿨다면, 그니까 int형에 맞게 표현하고 싶은데 해당 범위에 최대한 비슷한게 int16이라서 그렇게 맞췄다고 생각하는 것이 맞을까?
근데 zeropoint를 구하는 식에서 min 값을 사용한다고 하더라도(fp16 * min(fp16)) 이라도 int16으로 표현할 수 있는 범위를 넘어갈 수 있지 않은가? 이런 경우는 생각하지 않아도 되는 것인가? X값의 요소가 30000을 넘고 하지 않으니까?..?

참고) fp16의 범위 [−65504, 65504]

이 부분은 zeropoint를 표현할 때, 이를 int type으로 가장 잘 표현할 수 있는게 int16이라서 이렇게 quantization 한 것이라고 생각하고 넘어가기로 했다..

3-2 The core of LLM.int8(): Mixed-precision Decomposition

배경:
- vector-wise quantization은 outlier feature에 효과적이지 않음
- Outlier features가 sparse(약 0.1%) & systematic 하다는 것을 발견 → decomposition 기술 개발을 할 수 있게 해줌
- Input matrix $\text{X}_{f16} \in \R^{s \times h}$ 에서 outliers는 체계적으로 모든 sequence dimension $s$ 에서 발생하지만, 특정 feature/hidden dimension $h$ 에서는 제한적으로 나타난다는 것을 발견
방법:
- Input matrix $\text{X}_{f16} \in \R^{s \times h}$ 에 대해 outlier feature dimension을 set $O = \{i | i \in Z, 0 \leq i \leq h\}$ 로 분리 → outlier를 하나라도 포함하고 있는 $h$ 의 모든 차원(threshold $\alpha$ 로 판단. 논문에서는 6.0→ 성능 하락이 거의 0이기에 6.0을 threshold로 두기에 충분함)
- 즉, input의 column을 기준으로 보았을 때, 해당 column의 요소 중 하나라도 threshold를 넘는 것이 있다면, 해당 column은 outlier set으로 빼서 16-bit 계산을 해줌. 그렇지 않은 것은 8-bit 계산을 해줌 → 그리고 해당 값들을 더함(outlier set이나 others set이나 출력 크기가 같음. Hidden state들만 떼어 왔기 때문에 출력 크기가 변하진 않음)
- 수식(Einstein notation):
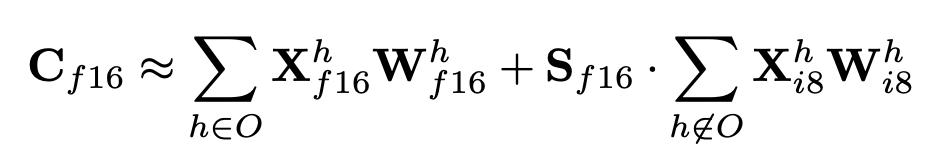
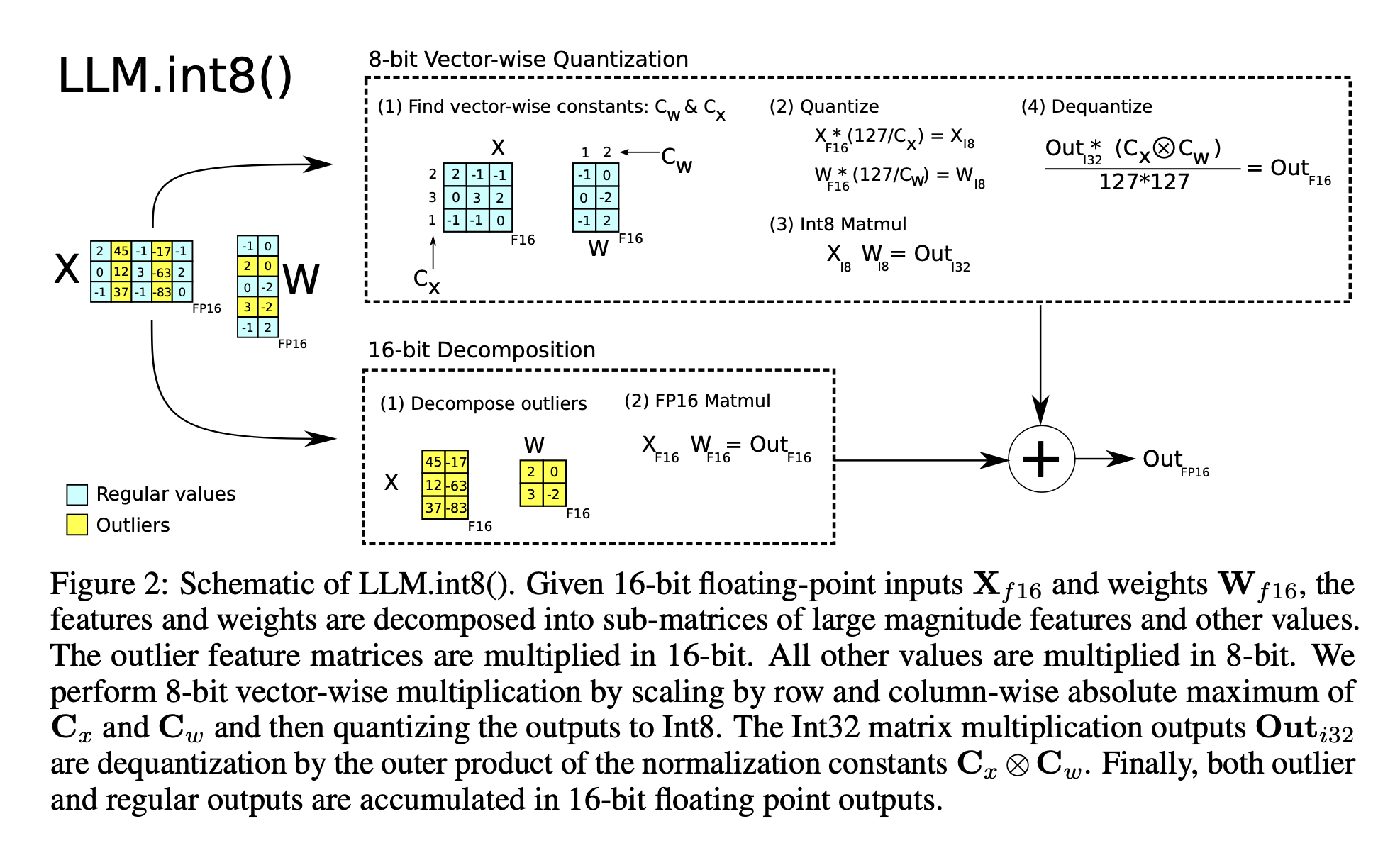
- 방법은 아래 그림을 참고하면 이해하기 좋음

3-4 Main Results of the Experiments

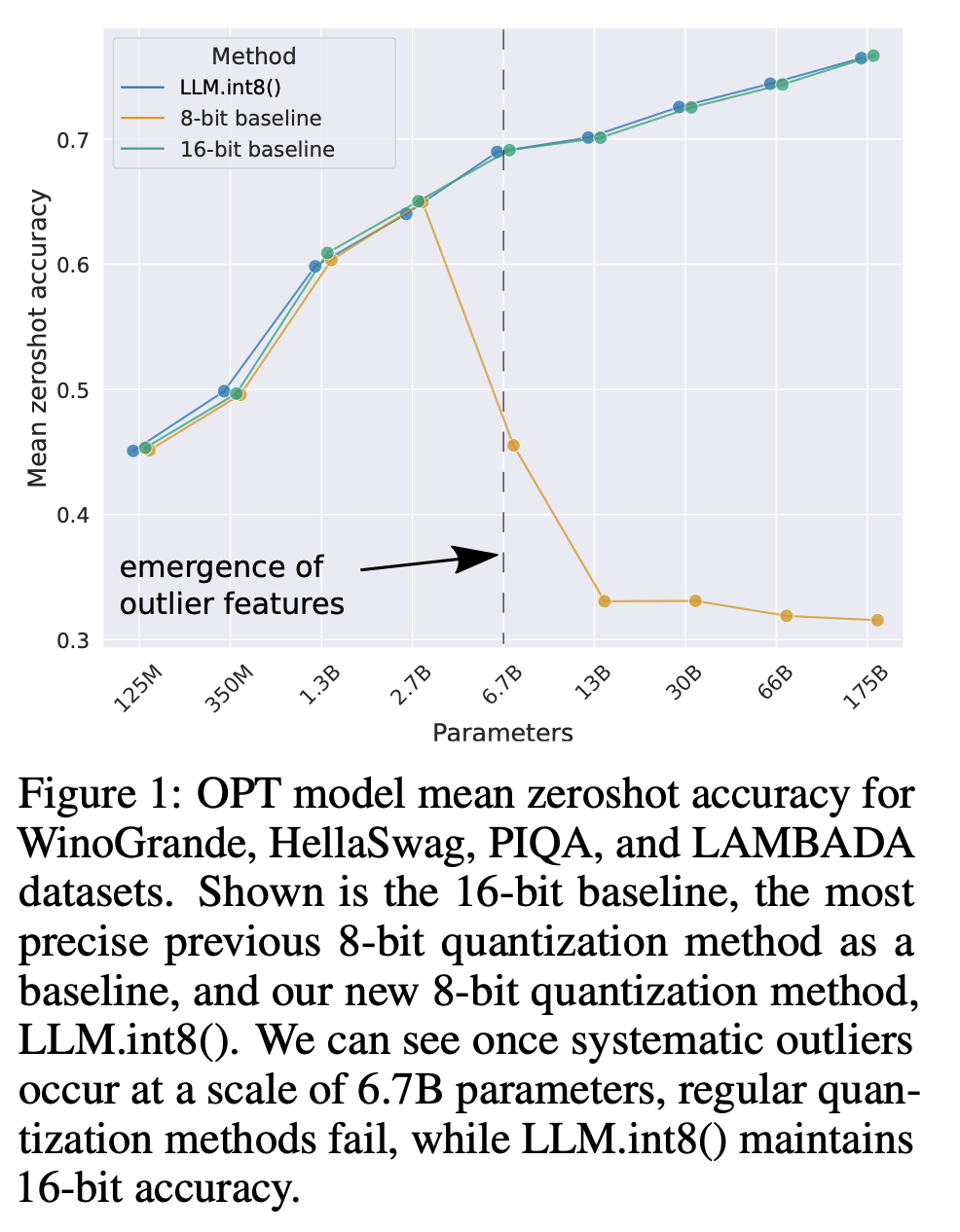
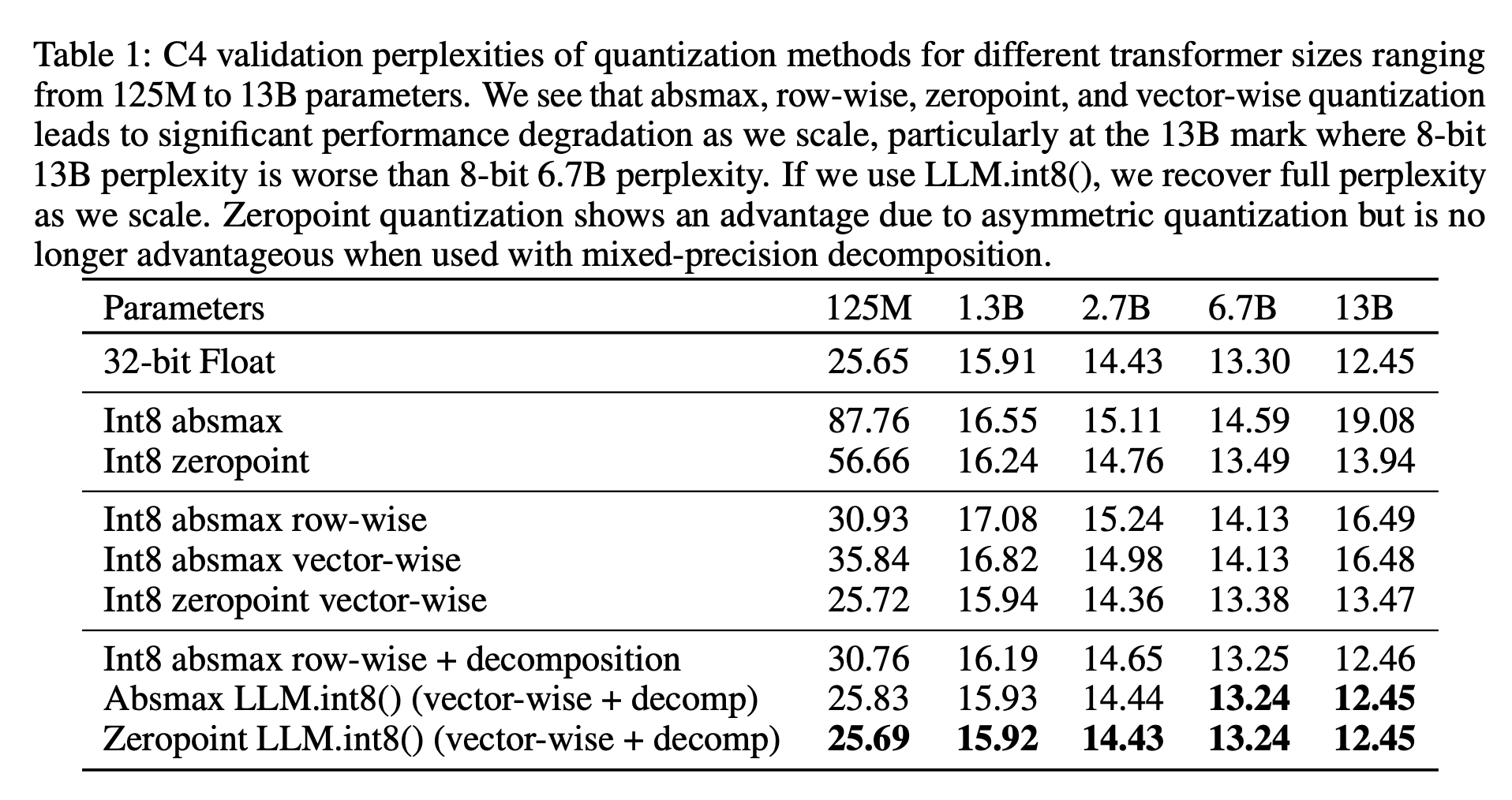
4. Emergent Large Magnitude Features in Transformers at Scale

Outlier features는 attention과 전체적인 transformer의 예측 성능에 강한 영향을 미침
13B model의 경우, 2048 토큰 시퀀스 당 최대 150k개의 outlier 존재하지만, outlier features는 매우 systematic 하고 거의 7개의 unique feature dimension에서만 나타남

4-1 Finding Outlier Features

분석을 위한 목표)

‘결과가 이해하기 쉽고 복잡하지 않음’
‘중요한 확률적이고 구조화된 패턴을 포착’

해당 특징을 띄는 small subset of features 선택이 목표.

Outlier 기준)

magnitude of feature ≥ 6.0
적어도 layer의 25%에 영향을 줘야 함
적어도 시퀀스 dimension의 6%에 영향을 줘야 함

더 formally 하게)

기호 설명: $X_l \in \R^{s \times h}, l \in 0, \dots, L$ , $s :$ 시퀀스 dimension, $h :$ feature dimension

Magnitude가 6.0 이상인 value를 하나 이상 가지고 있음 → 해당 dimension $h_i$ 추적
모든 transformer layer의 적어도 25%에서 outlier가 same feature dimension $h_i$ 에서 발생 → 통계 수집
모든 hidden state $X_l$ 전반에 걸쳐, 전체 시퀀스 dimension $s$ 의 적어도 6%에는 나타남 → 통계 수집

6 Discussion and Limitations

의의)

성능 하락 없이 Inference 메모리 요구량 감소
Inference 시, 성능 하락 없이 quantization을 사용할 수 있는 모델의 크기를 175B까지 늘림

한계)

연구를 오직 int8로만 진행함 → FP8로는 하지 않음
연구를 오직 175B model까지만 진행해봄 → 그 이상 규모의 모델에서는 추가적인 특성이 나타나 논문의 quantization 방법을 망칠 수 있음
연구에서 Int8 multiplication을 attention function에서 사용하지 않음
Inference에만 초점을 두었지, 학습이나 finetuning은 연구하지 않았음(int8 training)