배경지식

---

Morpology 는 이미지를 구조적이고 기하학적인 특징을 기반으로 분석하고 처리하는 기법입니다. 주로 이진화된 이미지나 그레이스케일 이미지를 대상으로 특정 구조를 강조하거나, 불필요한 노이즈를 제거하거나, 원하는 영역을 추출하는 데 사용됩니다. 이 글에서는 이진화된 이미지의 morpology 만을 다룹니다.

집합 용어

• $f(x, y)$ : 디지털 이미지의 픽셀 값을 나타냅니다. 여기서 $x$ 와 $y$ 는 픽셀의 좌표입니다.

• $A, B$ : Binary image 에서 픽셀 값이 1인 좌표들의 집합입니다. 즉, binary image 를 좌표 집합으로 표현한 것입니다.

• $w = (x, y)$ : 픽셀 좌표 $(x, y)$ 로 정의되는 집합의 한 원소입니다.

• $w \in A$ : $w = (x, y)$ 가 집합 $A$ 의 요소임을 나타냅니다. 즉, 특정 좌표 $(x, y)$ 가 $A$ 에 속해 있음을 뜻합니다.

• $B = \{w|condition\}$ : $B$ 는 특정 조건을 만족하는 모든 $w$ 로 구성된 집합을 의미합니다.

주로 대문자는 좌표들의 집합, 즉 binary image 를 의미하고 소문자는 대문자 집합 내에서 특정 좌표를 나타내는 원소를 의미합니다.

Translation

집합 안의 모든 원소들을 벡터 $z$ 만큼 이동시키는 연산입니다.

위 수식은 집합 $B$ 에 있는 모든 원소 $b$ 에 벡터 $z$ 를 더한 새로운 좌표들의 집합인 $(B)_z$ 를 만듭니다.

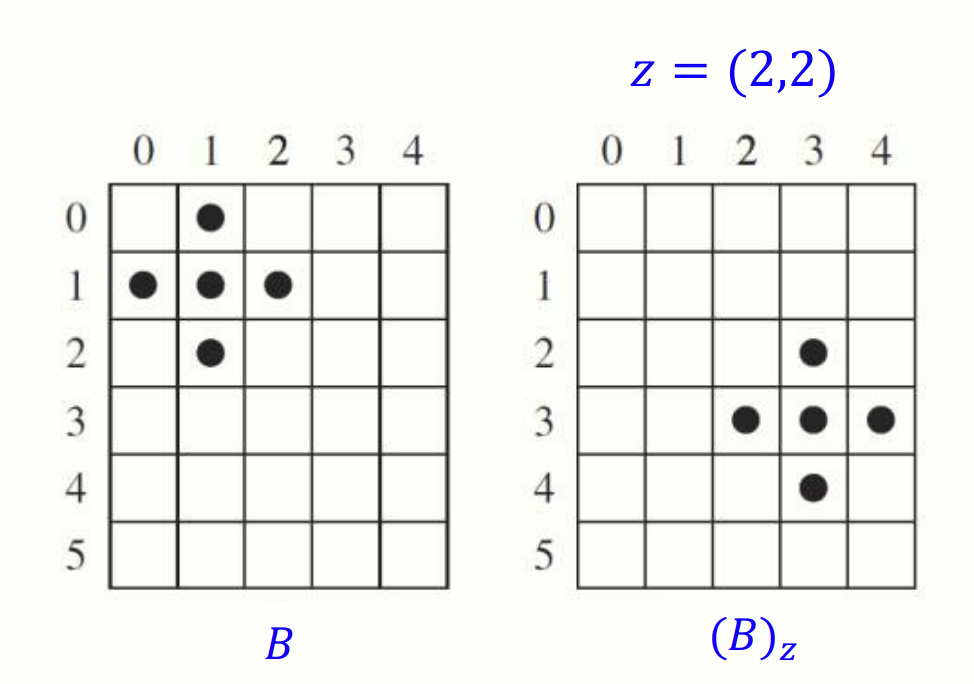
모든 검은 점들이 (2, 2) 만큼 이동했다.

Reflection

집합 안의 모든 원소들을 원점에 대해 대칭시키는 연산입니다.

위 수식은 원점을 기준으로 $B$ 의 모든 점을 대칭 이동시킵니다. $b = (b_1, b_2)$ 라면 reflection 된 점은 $(-b_1, -b_2)$ 가 됩니다.

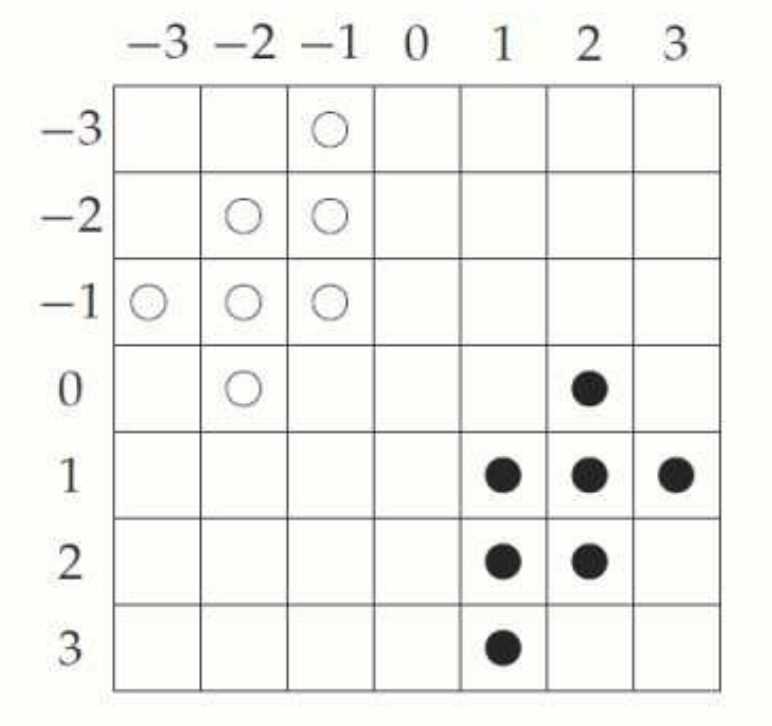
흰 점과 검은 점이 원점을 기준으로 대칭이다.

논리 연산 기반

Morpology 연산은 binary image 에서 논리 연산(AND, OR 등) 을 기반으로 수행됩니다. 예를 들어, 두 픽셀 집합을 비교하거나 겁치는 영역을 평가합니다.

입력 binary image($A$) 와 구조 요소(Structuring Element, SE) 가 연산의 주요 구성 요소입니다.

SE 와 Origin

SE 는 origin(원점 혹은 중심점) 을 기준으로 입력 이미지 위에서 이동하며 연산을 수행합니다. 기본적으로 원점은 SE 의 중앙에 위치합니다(특별히 명시되지 않는 한).

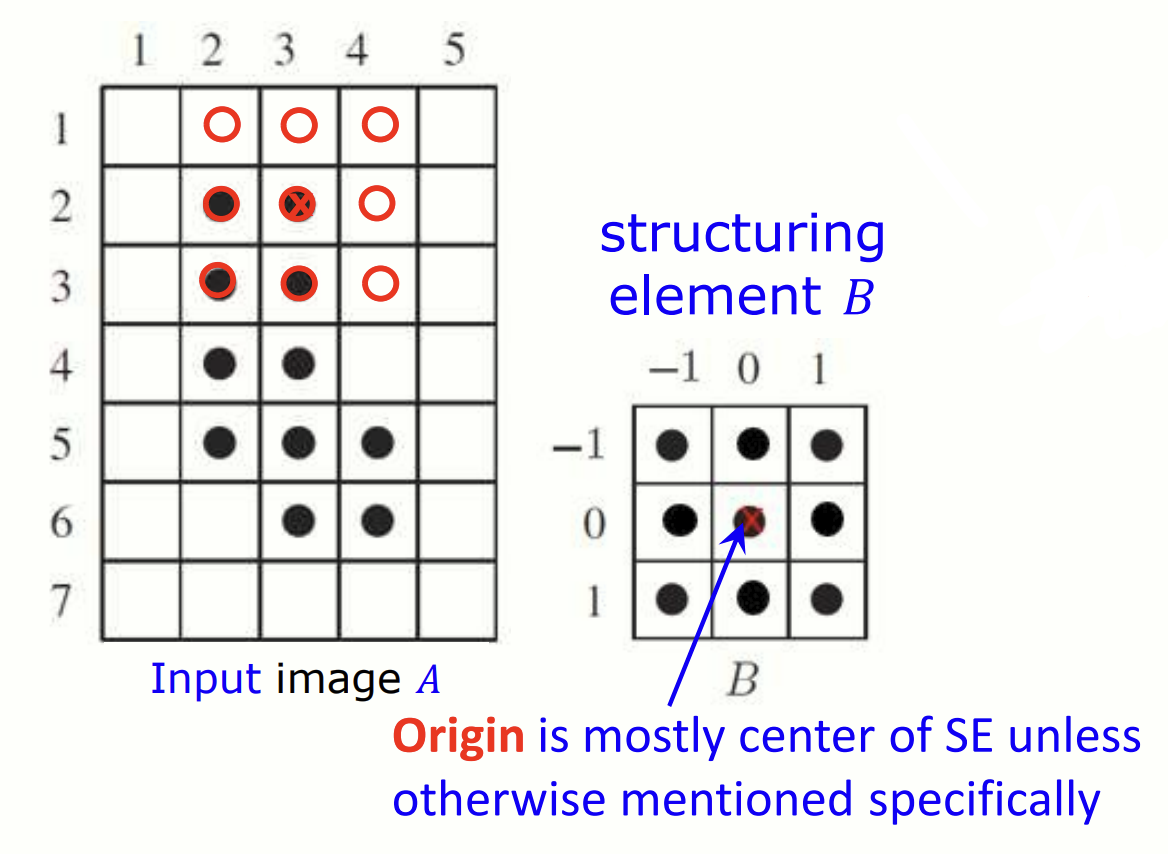
3x3 size 의 SE 가 A 위에서 이동 중이다. 특정 영역에 대해 조건이 만족되면 출력 이미지를 갱신할 것이다.

Output pixel 의 결정

SE 의 origin 이 입력 이미지 $A$ 의 특정 픽셀에 겹쳐지면, SE 와 입력 이미지가 논리적으로 평가되어 해당 픽셀의 출력 값이 결정됩니다. 출력은 $w$ 에서 계산되며, SE 가 입력 이미지 위에 놓였을 때의 결과입니다.

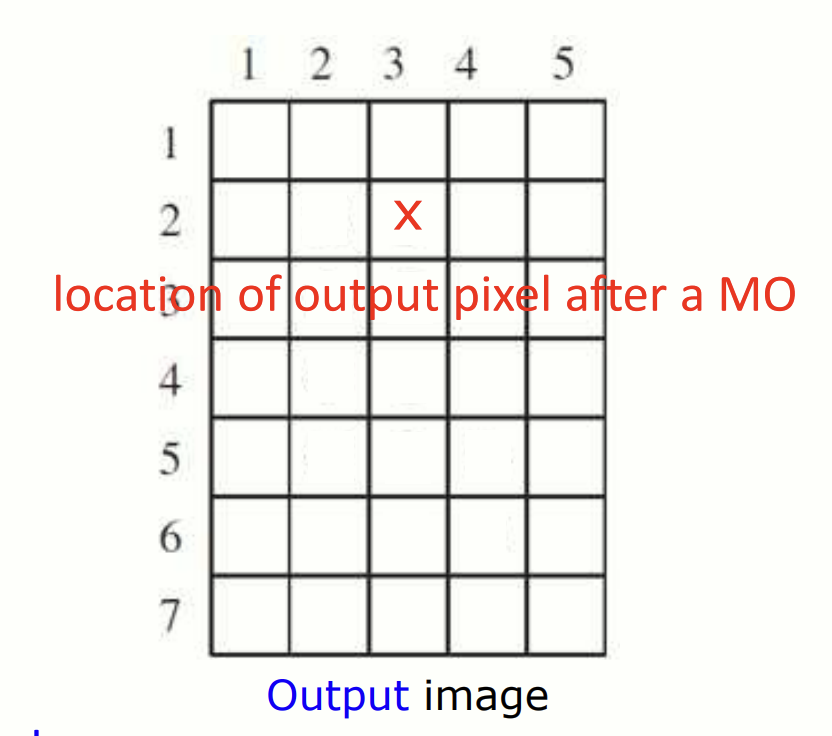
특정 연산 결과로 X 에 표시된 출력 값이 생성된다. 출력 이미지는 입력 이미지와 SE 의 연산 결과로 만들어진 binary image 이다.

Erosion & Dilation

---

Dilation(팽창)

Dilation 은 morpology 연산 중 하나입니다. Dilation 은 binary image 에서 SE 를 사용하여 입력 이미지를 확장하거나 영역을 넓히는 연산입니다.

Dilation 은 다음과 같이 정의됩니다:

• $\hat{B}$ : SE(B) 의 reflection
• $(\hat{B})_z$ : SE 를 $z$ 좌표만큼 translation 한 결과
• 이 연산은 $\hat{B}$ 가 입력 이미지 $A$ 의 어떤 부분이라도 겹친다면, 출력 이미지의 해당 위치를 1로 설정합니다.

Dilation 에 사용되는 SE 는 대체로 대칭적인 형태를 가집니다($B = \hat{B}$)

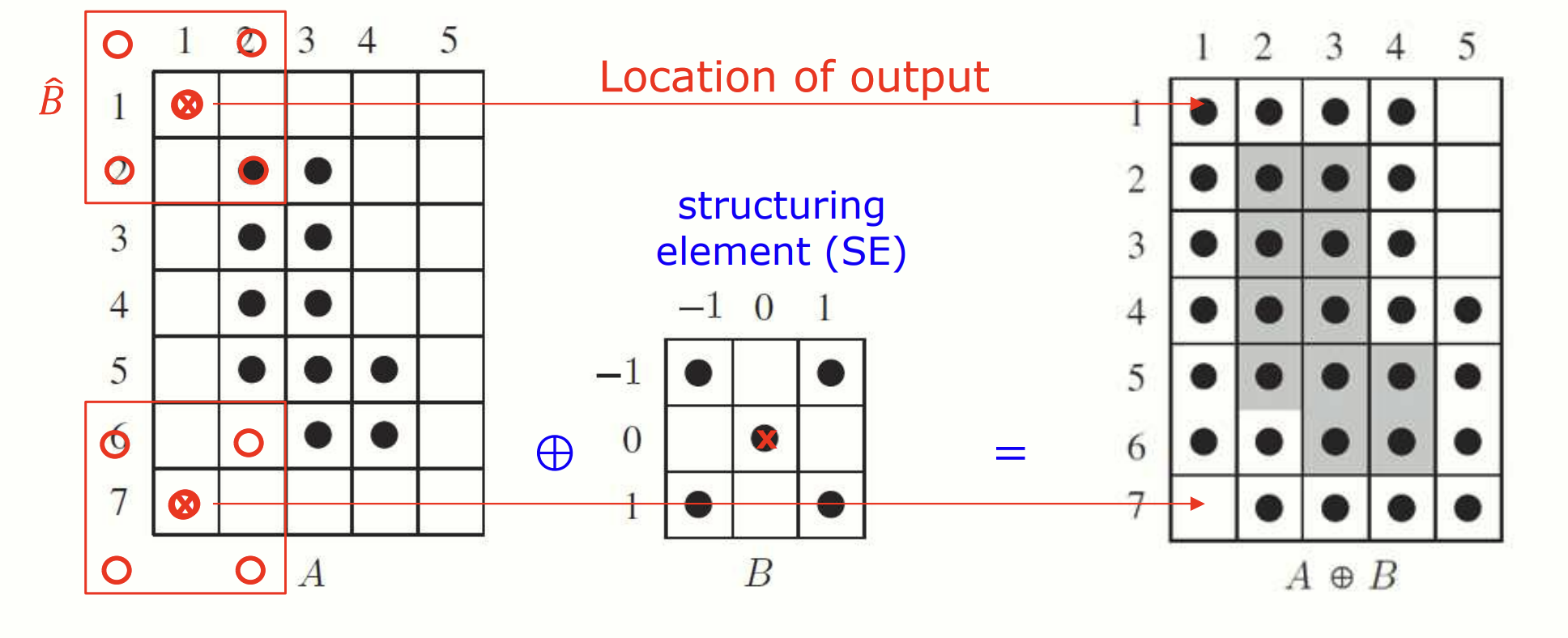
A 와 B 가 단 한 점이라도 겹치면 origin 을 1로 처리한다.

구현

skimage.morphology.binary_dilation

• skimage 에서 제공하는 dilation 연산 함수
• footprint: SE 를 정의하는 매개변수
• mode: 경계 처리 방식. 'min'으로 설정하면 경계의 최소값으로 채운다.

from skimage.morphology import binary_dilation as bwdilate
A = plt.imread('morph_txt.png')  # 입력 이미지
B = np.ones((3, 3))  # 3x3 크기의 SE
D = bwdilate(A, footprint=B, mode='min')  # Dilation 수행

Erosion(침식)

Erosion 은 객체의 외각을 줄이거나 제거하는 데 사용되는 morphology 연산입니다. 입력 이미지 $A$ 에서 SE 인 $B$ 가 겹치는 부분을 평가하며, $B$ 의 모든 픽셀이 $A$ 와 겹쳐야 출력값이 1이 됩니다.

Erosion 은 다음과 같이 정의됩니다:

$B$ 를 입력 이미지 $A$ 위에서 움직이며, $B$ 의 모든 요소가 $A$ 에 포함되는 경우에만 해당 픽셀 값을 1로 설정합니다.

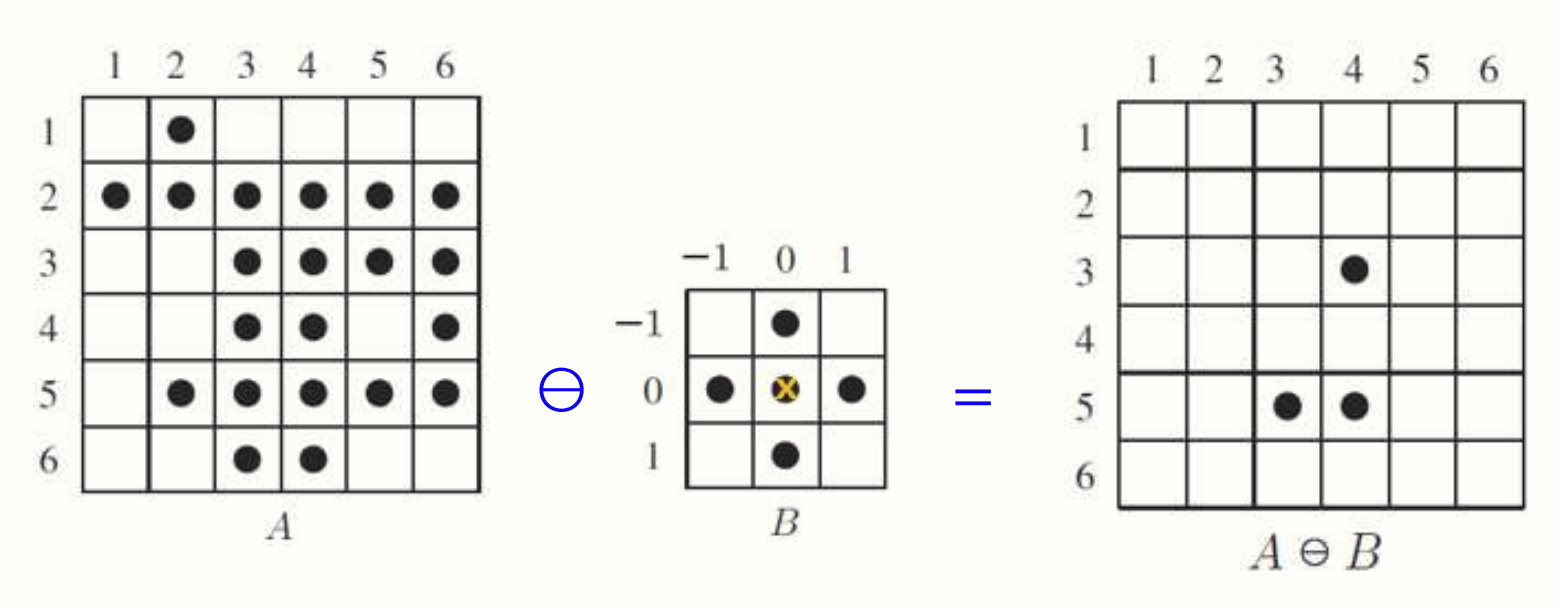
구현

from skimage.morphology import binary_erosion as bwerode

• skimage 라이브러리에서 제공하는 binary erosion morphology 연산 함수
• 이미지에서 SE 를 사용하여 erosion 처리를 수행한다.

from skimage.morphology import binary_erosion as bwerode

A = plt.imread('rings.png')  # 입력 이미지
B = np.ones((3, 3))  # 3x3 크기의 SE

E = bwerode(A, footprint=B, mode='min')  # Erosion 수행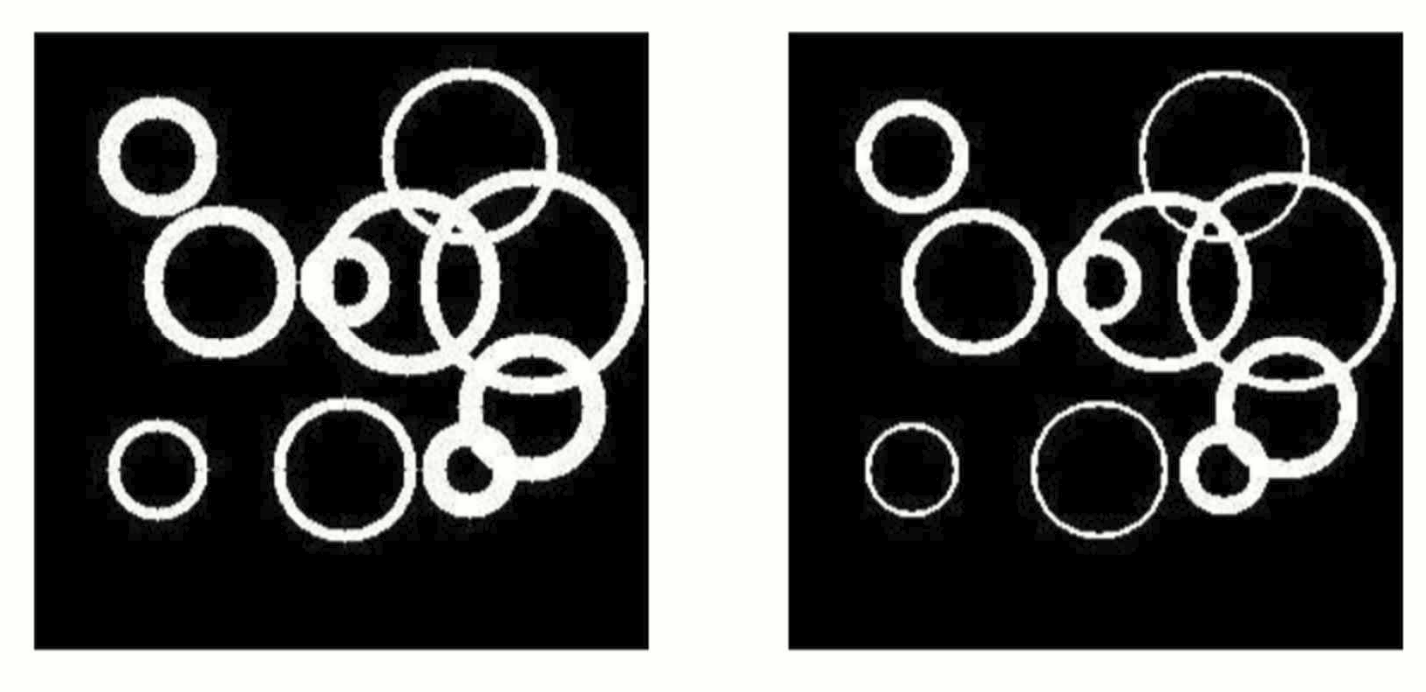

Erosion 후 객체의 선이 얇아졌다.

경계 추출

Dilation 과 erosion 을 적절히 수행하여 객체의 경계를 추출할 수 있습니다.

내부 경계 추출

• 입력 이미지 $A$ 에서 erosion 연산($A \ominus B$) 결과를 빼면 내부 경계만 남게 됩니다.

• Erosion 은 객체의 외곽을 줄이므로, $A$ 와의 차이는 경계에 해당합니다.

구현

n = io.imread('pinenuts.png')  # 이미지를 불러옴
p = ~((n > 130) & (n < 165))  # Binary segmentation
pe = bwerode(p, footprint=sq, mode='min')  # Erosion 연산 수행
p_int = p - pe  # 내부 경계 추출

외부 경계 추출

• 입력 이미지 $A$ 를 dilation ($A \oplus B$) 한 결과에서 원본 이미지를 빼면 외부 경계만 남습니다.

• Dilation 은 객체의 외곽을 확장하므로, 확장된 부분과 $A$ 의 차이가 외부 경계입니다.

구현

# 내부 경계 추출 구현 코드와 이어짐
pd = bwdilate(p, footprint=sq, mode='min')  # Dilation 연산 수행
p_exp = pd - p

Morphological Gradient

• Dilation 과 erosion 결과의 차이를 계산하여 객체의 전체 경계(내부 + 외부)를 추출합니다.

• 객체의 전체 외곽선이 강조됩니다.

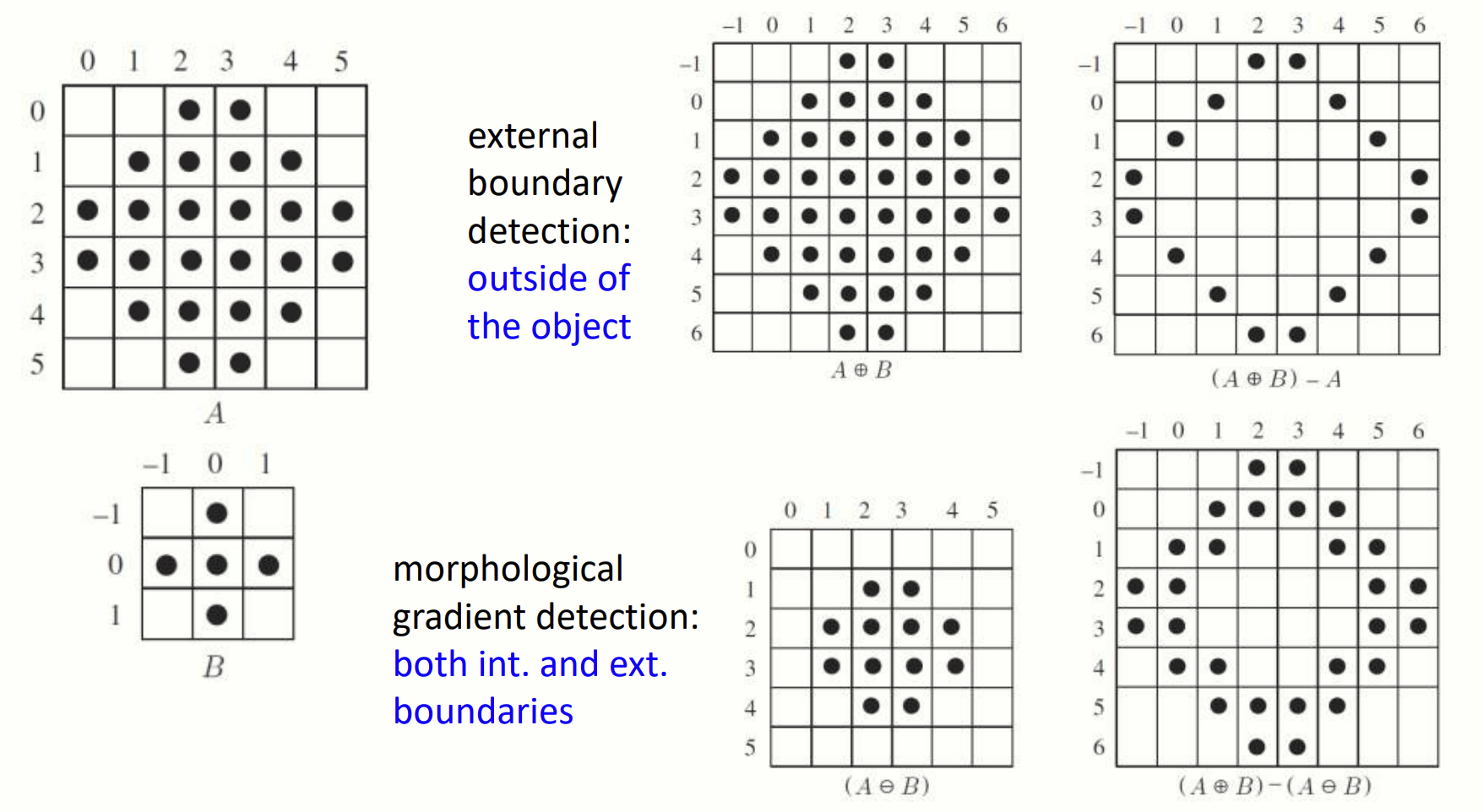
외부 경계 추출, morphological gradient.

구현

# 외부 경계 추출 구현 코드와 이어짐
# pd 와 pe 는 반드시 boolean 에서 int 나 float 으로 변경되어있어야 함
p_grad = pd - pe  # Morphological gradient 추출

Opening & Closing

---

Opening

Opening 은 erosion 후 dilation 을 순차적으로 적용하는 morphology 연산입니다. Opening 은 다음과 같이 정의됩니다:

• $A$ : 입력 이미지
• $B$ : SE
• $A \ominus B$ : Erosion 연산
• $(A \ominus B) \oplus B$ : Erosion 결과에 dilation 연산을 적용한 것

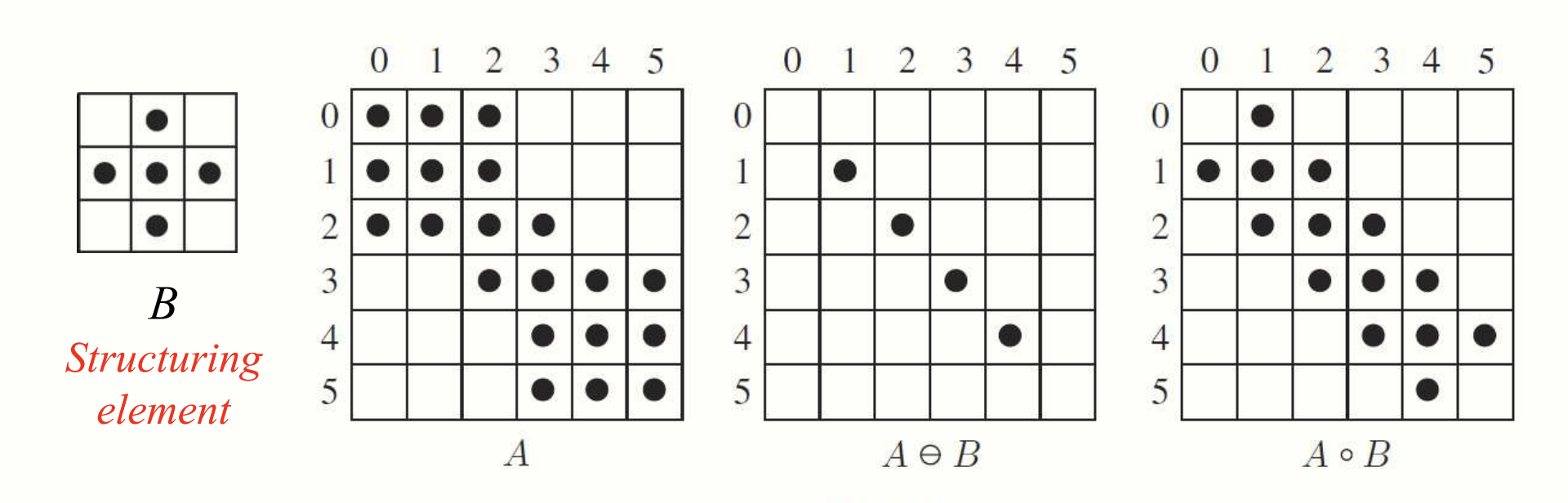
Opening 연산 예시.

Opening 연산은 작은 객체(noise)를 제거하거나, 객체 사이의 좁은 연결부를 분리하는 데 사용됩니다. Erosion 을 통해 작은 영역을 제거한 뒤, dilation 으로 객체의 크기를 다시 복구합니다.

Opening 의 속성

1. 포함 관계

• Opening 결과는 항상 입력 이미지 $A$ 의 부분집합입니다.
• Erosion 으로 인해 객체가 줄어들기 때문에 입력 이미지를 포함할 수 없습니다.

2. 멱동성(Idempotent)

• Opening 연산을 여러 번 반복해도 결과는 동일합니다.
• 즉, 첫 번째 연산 이후 추가 opening 연산은 영향을 주지 않습니다.

3. 포함 관계 확장

• $A$ 가 $C$ 의 부분집합이면, opening 결과 $A \circ B$ 도 $C \circ B$ 의 부분집합이 됩니다.

4. 이미지 처리 효과

• 이미지에서 객체의 외곽선을 부드럽게 만듭니다(smoothing).

• 좁은 연결부를 제거하여 객체를 분리합니다.

• 객체의 불필요한 돌출부를 제거합니다.

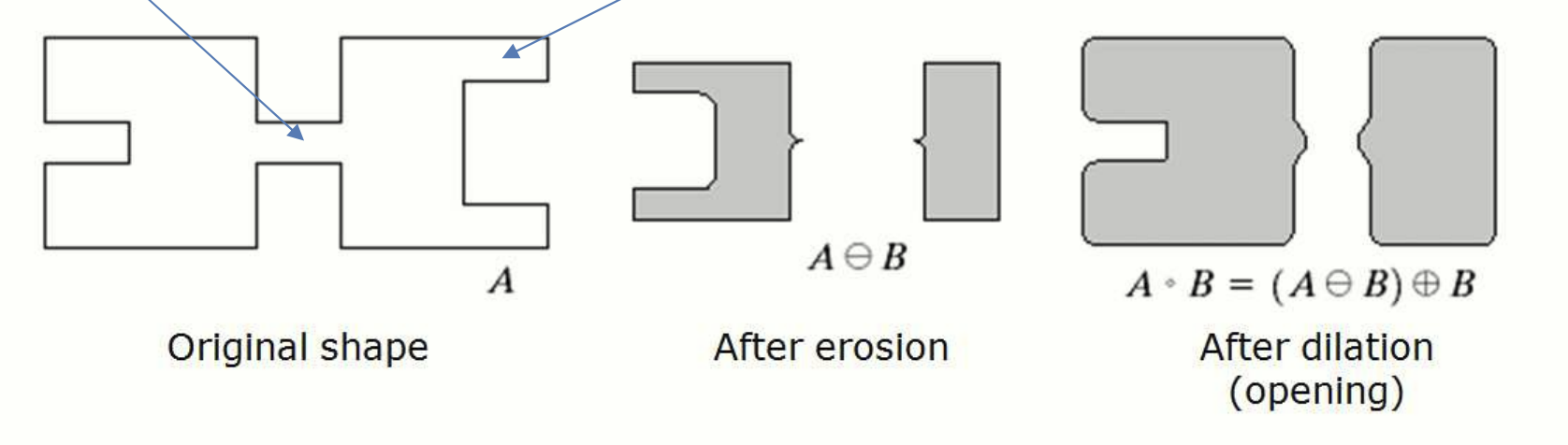
Opening 예시 1.

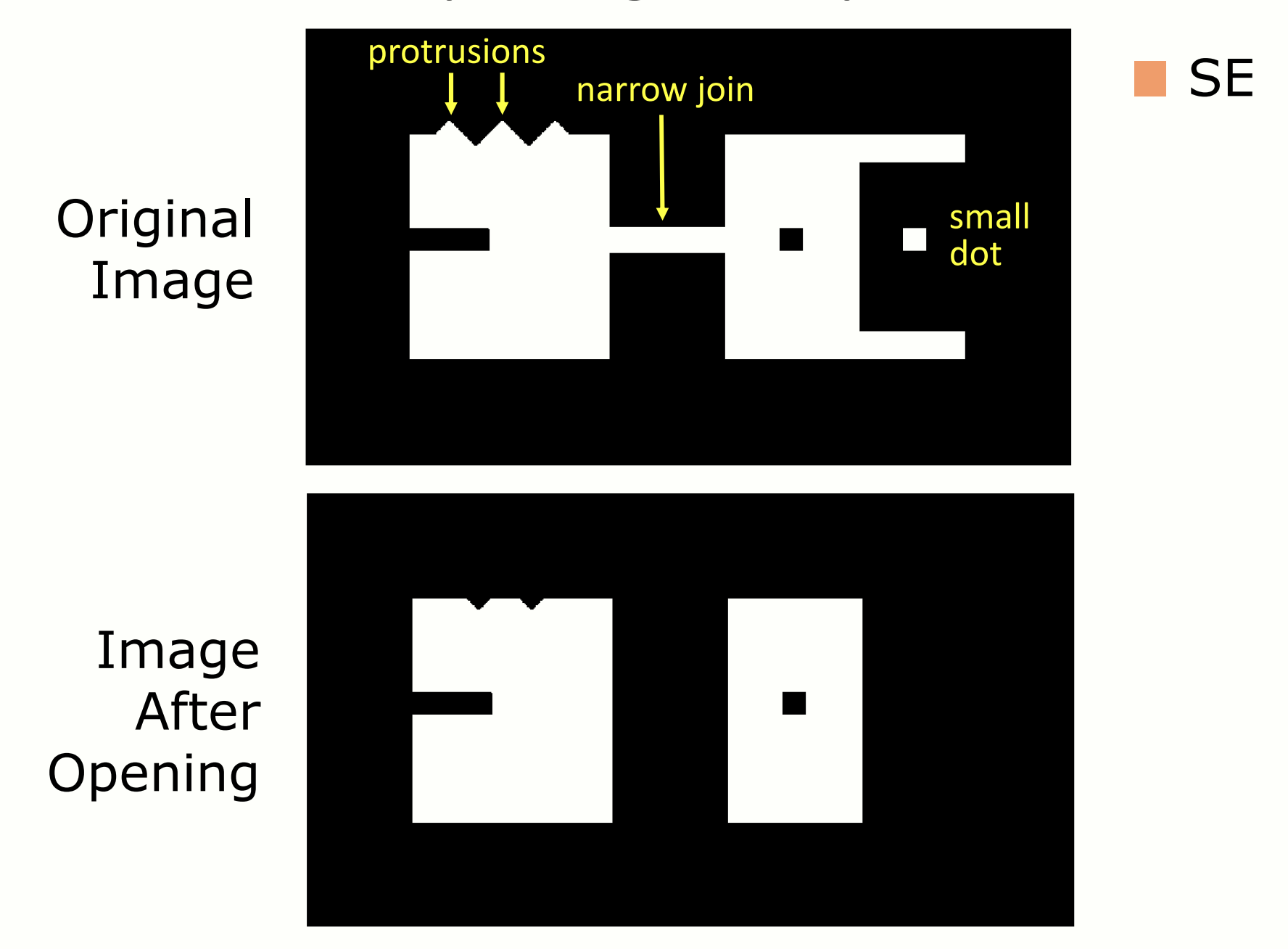
Opening 예시 2.

Closing

Closing 은 dilation 후 erosion 을 순차적으로 수행하는 morphology 연산입니다. Closing 연산은 다음과 같이 정의됩니다:

• $A$ : 입력 이미지
• $B$ : SE
• $A \oplus B$ : Dilation 연산
• $(A \oplus B) \ominus B$ : Dilation 결과에 erosion 연산을 적용한 것.

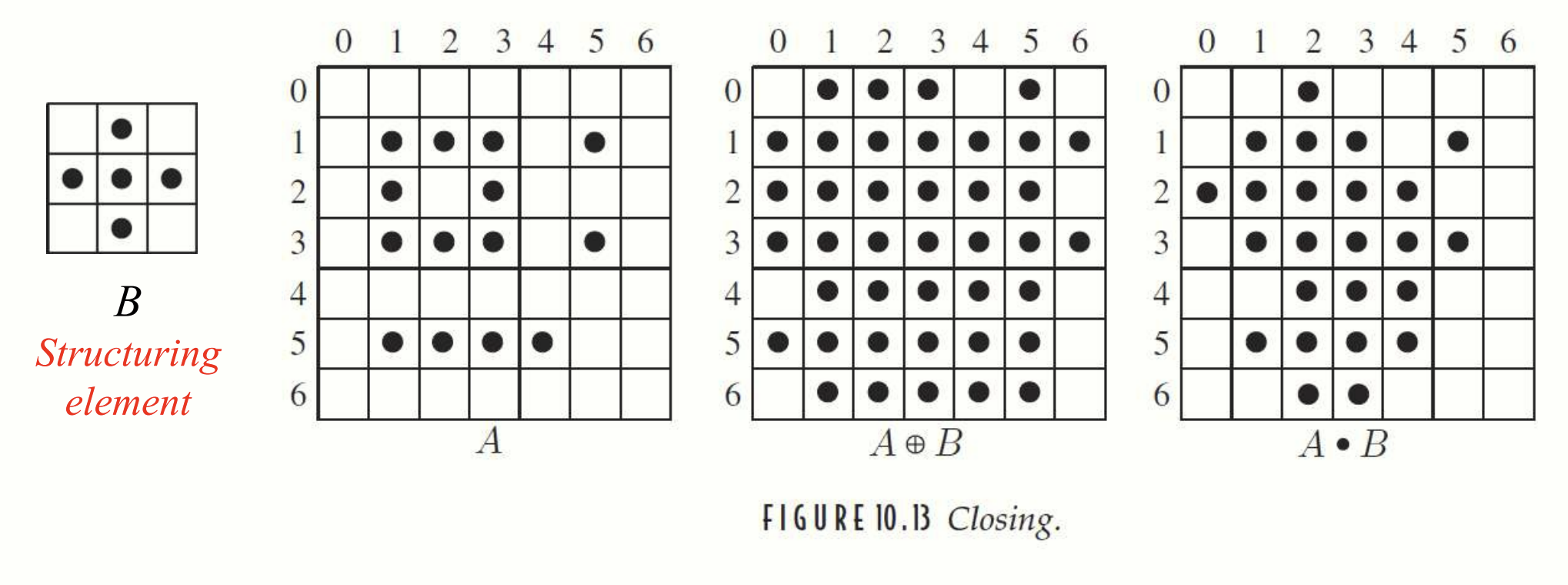
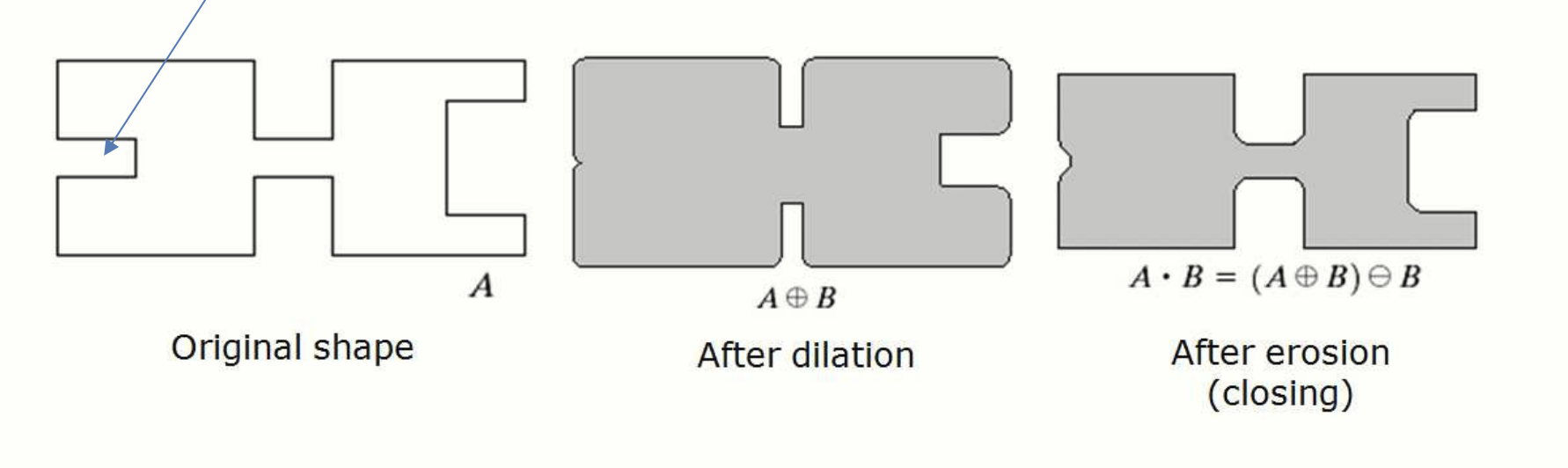
Closing 연산 예시.

Closing 연산은 객체의 내부 빈 공간을 채우고, 끊어진 객체를 연결하는 데 유용합니다. Dilation 으로 빈 공간을 메우고, erosion 으로 외곽선을 복구합니다.

Closing 의 속성

1. 포함 관계

• Closing 결과는 항상 입력 이미지 $A$ 를 포합합니다.
• Dilation 으로 객체가 확장되기 때문에, 원래 이미지의 모든 픽셀이 유지됩니다.

2. 멱동성(Idempotent)

• Closing 연산을 여러 번 반복해도 결과는 동일합니다.
• 첫 번째 연산 이후 추가 연산은 영향을 주지 않습니다.

3. 포함 관계 확장

• $A$ 가 $C$ 의 부분집합이면, closing 결과 $A \bullet B$ 도 $C \bullet B$ 의 부분집합이 됩니다.

4. 이미지 처리 효과

• 객체 외곽선을 부드럽게 만듭니다.
• 좁은 틈이나 끊어진 객체를 연결합니다.
• 객체 내부의 작은 빈 공간을 제거합니다.

Clsoing 예시 1.

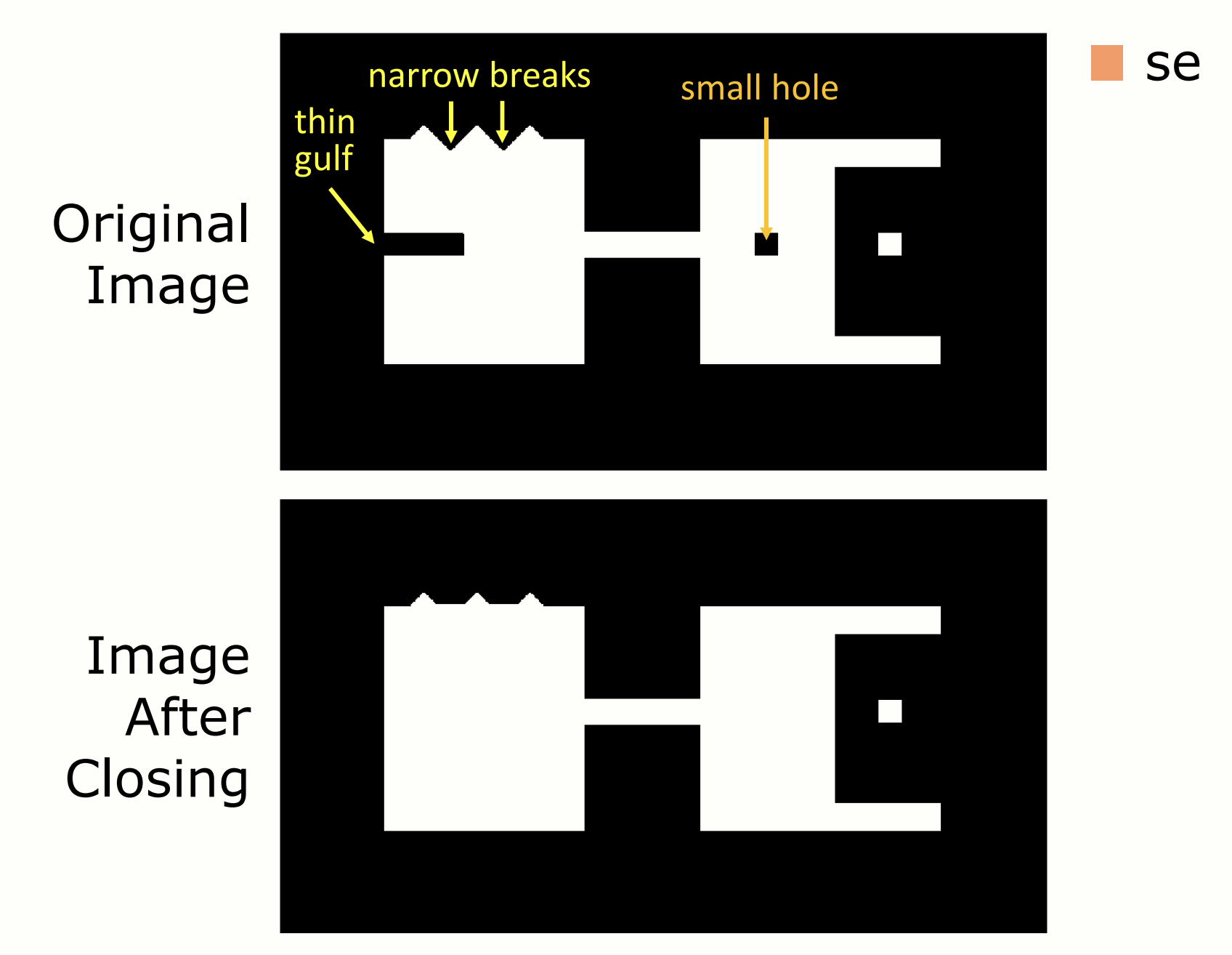
Closing 예시 2.

Opening & Closing 구현

사례 1

from skimage.morphology import binary_closing as bwclose
from skimage.morphology import binary_opening as bwopen

B_cr = np.array([[0,1,0], [1,1,1], [0,1,0]])  # 십자 모양 SE
B_sq = np.ones((3,3))  # 3x3 크기의 SE

test = np.zeros((10,10))  # 10x10 크기의 binary test image
test[1:6,1:4] = 1  # 왼쪽의 큰 사각형
test[2:5,5:9] = 1  # 오른쪽의 큰 사각형
test[7:9,3:8] = 1  # 아래쪽의 긴 사각형
test[3,5] = 1  # 노이즈 점

test_open = bwopen(test, footprint=B_cr, mode='min') * 1  # 십자 모양 SE(B_cr)을 사용하여 opening 연산 수행

test_close = bwclose(test, footprint=B_cr, mode='min') * 1  # 십자 모양 SE(B_cr)을 사용하여 closing 연산 수행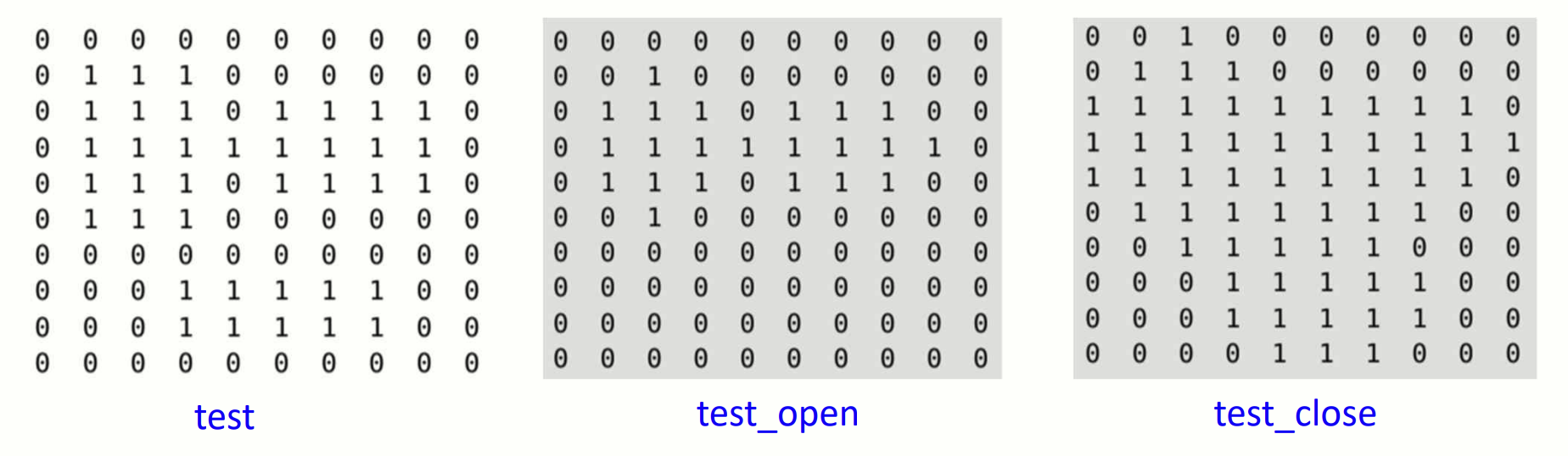

Opening 후 noise 점(단일 픽셀)이 제거되었다. 좁은 연결부가 분리되어 객체 간격이 늘어났다. 반면 closing 후 객체 내부의 빈 공간이 메워졌고, 끊어진 객체 간 좁은 틈이 연결되었다.

사례 2

# 테스트를 위해 입력 이미지에 노이즈 추가
img = plt.imread('circles.png')  # 입력 이미지 읽기
A = img.astype('bool') * 1  # Binary image 로 변환
x = np.random.random_sample(A.shpae)  # 임펄스 노이즈 생성
A[np.nonzero(x > 0.95)] = 0  # 배경에 랜덤하게 흑점 noise 추가
A[np.nonzero(x <= 0.05)] = 1  # 객체에 랜덤하게 백점 noise 추가

# Opening 후 Closing
A_f1 = bwclose(bwopen(A, footprint=B_sq, mode='min'), footprint=B_sq, mode='min')  # 정사각형 SE 사용
A_cf2 = bwclose(bwopen(A, footprint=B_cr, mode='min'), footprint=B_cr, mode='min')  # 십자형 SE 사용

흑점과 백점 noise 를 원본 이미지 전반에 무작위로 분포시켰습니다. 정사각형 SE 를 사용한 결과 객체 내부의 작은 검은 점 noise 가 제거되었습니다. 십자형 SE 는 내부의 검은 점을 완벽하게 제거하지는 못했지만, 객체의 외곽선이 더 부드럽게 정리되었습니다.

Hit-or-Miss Transform

---

Hit-or-Miss transform 은 한 이미지에서 같은 모양을 탐지(shape detection)하는데 유용한 기법입니다. Hit-or-Miss transform 의 수학적 정의는 다음과 같습니다:

• $A$ : 입력 이미지
• $B_1, B_2$ : SE
• $\overline{A}$ : A의 차집합 혹은 보수(complement)

핵심 아이디어

입력 이미지에서 $B_1$ 과 같은 모양을 가지는 부분을 찾습니다. $B_2$ 는 $A$ 의 배경에서 $B_1$ 주변 조건을 설정합니다. 두 개의 SE 를 사용해 $A$ 와 $\overline{A}$ 각각에 erosion 연산을 수행한 뒤 교집합을 취합니다.

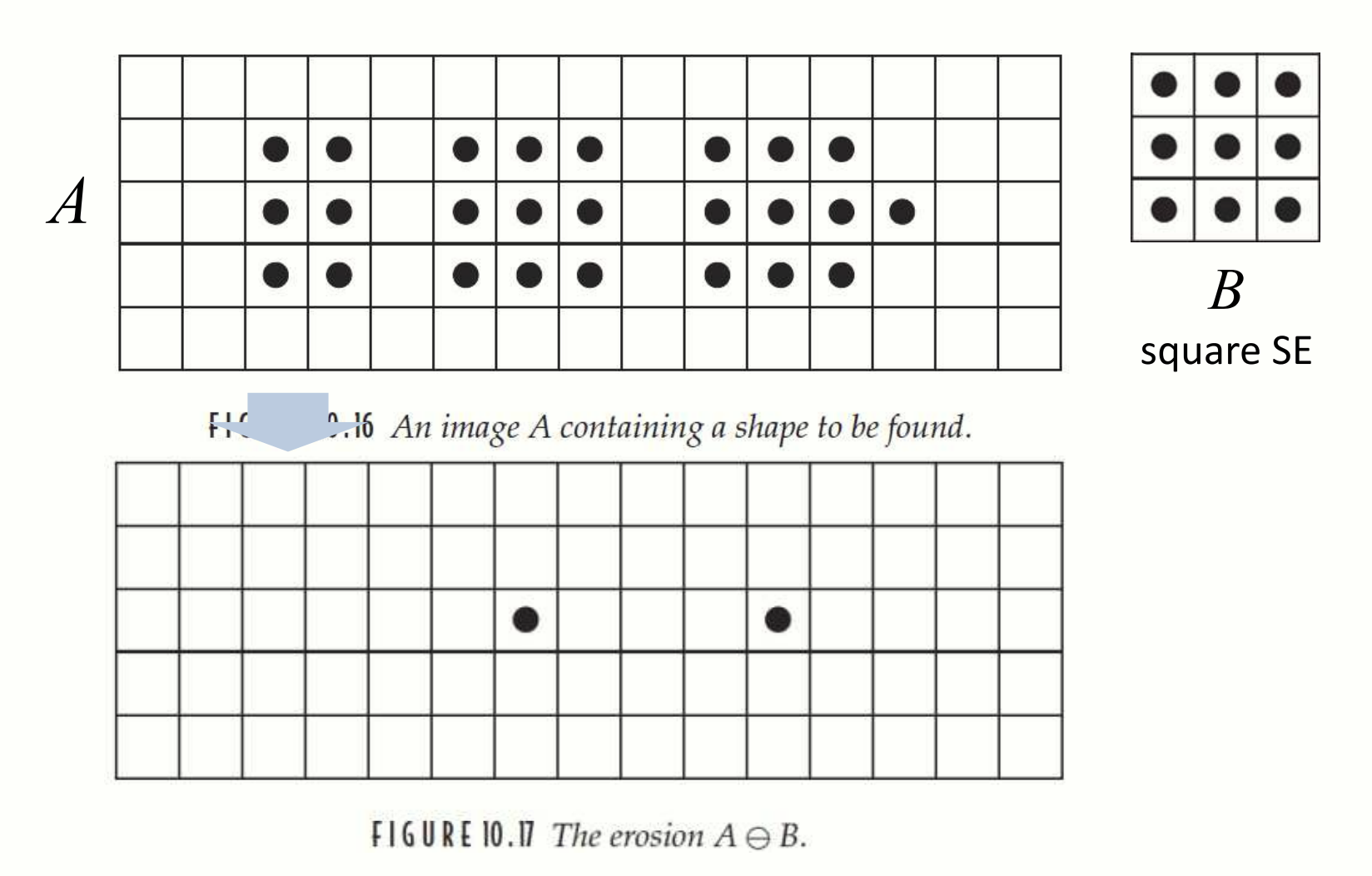
A 에서 첫번째 SE 인 B 를 erosion.

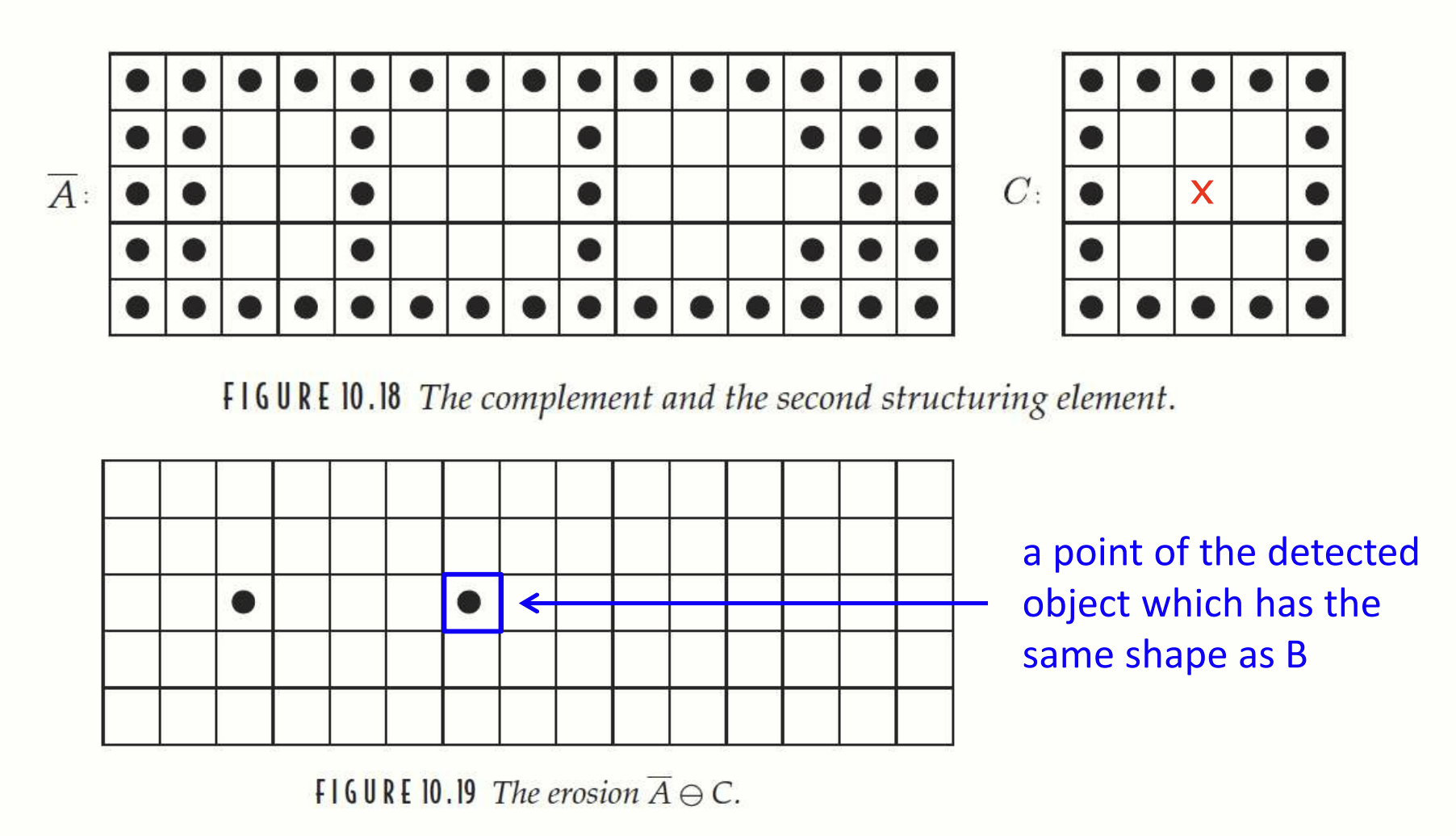
A 의 차집합에 두번째 SE 인 C 를 erosion.

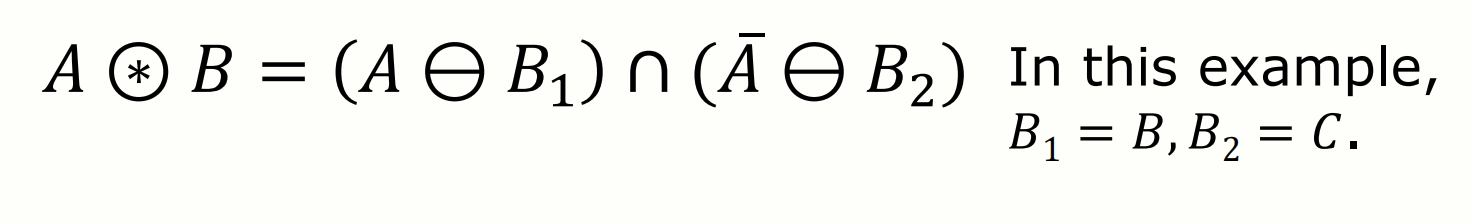
두 SE 의 역할

$B_1$ : 찾고자 하는 모양

• $B_1$ 은 이미지 $A$ 에서 원하는 모양을 정의합니다.
• 예: $B_1$ 이 3x3 정사각형 SE 라면, $A$ 에서 이와 동일한 크기의 정사각형 모양을 찾습니다.

$B_2$ : 모양 주변 조건

• $B_2$ 는 $B_1$ 주변의 배경 조건을 설정합니다.
• $A$ 의 보수($\overline{A}$)에서 $B_2$ 와 맞는 영역을 탐지합니다.

$(A \ominus B_1) \cap (\overline{A} \ominus B_2)$ : 결합 연산

• $A$ 와 $\overline{A}$ 각각에 대해 erosion 연산을 수행한 후, 두 결과의 교집합을 구합니다.
• 이를 통해 $A$ 에서 $B_1$ 와 동일한 모양이 위치하는 픽셀을 찾습니다.

구현

b1 = np.array([[0,1,1,0],
               [1,1,1,1],
               [0,1,1,0]])
b2 = np.ones((6,6))
b2[1:5,1:5] = 1-b1

tb1 = bwerode(t, footprint=b1, mode='min')
tb2 = bwerode(1-t, footprint=b2, mode='min')
np.where((tb1 & tb2) == 1)

• b1:탐지할 모양 정의 (위 코드에서는 원형)

• b2: 배경 조건 설정 (예: b1 의 보수와 일치)

• bwerode: skimage 의 erosion 연산으로, $A$ 와 $\overline{A}$ 각각에 대해 SE 를 적용

• np.where: 두 결과의 교집합을 구하여 최종 탐지된 위치를 반환

• 결과적으로 탐지된 픽셀은 b1 과 동일한 모양을 가지며, b2 조건을 만족한다.

Morphology 활용

---

Region Filling

Region filling 은 binary image 에서 경계로 둘러싸인 내부 영역을 채우는 방법입니다. 주어진 픽셀 좌표 $p$ 가 포함된 영역 내부를 채우는 방법에 대해 알아봅시다.

알고리즘 단계

1. 초기화

• 출력 이미지 $X$ 의 초기 상태를 $X_0 = \{p\}$ 로 설정
• 반복 번호 $n = 1$ 로 시작

2. Dilation 연산

• $X_{n-1}$ 에 십자 모양의 SE 인 $B$ 를 사용하여 dilation 연산 수행: $X_n = (X_{n-1} \oplus B)$

3. 교집합 연산

• Dilation 결과와 $A$ 의 보수($\overline{A}$)의 교집합을 계산: $X_n = (X_{n-1} \oplus B) \cap \overline{A}$

4. 라벨링

• 새롭게 추가된 픽셀을 $X_n$ 에 추가

5. 수렴 조건 확인

• $X_n = X_{n-1}$ 가 될 때까지 반복
• 수렴 시 작업 종료, 그렇지 않으면 $n = n + 1$ 로 증가시키고 2단계로 돌아감

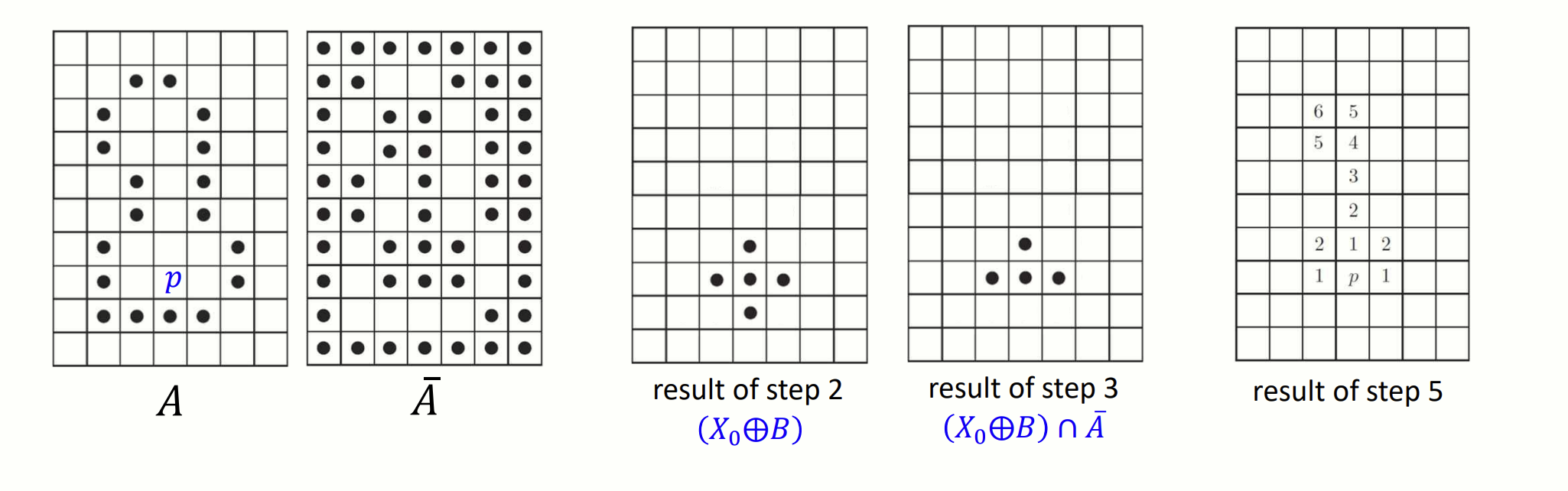
구현

from skimage.morphology import binary_erosion as bwerode
import scipy.ndimage as nd

n = io.imread('nicework.png') / 255  # 이미지 불러오기 및 이진화
B_sq = np.array([[0, 1, 0],
				 [1, 1, 1],
                 [0, 1, 0]])  # 십자 모양의 SE 생성
nb = n - bwerode(t, footprint=B_sq, mode='min')  # 내부 경계 추출
nb1 = nb[0:120, 0:80]  # 'N' 문자 영역 분리
nf = ndi.binary_fill_holes(nb1, B_sq)  # 영역 채우기
nb[0:120, 0:80] = nf  # 결과 병합

• binary_erosion: 내부 경계 추출

• binary_fill_hoels: Region filling 을 통해 경계로 둘러싸인 영역을 채움

• 결과 병합: 채워진 결과를 원래 이미지로 병합하여 최종 출력 생성

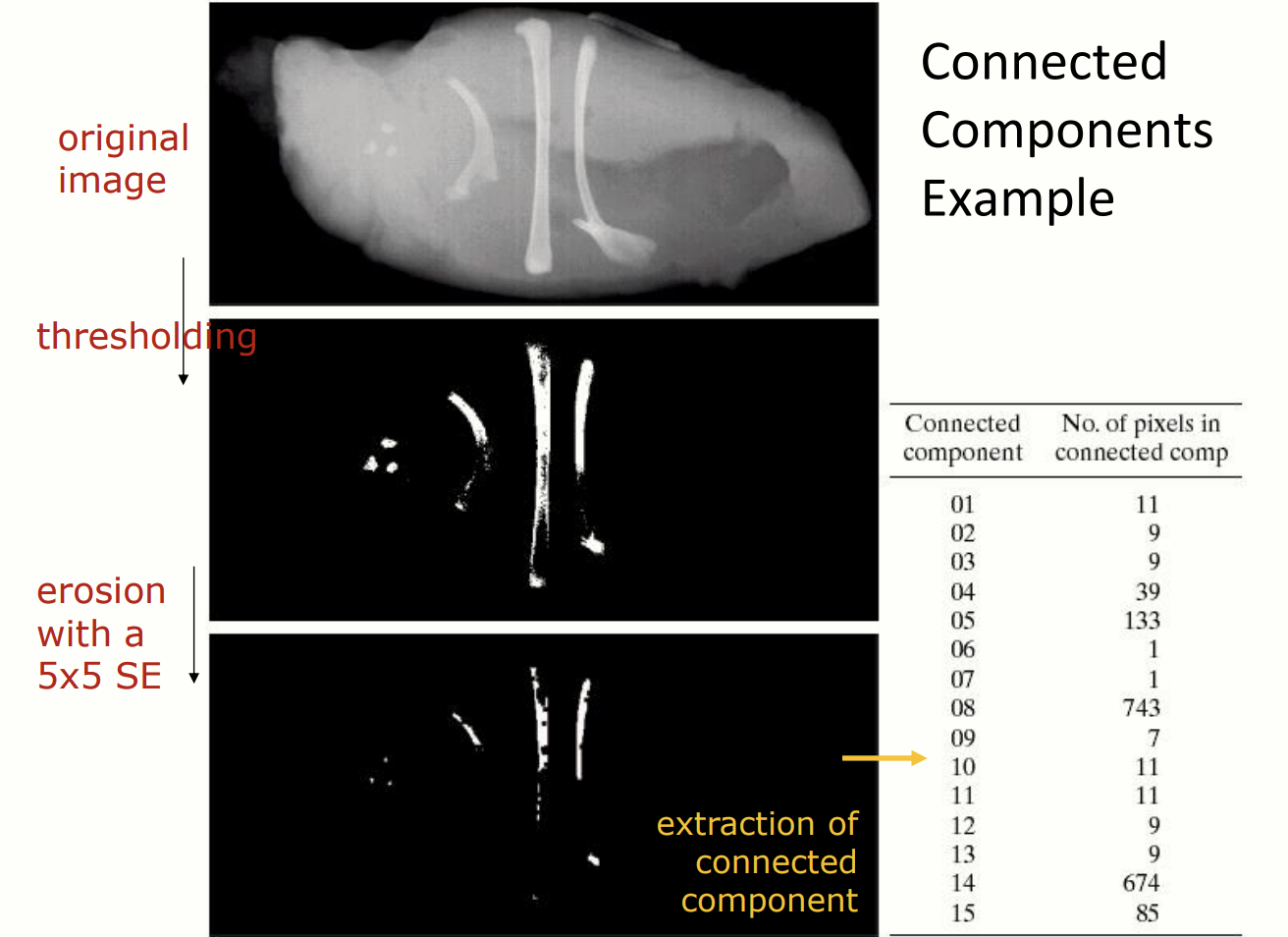
Connected Components

Connected components 는 연결된 픽셀 그룹으로, 각 그룹 내 모든 픽셀은 이웃 관계를 통해 연결되어 있습니다.

연결의 유형

1. 4-connected components: 십자 모양 SE 을 사용하여 상하좌우로 연결된 픽셀을 포함

2. 8-connected components: 정사각형 SE 을 사용하여 대각선 방향까지 포함해 연결된 픽셀을 분석

수식

• $X_0$ : 초기 픽셀 집합(시작점)
• $B$ : SE
• $\oplus$ : Dilation 연산
• $\cap$ : 입력 이미지 $A$ 와 교집합

이는 다음과 같은 알고리즘 흐름으로 진행됩니다:

1. $X_0$ 를 시작으로 dilation 을 반복 수행

2. 팽창된 결과와 $A$ 의 교집합을 계산

3. 결과가 수렴($X_n = X_{n-1}$)할 때까지 반복

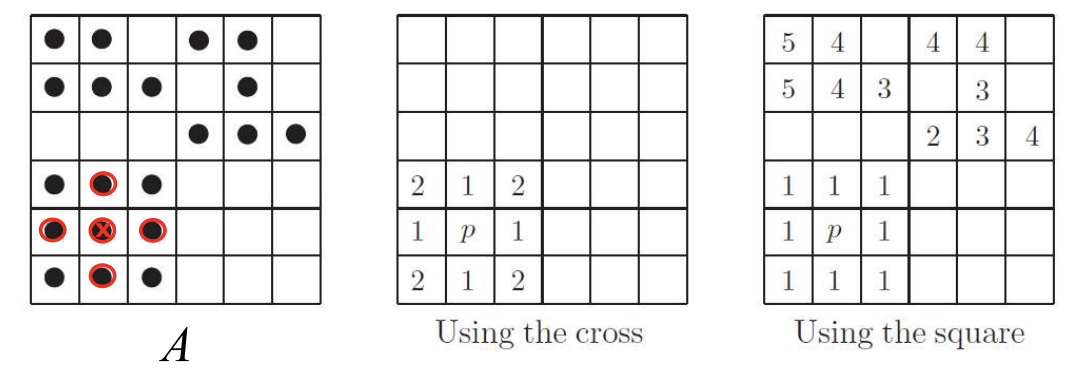
구현

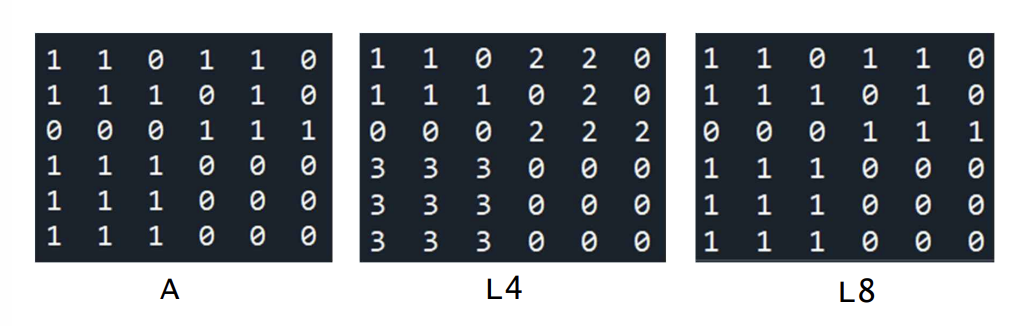
from skimage.morphology import label

# 입력 이미지 생성
A = np.zeros((6,6)).astype('uint8')
A[0,(0,1,3,4)] = 1
A[1,(0,1,2,4)] = 1
A[2,3:6] = 1
A[3:6,0:3] = 1

# 연결 성분 분석
L4 = label(A, connectivity=1)  # 4-connected components
L8 = label(A, connectivity=2)  # 8-connected components

• label 함수
  • Binary image 에서 연결된 성분을 식별
  • connectivity=1 : 4-connected
  • connectivity=2 : 8-connected
  • L4 : 4-connected-component 결과
  • L8 : 8-connected-component 결과

Skeletons

Skeleton 은 객체의 중심 축을 따라 남아있는 가장 얇은 형태의 구조를 나타냅니다. 이는 객체의 모양을 유지하면서도 최소한의 데이터로 표현하기 위해 사용됩니다.

골격 정의 방법

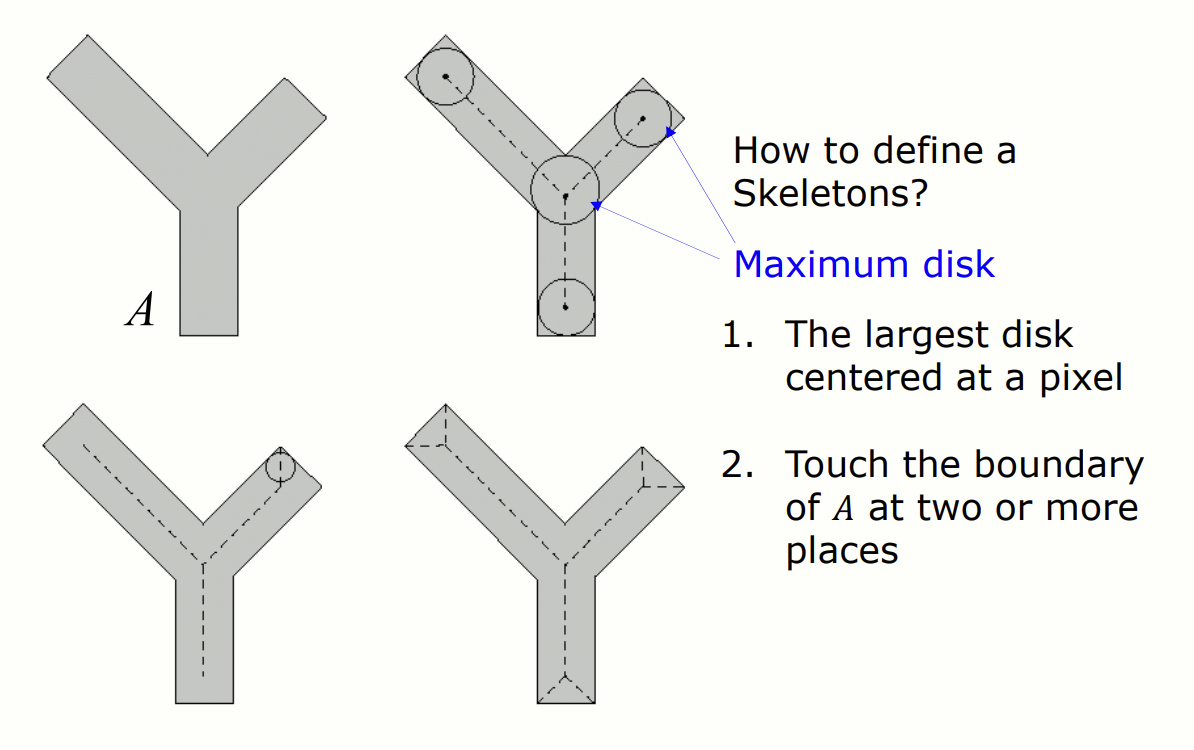
• 최대 원(Maximum Disk): 객체 내부에 있는 원 중 가장 큰 원으로 정의

1. 원의 중심이 특정 픽셀에 위치

2. 원의 가장자리(boundary)가 객체 경계(A)를 두 번 이상 접촉해야 함

계산

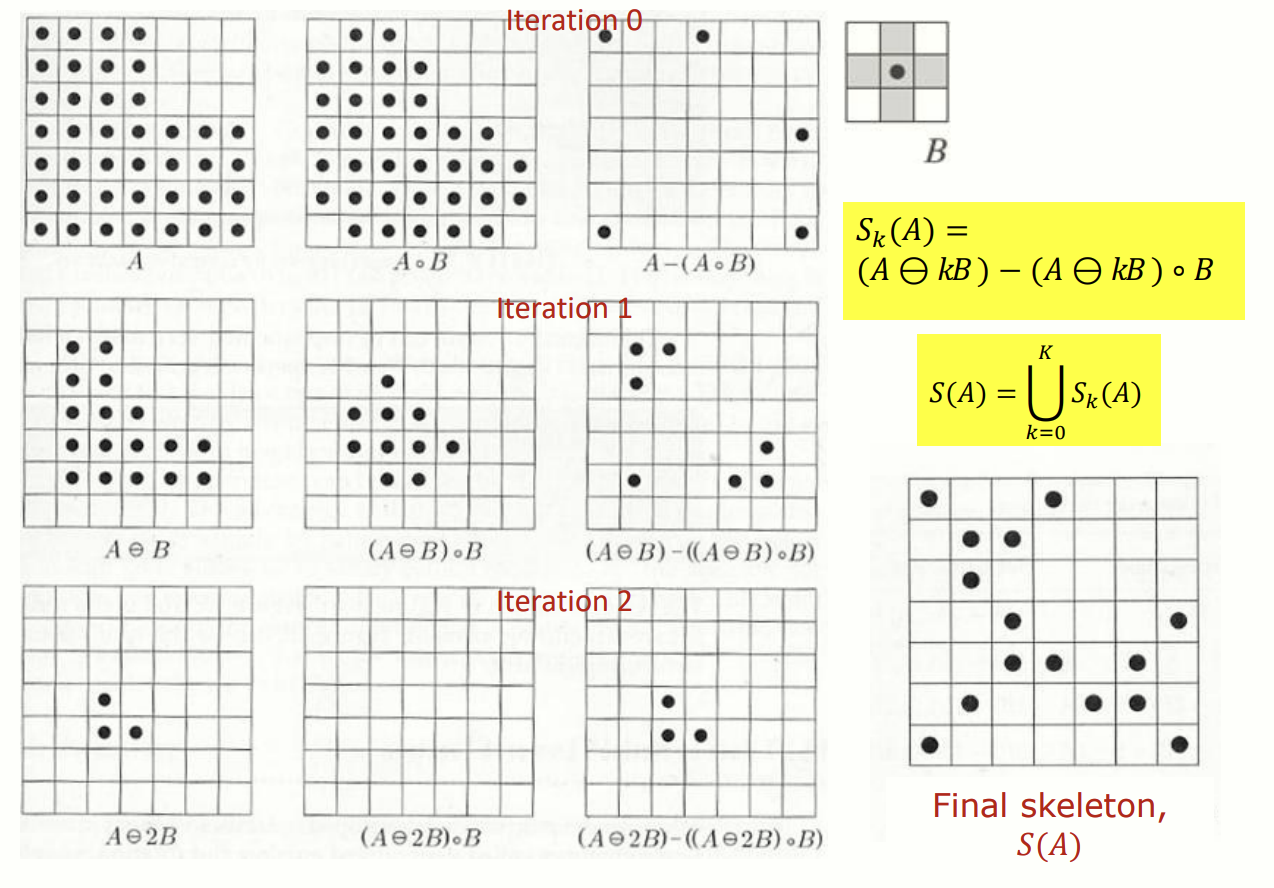
Skeleton 은 반복적인 erosion 과 opening 을 조합하여 계산합니다. 계산 과정은 다음과 같습니다:

• $A$ : 원본 이미지

• $B$ : SE

• $\ominus$ : Erosion

• $\circ$ : Opening

• $S(A) = \bigcup_{k=0}^{K} S_k(A)$ : 각 반복에서 생성된 skeleton 요소의 합집합

• $A \ominus kB$ : SE 를 사용한 $k$ 번의 erosion.

• $(A \ominus kB) \circ B$ : Erosion 된 결과를 다시 opening

• 차이 $S_k(A)$ : Erosion 결과와 opening 결과의 차집합

• $S(A)$ : 최종 skeleton 으로 모든 $S_k(A)$ 를 합친 결과

구현

from skimage.morphology import binary_erosion as bwerode
from skimage.morphology import binary_opening as bwopen

def bwskeleton(image, se):
    nr, nc = image.shape
    skeleton = np.zeros((nr, nc))  # 초기 skeleton
    eroded = image.copy()  # 이미지 복사
    
    while eroded.any():
        opened = bwopen(eroded, footprint=se)  # Opening 연산
        skeleton += (eroded - opened)  # Erosion 결과와 opening 결과 차집합
        eroded = bwerode(eroded, footprint=se)  # Erosion 연산
    
    return skeleton.astype('bool')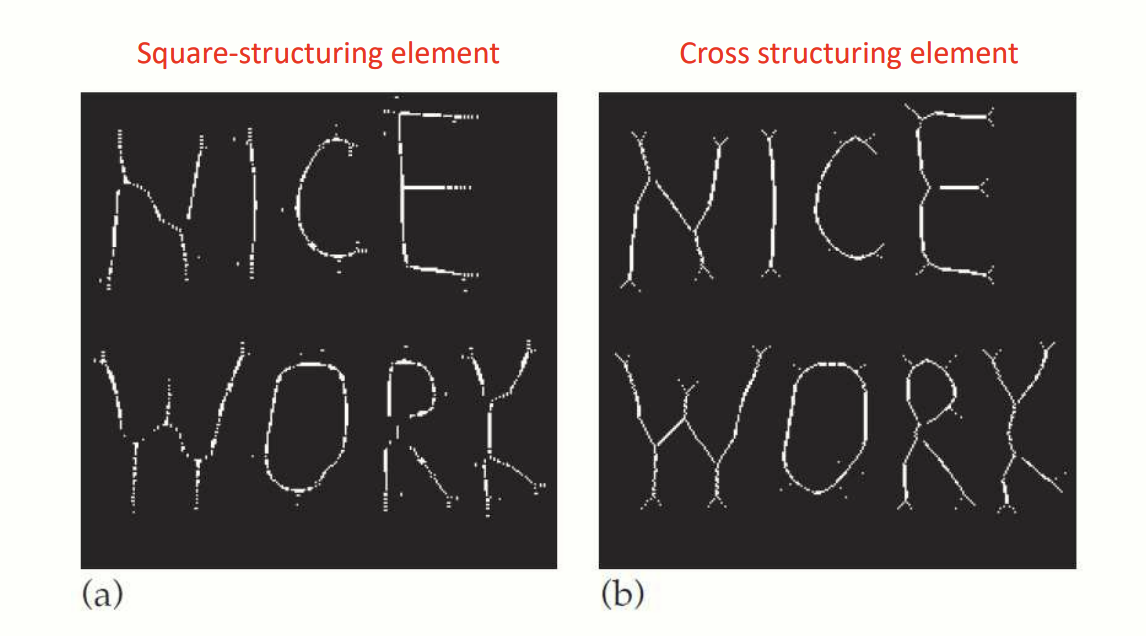

Binary image 의 skeletonization.