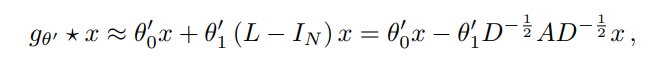[Paper]GCN

SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS
https://arxiv.org/pdf/1609.02907v4.pdf

Propagation

GCN에는 다음과 같은 propagation rule(layer-wise)이 존재한다.

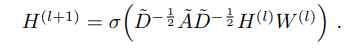
$\tilde{A}$ = $A + I_N$ : undirected graph G에 self-connection을 추가한 것
$A$ : adjacency matrix
$\sigma$ : activation function
$\tilde{D}$ : degree matrix
$W^{(l)}$ : layer-specific learnable weight matrix
$H^{(0)}$ = $X$

해당 propagation rule은 first-order approximation of localized spectral filters on graph에 의해 motivated 되었다.
https://arxiv.org/pdf/1606.09375.pdf

SPECTRAL GRAPH CONVOLUTIONS

논문에서 말하는 convolution 연산은 다음과 같은 eigen decompostion을 말한다 $\Lambda U^Tx$ : 푸리에 변환

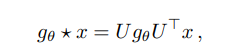
위의 propagation rule을 고려하면, $L := I_N - D^{-1/2}AD^{-1/2} = U\Lambda U^T$ 라고 표현할 수 있다.

$U$ : normalized된 Laplacian의 eigenvector들로 구성된 matrix
Laplacian matrix = Degree matrix - Adjacency matrix
$U$를 구하는 computational cost = $\mathcal{O}(N^2)$
$\Lambda$의 cost도 비싸기 때문에 아래와 같은 근사법이 제시됨.

[-1,1] 범위의 Orthogonal basis인 K번째 chebyshev polnomial $T_k$까지만 고려해서 근사한다.

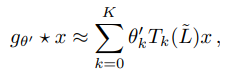
$\int_{-1}^{1} T_n(x)T_m(x) {dx \over \sqrt{1-x^2}}$ = 0 (n != m)
$\theta_k$ : k번째 basis 방향으로 내적 coefficient

예를들어, $\lambda_{max} = 2$ & $k = 1 인 경우는 다음과 같다.$

$T_0 = 1$
$T_1 = x$