앞서 본 BST 와 Red-Black Tree는 이진트리다.
이번에 볼 B-Tree는 다중 분류 트리로, Depth를 줄일 수 있다.
📕 B-tree
- B-tree는 언제 사용할까?
메모리 접근에서 이 B트리를 사용한다. 메모리 접근시, 하나의 Depth를 내려가는 데에 디스크 블록을 새롭게 찾아야 하기 때문에 Disk Access 시간이 많이 소요된다. 여기서 '블록(페이지)'은 디스크의 접근 단위이다.
" 디스크로부터 데이터를 읽거나 기록할 때 이를 포함하는 디스크 블록 전체를 메모리로 읽어오고 다시 블록 전체를 디스크에 기록하는 방식으로 디스크 I/O "
디스크에 한 번 접근하는 시간은 수십만 명령어의 처리 시간과 맞먹는다고 한다. 이때 검색트리가 디스크에 저장되어 있다면 트리의 높이(또는 깊이, Depth)를 최소화 하는 것이 유리하다. 트리에서 같은 level에서 key를 찾는 시간보다 Depth를 내려가는 데에 시간이 더 많이 소요되기 때문이다.
-
다진 검색트리란?
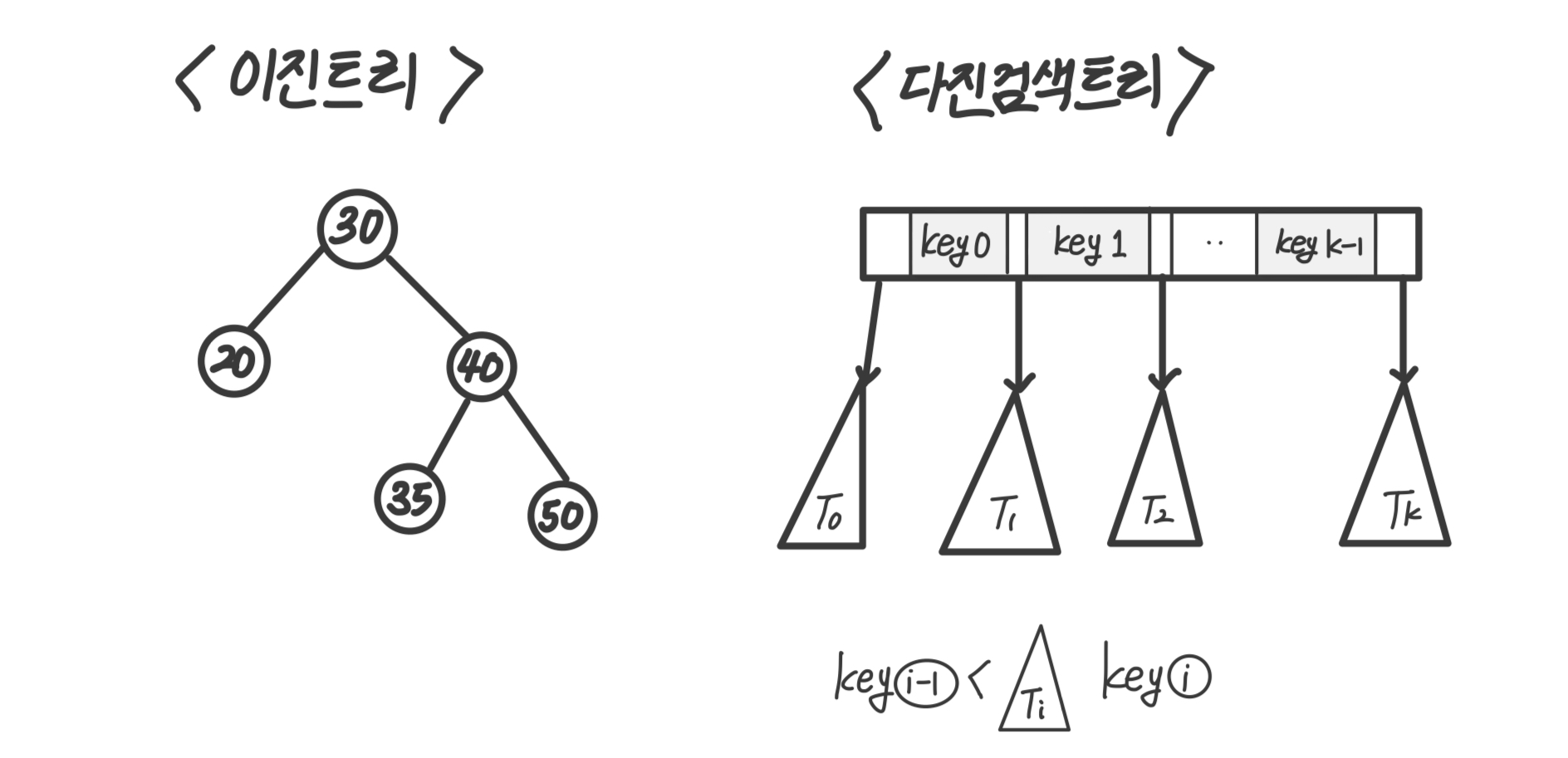
오른쪽, 왼쪽 자식 2가지로 뻗어나가는 이진트리와 다르게 여러 갈래로 나뉘는 트리를 다진검색트리라고 한다. key를 기준으로 뻗어나간다.
-
B-Tree
B트리는 균형잡힌(Balanced Tree) 다진검색트리다. 그래서 최악의 경우인 한 쪽으로만 노드가 늘어진 경우를 보완하여 디스크 접근 횟수를 줄일 수 있다. -
B-Tree의 성질
B트리는 다음 성질을 만족한다.1. 루트를 제외한 모든 노드는 ~ 개의 키를 가진다.
2. 모든 리프노드는 같은 깊이를 가진다(Balanced)1번 특성 예시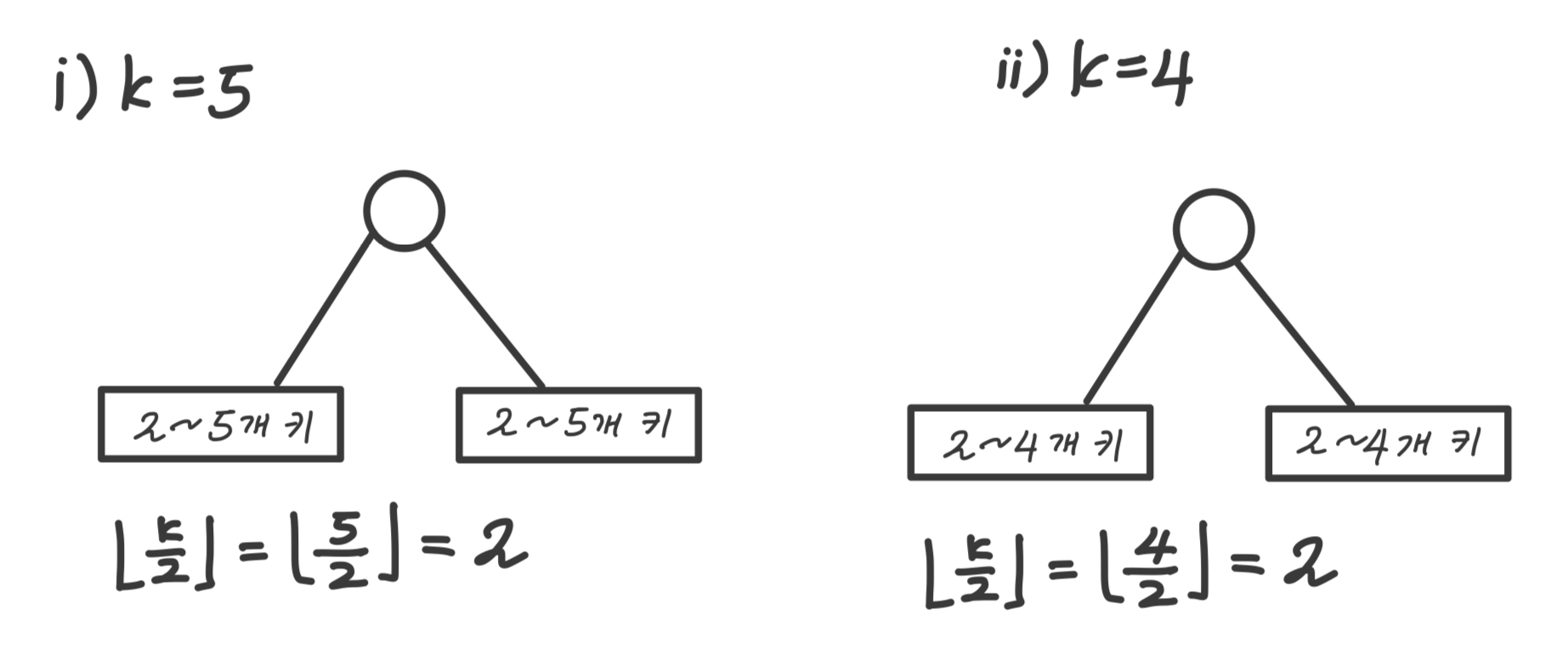
📗 B-Tree에서의 삽입
B-Tree에서의 삽입을 수도코드와 그림으로 알아보자.
삽입하는 함수 BTreeInsert는 트리의 루트노드인 t와 삽입하고자 하는 키 x를 파라미터로 받는다.
BTreeInsert(t, x)
{
x를 삽입할 리프노드 r을 찾는다;
x를 r에 삽입한다;
if (r에 오버플로우 발생) then clearOverflow(r);
}- k=4라고 할 때, 한 노드에서는 2~4개의 키를 가질 수 있다. 이때 key가 하나 더 들어와서 오버플로우가 발생한 경우, 처리를 해줘야 한다.

오버플로우가 발생할 때 처리하는 함수는 clearOverflow(r) 이다.
clearOverflow(r)
{
if (r의 형제노드 중 여유가 있는 노드가 있음) then {r의 남는 키를 넘긴다};
else {
r을 둘로 분할하고 가운데 키를 부모노드로 넘긴다;
if (부모노드 p에 오버플로우 발생) then clearOverflow(p);
}
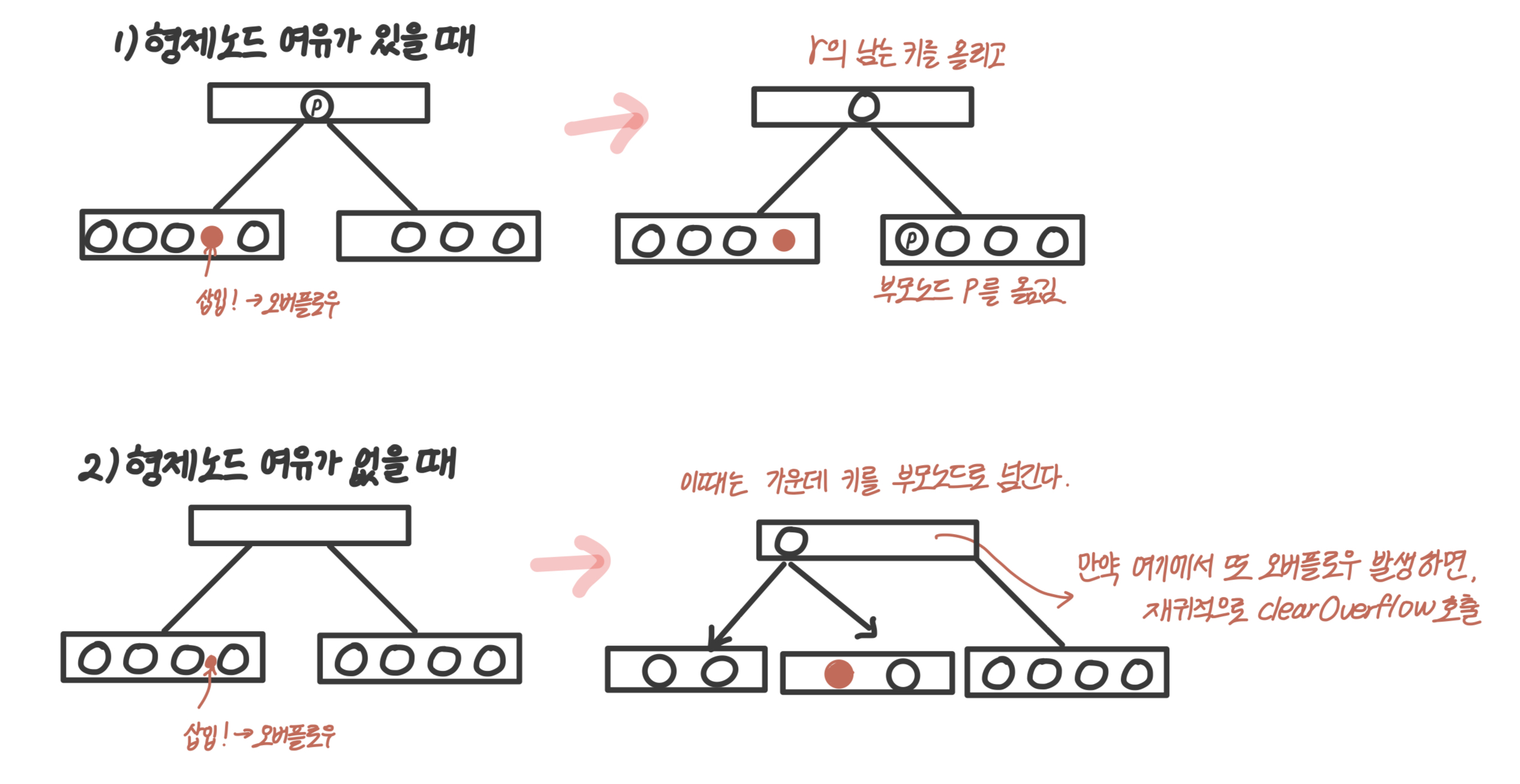
}- 오버플로우가 발생하는 경우 두 경우로 나눠서 처리한다. 자세한 방법은 아래 그림에서 확인할 수 있다.
- 형제노드에 여유가 있을 때 : 형제노드로 옮긴다.
- 형제노드에 여유가 없을 때 : 가운데 키를 부모노드로 넘기고 노드를 분리한다. (부모노드에서도 오버플로우가 발생하면 재귀적으로 clearOverflow 호출)
📘 B-Tree의 삭제연산
삭제연산을 수행하는 BTreeDelete는 트리의 루트노드 t와 삭제하고자 하는 키 x, 그리고 x를 갖고 있는 노드 v를 파라미터로 받는다.
BTreeDelete(t, x, v)
{
if(v가 리프노드가 아님) then {
x의 직후원소 y를 가진 리프노드를 찾는다;
x와 y를 맞바꾼다;
}
리프노드에서 x를 제거하고 이 리프노드를 r이라고 한다;
if(r에서 언더플로우 발생) then clearUnderflow(r);
}- 그림으로도 삭제연산을 살펴보자.
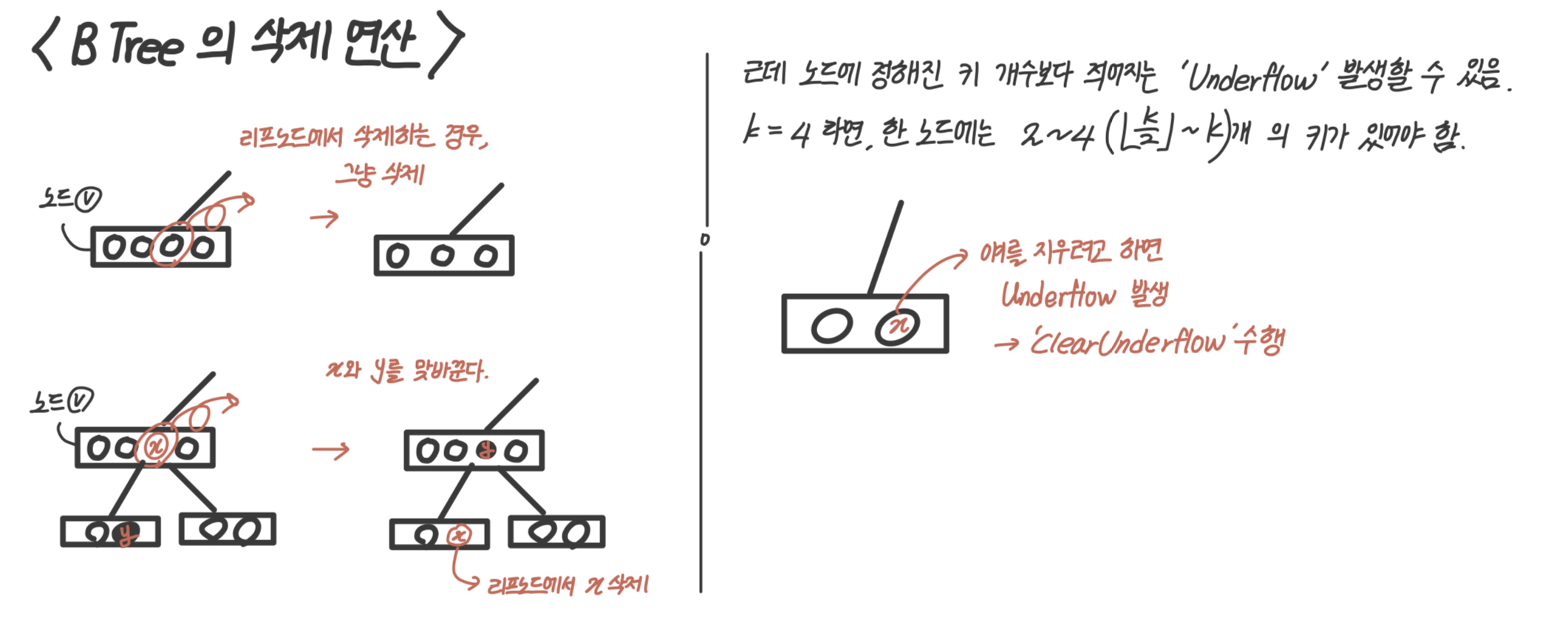
근데 이때 key의 개수가 적어지는 'Underflow' 가 발생할 수 있다. 이때 clearUnderflow 함수를 호출한다.
clearUnderflow(r)
{
if(r의 형제노드 중 키를 하나 내놓을 수 있는 여분을 가진 노드가 있음)
then {r이 키를 넘겨받는다;}
else{
r의 형제노드와 r을 합병한다;
if(부모노드 p에 언더플로우 발생) then clearUnderflow(p);
}
}-
경우1) r의 형제노드 중 키를 하나 내놓을 수 있는 여분을 가진 노드가 있는 경우
- 아래처럼 회전하듯 처리해준다.
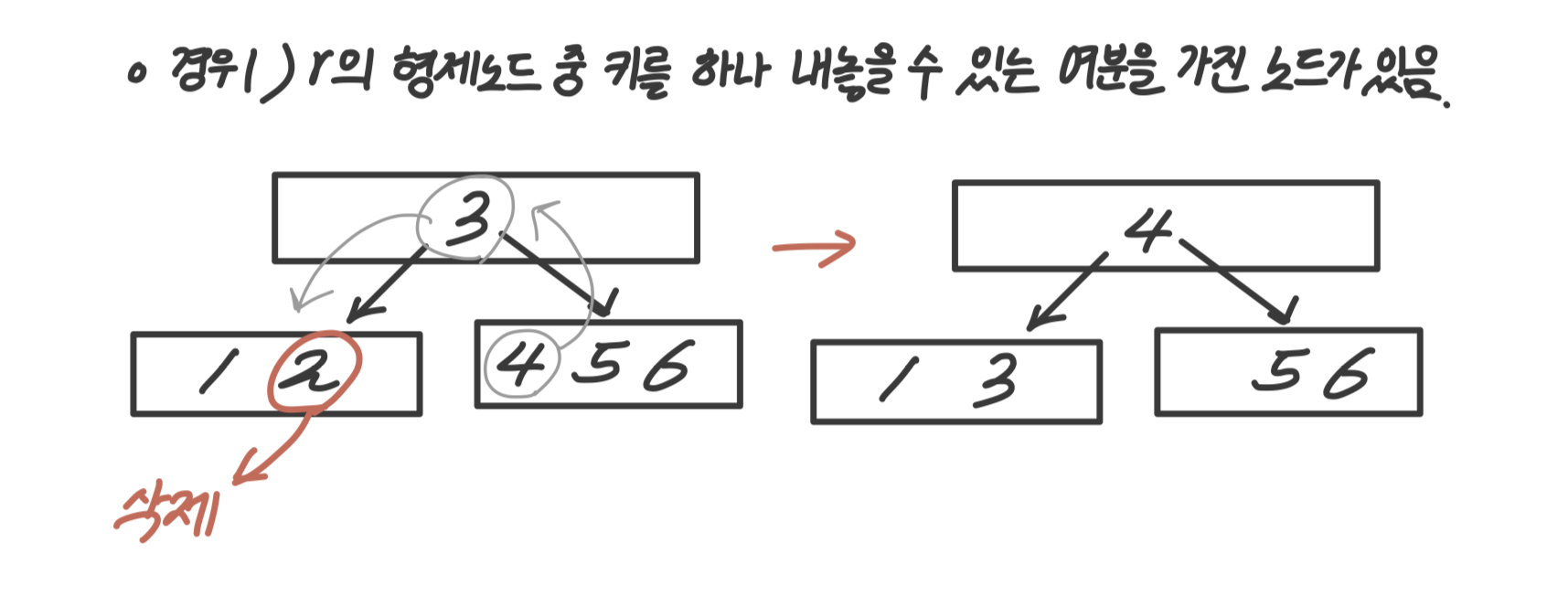
- 아래처럼 회전하듯 처리해준다.
-
경우2) 형제노드 중 키를 넘겨받을 수 없을 때
- 형제노드와 합병한다. 이때 부모노드 p와 함꼐 병합한다. 부모노드를 가져왔기 때문에 위에서 또 언더플로우가 발생할 수 있고, 이러면 재귀적으로 다시 처리한다.
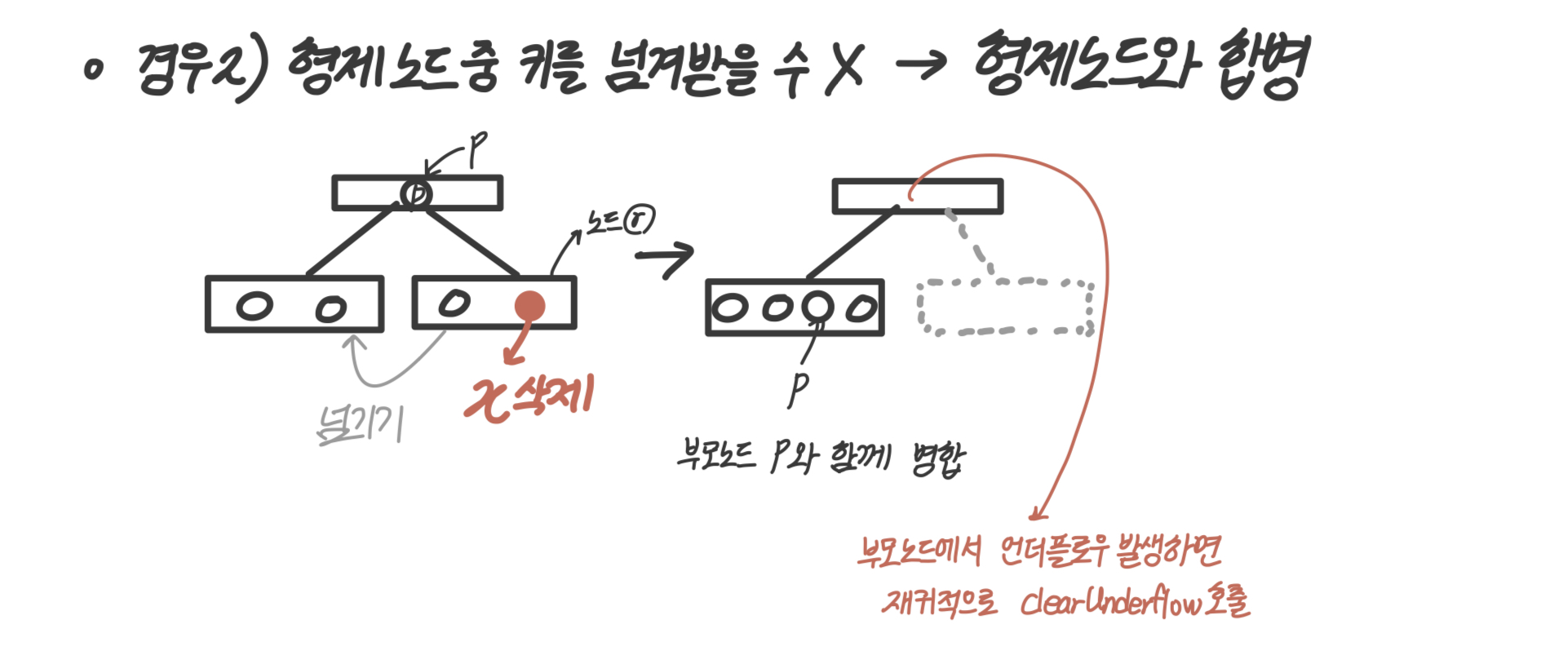
- 형제노드와 합병한다. 이때 부모노드 p와 함꼐 병합한다. 부모노드를 가져왔기 때문에 위에서 또 언더플로우가 발생할 수 있고, 이러면 재귀적으로 다시 처리한다.
