각 문제는 (1) 재귀적 해법, (2) DP의 Top-Down(memoization)형식, (3) Bottom-up(tabulation) 세 가지 형식으로 문제를 푼다. 모두 파이썬을 사용한다.
1️⃣ 조약돌 문제
1) 재귀적 해법
# 1. weight 계산하기
import copy
A = [[6,-8,11], [7,10,12],[12,14,7],[-5, 9, 4],[5, 7, 8],[3, 13, -2],[11, 8, 9],[3, 5, 4]]
A2 = [[6,-8,11], [7,10,12],[12,14,7],[-5, 9, 4],[5, 7, 8],[3, 13, -2],[11, 8, 9],[3, 5, 4],
[6,-8,11], [7,10,12],[12,14,7],[-5, 9, 4],[5, 7, 8],[3, 13, -2],[11, 8, 9],[3, 5, 4]]
def append_weight(A):
# w = A
# w = A.copy()
w = copy.deepcopy(A)
for i in range(len(w)):
w[i].append(w[i][0] + w[i][2])
return w
w = append_weight(A)def pebbleSum():
n = len(w)
m = [pebble(n-1,0), pebble(n-1,1), pebble(n-1,2), pebble(n-1,3)]
return max(m)
def pebble(i, p):
"""i 번째 열에서 패턴 p(0,1,2,3)번을 선택하는 경우"""
if i == 0:
return w[0][p]
else:
M = -100
for q in range(4):
if compatible(p, q) == True:
tmp = pebble(i-1, q)
if tmp > M:
M = tmp
return M + w[i][p]
def compatible(p,q):
if (p == 3 and q == 0) or (p == 3 and q == 2) or (p==q):
return False
return True
start_time = time.time()
w = append_weight(A)
print(pebbleSum())
print("\n %.4f sec." % (time.time() - start_time))2) DP : Bottom-Up(Tabulation) 방식
def pebbleSum_DP_bottomup(w):
cache = [[None for j in range(4)] for i in range(len(A))]
for i in range(len(A)):
if i == 0:
cache[0] = w[0]
else:
cache[i][3] = cache[i-1][1] + w[i][3]
for p in range(3):
cache[i][p] = max([cache[i-1][x] for x in range(4) if x != p]) + w[i][p]
return max([cache[-1][x] for x in range(4)])
start_time = time.time()
w = append_weight(A)
# w = append_weight(A2)
print(pebbleSum_DP_bottomup(w))
print("\n %.4f sec." % (time.time() - start_time))3) DP : Top-Down(Memoization) 방식
def pebble_memo(w, i, p, cache):
if i == 0:
cache[0] = w[0]
if cache[i][p] != None:
return cache[i][p]
else:
if p == 3:
M = pebble_memo(w, i-1, 1, cache)
else:
M = max([pebble_memo(w, i-1, j, cache) for j in range(4) if j != p])
cache[i][p] = M + w[i][p]
return M + w[i][p]
def pebbleSum_DP_topdown():
cache = [[None for j in range(4)] for i in range(len(A))]
n = len(w)
m = [pebble_memo(w, n-1, i, cache) for i in range(4)]
return max(m)
start_time = time.time()
w = append_weight(A)
# w = append_weight(A2)
print(pebbleSum_DP_topdown())
print("\n %.4f sec." % (time.time() - start_time))2️⃣ 최소 행렬경로 문제
1) 재귀적 해법
# 예시로 사용
m1 = [[6,7,12,5], [5,3,11,18], [7,17,3,3], [8,10,14,9]]
m2 = [[6,7], [5,3], [7,17]]
m3 = [[6,7,12,5], [5,3,11,18], [7,17,3,3], [8,10,14,9],
[6,7,12,5], [5,3,11,18], [7,17,3,3], [8,10,14,9]]def matrixPath(i, j):
if (i==0)&(j==0): return m[0][0]
elif i == 0: return matrixPath(0, j-1) + m[i][j]
elif j == 0: return matrixPath(i-1, 0) + m[i][j]
else: return min(matrixPath(i-1, j), matrixPath(i, j-1)) + m[i][j]
m = m3 # m1, m2, m3로 바꿔가면서 테스트해볼 수 있음
matrixPath(3,3)2) DP : Bottom-Up(Tabulation) 방식
def matrixPath_DP_BU(i, j):
n1 = len(m)
n2 = len(m[0])
c = copy.deepcopy(m)
for i in range(1, n1):
c[i][0] = m[i][0] + c[i-1][0]
for j in range(1, n2):
c[0][j] = m[0][j] + c[0][j-1]
for i in range(1, n1):
for j in range(1, n2):
c[i][j] = m[i][j] + min(c[i-1][j], c[i][j-1])
return c[n1-1][n2-1]
m = m1
print(len(m)-1, len(m[0])-1)
matrixPath_DP_BU(len(m)-1, len(m[0])-1)3) DP : Top-Down(Memoization) 방식
import copy
m1 = [[6,7,12,5], [5,3,11,18], [7,17,3,3], [8,10,14,9]] # 교재의 예제
m2 = [[6,7], [5,3], [7,17]]
m3 = [[6,7,12,5], [5,3,11,18], [7,17,3,3], [8,10,14,9],
[6,7,12,5], [5,3,11,18], [7,17,3,3], [8,10,14,9]]
m = m1 # m1, m2, m3로 바꿔가면서 테스트해볼 수 있음
n1 = len(m)
n2 = len(m[0])
c = [[None]*n2 for x in range(n1)]
def matrixPath_DP_TD(i,j):
# Top-Down 방식의 DP로 구현하시오.
# (0,0)인 경우,
if (i==0)&(j==0):
c[0][0] = m[0][0]
return c[0][0]
# 0행인 경우,
if (i==0)&(j!=0):
c[i][j] = matrixPath_DP_TD(0, j-1) + m[i][j]
return c[i][j]
# 0열인 경우,
if (i!=0)&(j==0):
c[i][j] = matrixPath_DP_TD(i-1, 0) + m[i][j]
return c[i][j]
# 이미 계산한 적 있으면 반환
if c[i][j] != None:
return c[i][j]
# 계산한 적 없는 경우,
c[i][j] = min(matrixPath_DP_TD(i-1, j), matrixPath_DP_TD(i, j-1)) + m[i][j]
return c[i][j]
print(len(m)-1, len(m[0])-1)
matrixPath_DP_TD(len(m)-1, len(m[0])-1)3️⃣ 연쇄행렬 최소곱셈 순서 문제
행렬에서 곱셈연산의 수는 행렬의 크기의 곱으로 나타낼 수 있다.
예를 들어 A(2x3), B(3x4)크기의 행렬끼리의 곱인 AxB을 하면, 2x3x4번의 곱셈이 필요하다.
문제는 세 개 이상의 행렬의 곱에서는 어떤 행렬끼리의 곱을 먼저 수행하느냐에 따라 곱셈 연산 수가 많이 달라진다는 것이다.
예를 들어 아래 행렬을 보자. 괄호 안은 행렬의 크기를 의미한다.
A행렬 : (10x100)
B행렬 : (100x5)
C행렬 : (5x50)
- (AB)C 로 수행하는 경우
- AB 행렬곱에는 10x100x5 번의 곱셈 필요 -> 10x5 행렬 생성
- 총 10x100x5 + 10x5x50 = 7500 번의 곱셈 필요
- A(BC) 로 수행하는 경우
- BC 행렬곱에는 100x5x50 번의 곱셈 필요 -> 100x50 행렬 생성
- 총 100x5x50 + 10x100x50 = 75000 번의 곱셈 필요
- 따라서 이 경우에는 (AB)C로 계산하는 게 효율적이다. 이렇듯, 행렬의 곱의 순서에 따라 효율성이 달라지니, 어떻게 계산하는 게 더 좋은지 알아볼 필요가 있다.
풀이
행렬이 A, B, C, D 로 4개가 있을 땐, 총 번의 경우의 수를 살펴봐야 한다.
1) ((AB)C)D
2) A(B(CD))
3) (AB)(CD)
4) (A(BC)D)
n개의 행렬이 있을 때는 몇 번의 경우의 수를 살펴봐야할까?
-
아래처럼 n개의 행렬이 있을 때 마지막으로 행렬곱이 수행되는 상황에서는 n-1개의 경우의 수가 나온다.
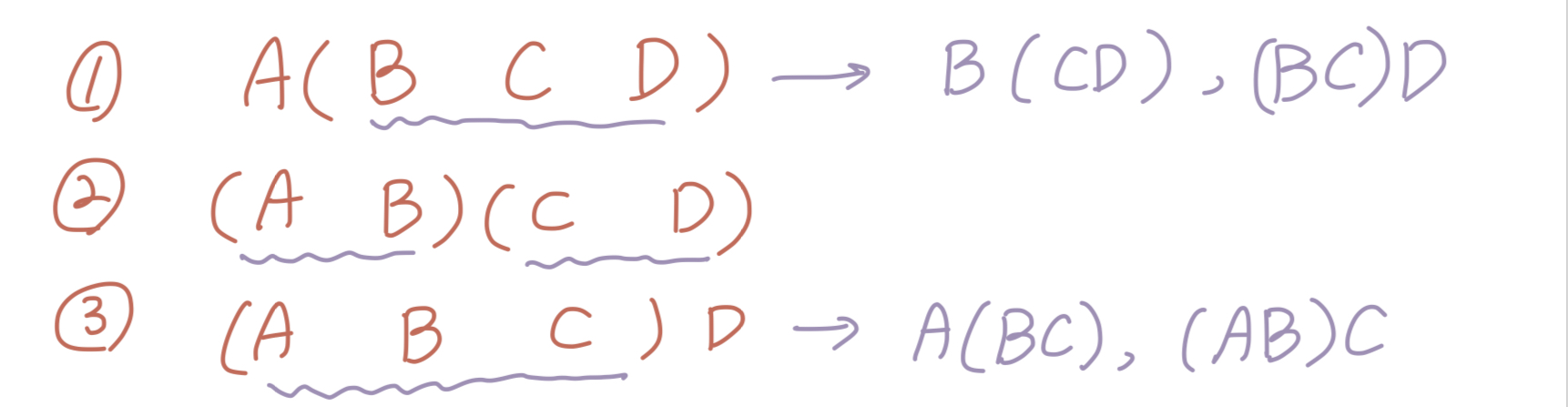
-
두 개씩 묶인 2번과 달리 1번과 3번은 또 괄호 안의 경우에 대해 최소로 곱셈연산이 수행되는 것을 찾아야 한다.
-
이렇게 작은 문제로 나누어서 풀 수 있기 때문에 Divide and Conquer로 풀 수 있다. 분할 정복 알고리즘은 보통 재귀 함수(recursive function)를 통해 자연스럽게 구현된다.
- 분할 정복에 대한 내용은 여기에서 확인 가능
-
재귀적 관계를 알아보자
의 행렬곱의 최소 곱셈 연산을 구하는 경우,
는 에서의 최소 곱셈 연산이고
의 차원을 라고 할 때, 아래처럼 재귀관계를 작성할 수 있다.
1) 재귀적 해법
위 식을 이해했다면 이를 Divide and Conquer 방식인 재귀로 풀어보자.
# 예시로 사용
p1 = [10, 100, 5, 50] # 10x100, 100x5, 5x50 행렬을 곱하는 경우를 의미
p2 = [10, 100, 5] # 10x100, 100x5 행렬을 곱하는 경우를 의미
p3 = [10, 100, 5, 50, 10, 100, 5, 50, 10, 100, 5, 50, 10, 100, 5, 50]import math
def rMatrixChain(i, j):
if i == j:
return 0
minimum = math.inf
for k in range(i, j):
q = rMatrixChain(i, k) + rMatrixChain(k+1, j) + p[i-1]*p[k]*p[j]
if q < minimum:
minimum = q
return minimum
import time # 각 방식의 시간을 체크하기 위함
start_time = time.time()
p = p3 # p1, p2, p3로 바꿔가며 테스트
print(rMatrixChain(1, len(p)-1))
print("%.5f sec" %(time.time()-start_time))2) DP : Bottom-Up(Tabulation) 방식
- 테이블은 아래처럼 채워나가면 된다.
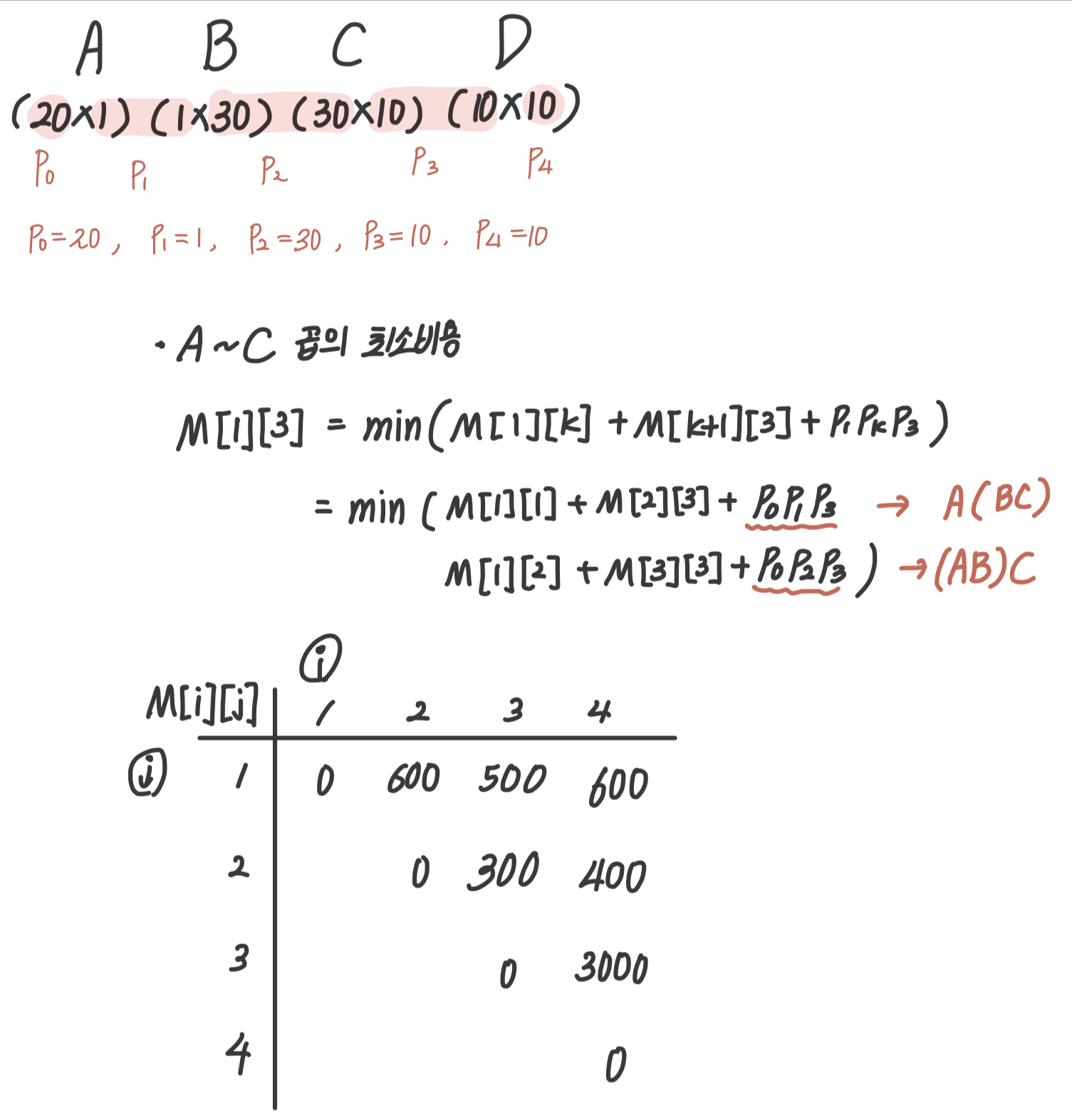
def matrixChain_DP_BU():
n = len(p) - 1 # 행렬 개수
M = [[0]*n for x in range(n)]
for r in range(1, n):
for i in range(0, n-r):
j = i+r
M[i][j] = min([M[i][k] + M[k+1][j] + p[i-1]*p[k]*p[j] for k in range(i, j)])
return M[0][-1]
p = p2
matrixChain_DP_BU()3) DP : Top-Down(Memoization) 방식
import time
p = p3
n = len(p)-1 # n: 행렬 개수
m = [[None]*(n) for x in range(n)] # m[i][j]는 Ai~Aj를 곱하는 최소 비용
def matrixChain_DP_TD(i, j):
if i==j:
m[i][j] = 0
# 이미 계산한 적 있으면 반환
if m[i][j] != None:
return m[i][j]
# 계산한 적 없는 경우,
m[i][j] = min(matrixChain_DP_TD(i,k) + matrixChain_DP_TD(k+1,j) + p[i-1]*p[k]*p[j]for k in range(i, j))
return m[i][j]
start_time = time.time()
print(matrixChain_DP_TD(0, n-1))
print("\n %.5f sec." % (time.time() - start_time)) # 재귀적 호출에 비하여 시간이 1/1000 수준으로 단축됨4️⃣ LCS(Longest Common Subsequence) 문제
두 문자열에 공통적으로 들어있는 common subsequence중 가장 긴 것의 길이를 구하는 문제이다.
input
X = "abcbdab", Y = "bdcaba"
output
4
설명
"abcbdab"와 "bdcaba"에서 "bcba"가 공통적으로 최장 공통부분이 되어 결과값은 이 공통부분의 길이인 4이다.
1) 재귀적 해법
X = "abcbdab"
Y = "bdcaba"
def rLCS(m,n): # m과 n은 비교할 개수
if (m==0)|(n==0):
return 0
elif X[m-1] == Y[n-1]:
return rLCS(m-1, n-1) + 1
return max(rLCS(m-1,n), rLCS(m,n-1))
rLCS(len(X), len(Y))2) DP : Bottom-Up(Tabulation) 방식
def LCS_DP_BU(m,n): # m과 n은 비교할 개수
C = [[0]*(n+1) for x in range(m+1)]
for i in range(1, m+1):
for j in range(1, n+1):
if X[i-1] == Y[j-1]:
C[i][j] = C[i-1][j-1] + 1
else:
C[i][j] = max(C[i-1][j], C[i][j-1])
return C[m][n]
X = "abcbdab"
Y = "bdcaba"
LCS_DP_BU(len(X), len(Y))C는 아래와 같은 Table이 나옴
[[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 1, 1],
[0, 1, 1, 1, 1, 2, 2],
[0, 1, 1, 2, 2, 2, 2],
[0, 1, 1, 2, 2, 3, 3],
[0, 1, 2, 2, 2, 3, 3],
[0, 1, 2, 2, 3, 3, 4],
[0, 1, 2, 2, 3, 4, 4]]3) DP : Top-Down(Memoization) 방식
X = "abcbdab"
Y = "bdcaba"
# Top-Down 방식의 DP로 구현하시오.
m = len(X) #7
n = len(Y) #6
C = [[None]*(n+1) for x in range(m+1)]
def LCS2_DP_TD(i,j): # m과 n은 비교할 개수
if i == 0 or j == 0:
return 0
# 이미 계산한 적 있으면 반환
if C[i][j] != None:
return C[i][j]
if X[i-1] == Y[j-1]:
C[i][j] = LCS2_DP_TD(i-1, j-1) + 1
return C[i][j]
# 같지 않으면
C[i][j] = max(LCS2_DP_TD(i-1, j), LCS2_DP_TD(i, j-1))
return C[i][j]
LCS2_DP_TD(len(X), len(Y))
