학교 수업인 산업경영알고리즘 중간고사를 대비하기 위한 기록입니다.
BST에 대한 자세한 설명은 여기에서 확인할 수 있습니다.
(추후 코드 구현해서 추가할 예정입니다.)
📕 불균형 이진트리의 문제점
기존 Binary Search Tree는 노드가 한 쪽으로 치우치는 경우, 즉 불균형 이진 트리(Unbalanced Binary Tree)가 될 수 있다.
이게 왜 문제일까?
-
BST의 시간복잡도는 아래와 같다. 여기에서 worst case가 바로 불균형일 때 발생한다.
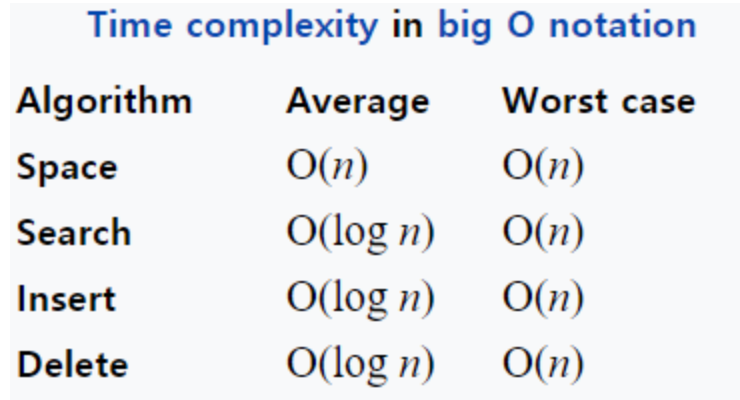
-
BST 장점이 데이터 탐색할 때 절반씩 날리면서 찾을 수 있다는 건데 아래처럼 되어 있으면 그 쓸모가 없을 거다.
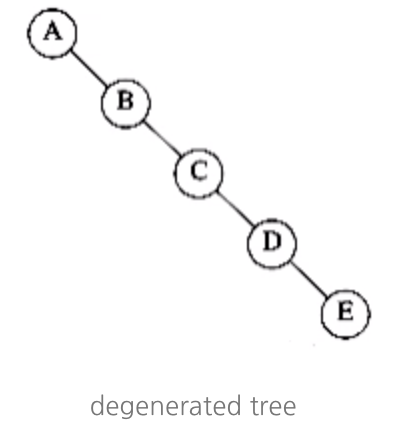
BST의 효율을 높이기 위해서는 Unbalanced Binary Tree를 Balanced Binary Tree로 바꿔주어야 한다. Red-Black Tree는 이 문제를 해결해준다.
📗 Red-Black Tree란?
줄여서 RB Tree는 데이터가 추가될 때마다 Balancing을 해주어 깊이를 맞춰준다.
'Red-Black'이라는 이름대로 모든 노드에 블랙 또는 레드 색을 칠한다.
그리고 아래의 '레드블랙 특성'을 만족해야 한다.
레드블랙 특성
1. 루트는 블랙이다. (시작 블랙)
2. 모든 리프는 블랙이다. (끝도 블랙)
3. 어떤 노드가 레드이면 그 노드의 자식은 반드시 블랙이다. (레드 다음엔 꼭 블랙, 반대로 블랙의 자식은 꼭 레드일 필요는 없음)
4. 루트 노드에서 임의의 리프 노드에 이르는 경로에서 만나는 블랙 노드의 수는 모두 같다.
아래 레드블랙트리를 보자.
1. 루트노드는 블랙이다.
2. leaf 노드를 모두 NIL(None)으로 뒀고, 모두 블랙이다.
3. 레드 다음에 블랙이 온다.
4. 어떤 리프노드로 가든, 그 경로에 3개의 블랙 노드가 있다.
-
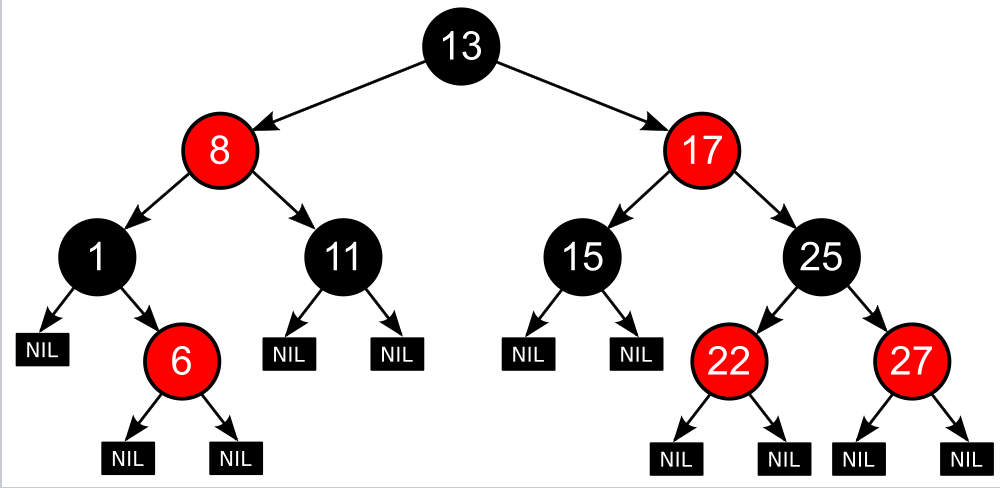
-
실제 구현시에는 아래처럼 NIL을 처리한다.
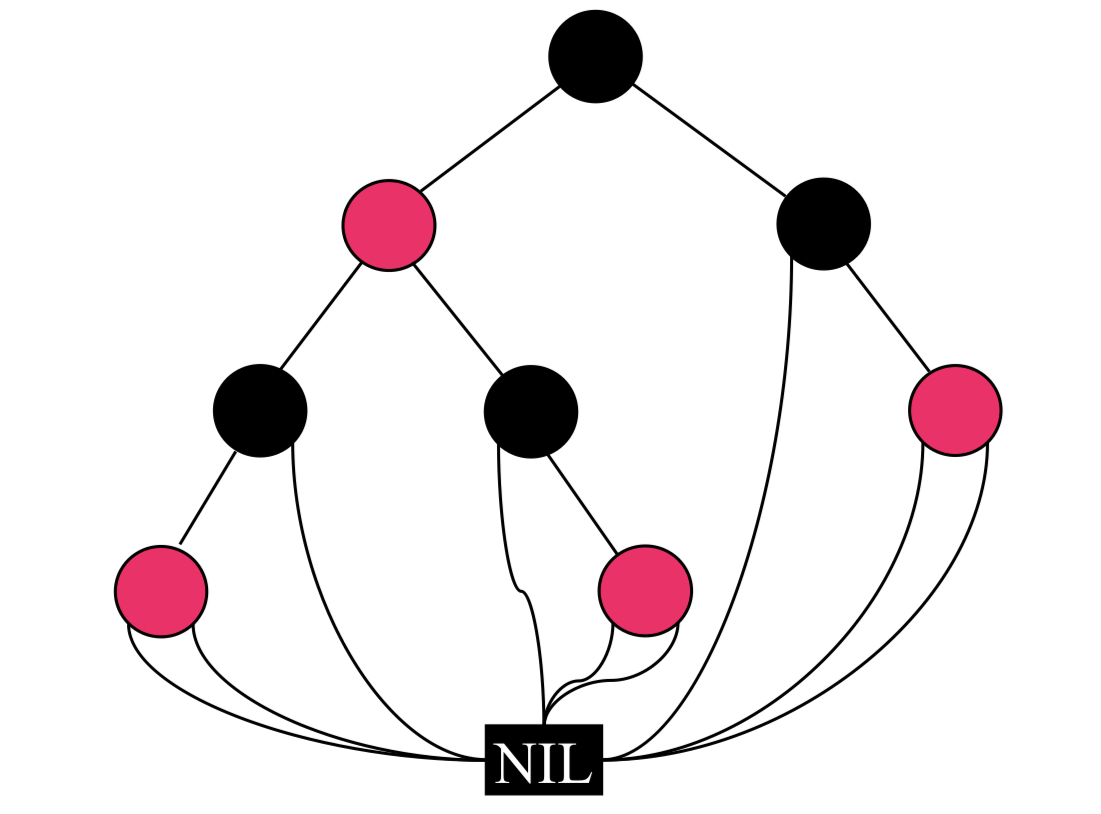
그럼 이제 RB tree에서의 삽입연산과 삭제연산을 살펴보자. 탐색은 기존 BST와 동일하다!
📘 RB tree의 삽입연산
위에서 말했듯 RBtree에선 새로운 데이터가 들어올 때마다 리밸런싱을 해줘야 하기 때문에 원래 BST와는 다르게 좀 복잡한 삽입연산을 한다.
- 우선 새로 넣을 노드(x)는 '레드'로 칠한다. 아래 예시 그림에서는 분홍색으로 표시했다.
BST에서 하는 것처럼 삽입을 진행한다. 이때 왼쪽처럼 부모노드(p)가 블랙이면 아무 문제가 없다. 반면 오른쪽처럼 새로 넣은 노드의 부모가 레드면 '레드블랙 특성 3번'이 깨진다.
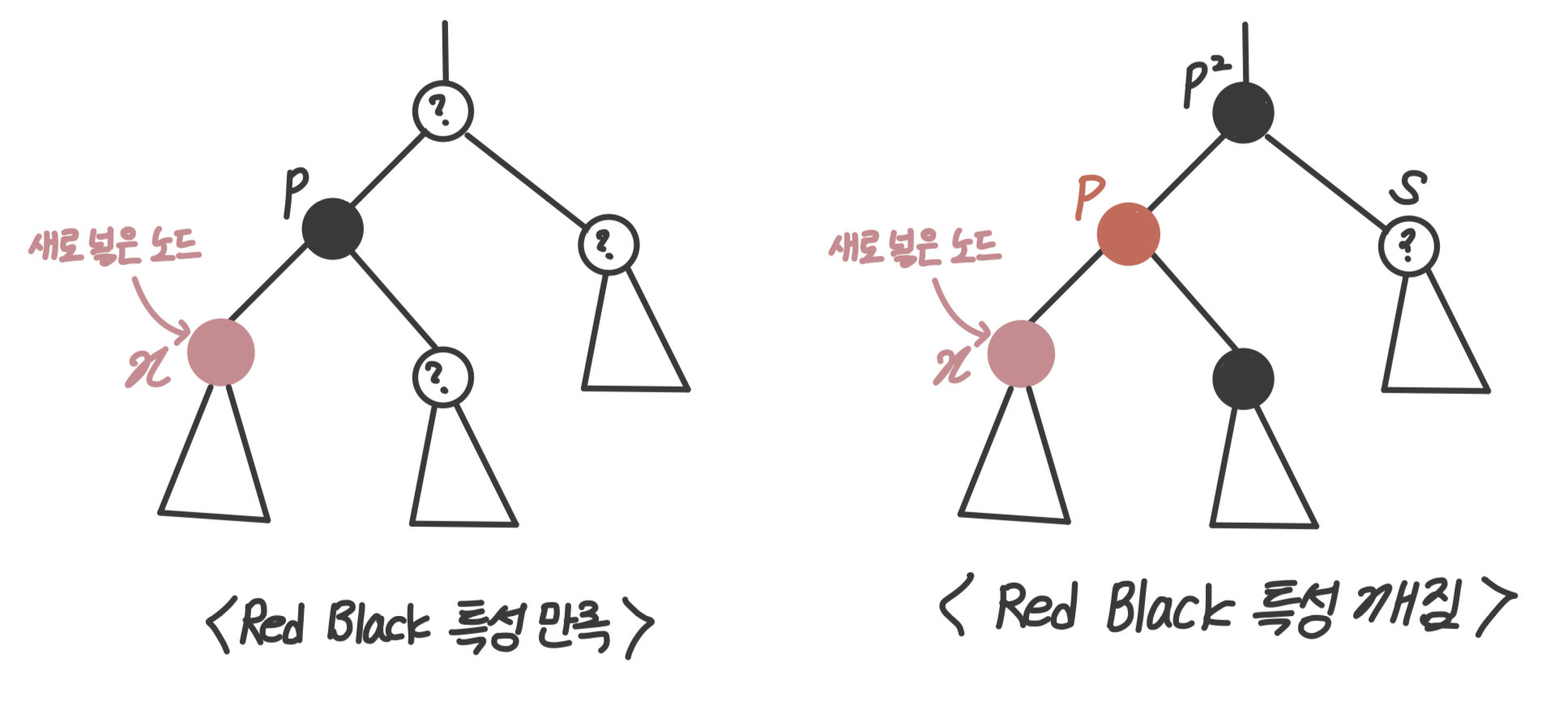
오른쪽처럼 레드블랙 특성이 깨지는 경우를 더 자세히 보자. 그 전에 notation은 아래처럼 정한다.
- : 새로 넣은 노드
- : x의 부모노드
- : p의 형제노드
- : p의 부모노드
가 레드일 때, 와 의 형제노드는 반드시 블랙임을 알 수 있다.
그리고 아래처럼 경우의 수를 나눠서 본다.
- Case1 : 가 레드인 경우
- Case2 : 가 블랙인 경우
- case2-1 : 가 블랙이고, 가 의 오른쪽 자식인 경우
- case2-2 : 가 블랙이고, 가 의 왼쪽 자식인 경우
Case1 : 가 레드일 때
- 레드 를 블랙으로 바꾼다.
- 블랙 를 레드로 바꾼다.
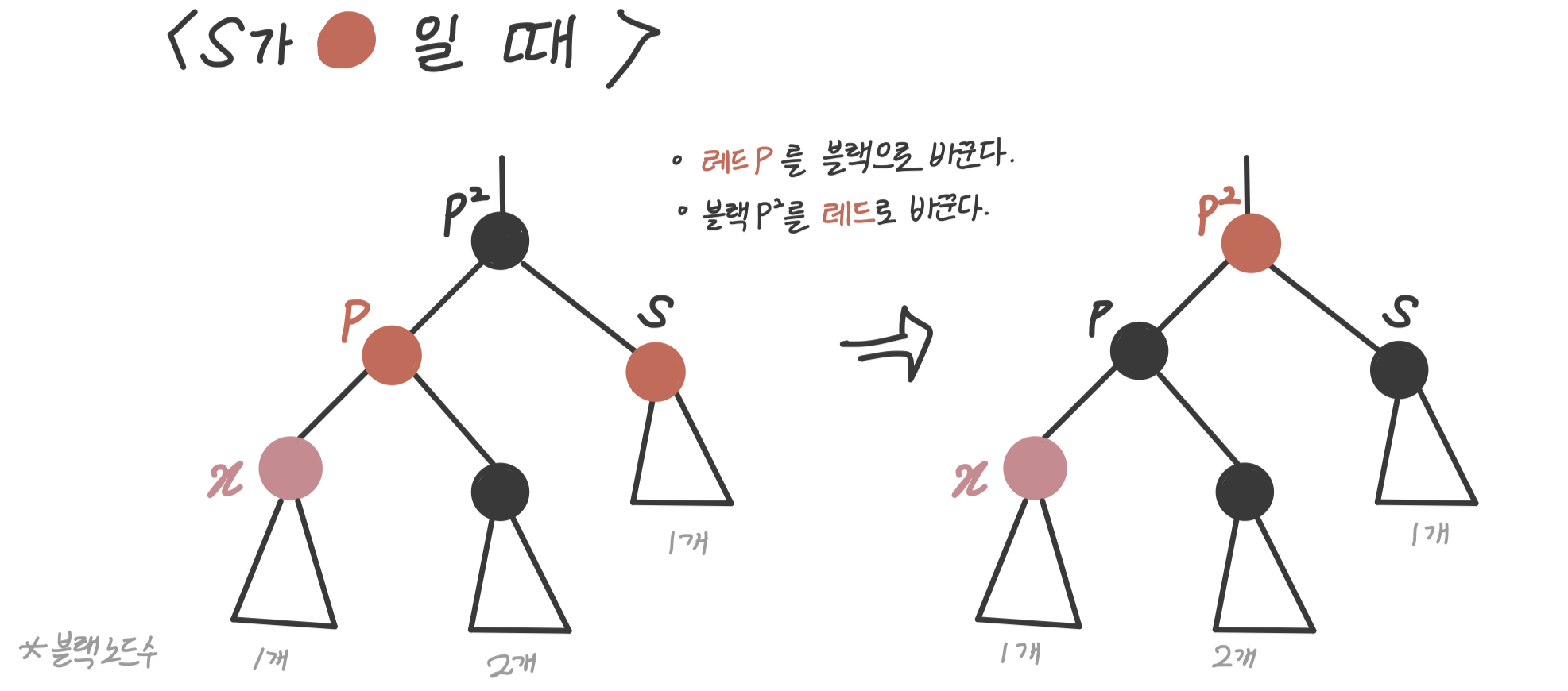
블랙 노드수는 1개, 2개, 1개로 바뀌지 않았다. (레드블랙 특성 4 유지)
반면, 위에 어떤 노드가 있을지 모른다. 레드노드가 있다면, 특성 3을 위반하는 문제가 또 발생하는 것이다. 이걸재귀적 문제(recursive problem)이라고 하고, 똑같이 반복해주면 된다.
부모노드가 블랙인 경우에 멈추면 되는데, 루트노드는 항상 블랙이니 루트노드까지 가서 멈출 수도 있다.
Case2 : 가 블랙일 때
이때는 또 두 가지 case2-1 과 case2-2로 나눠서 본다.
- case2-1 : 가 블랙이고, 가 의 오른쪽 자식인 경우
- case2-2 : 가 블랙이고, 가 의 왼쪽 자식인 경우
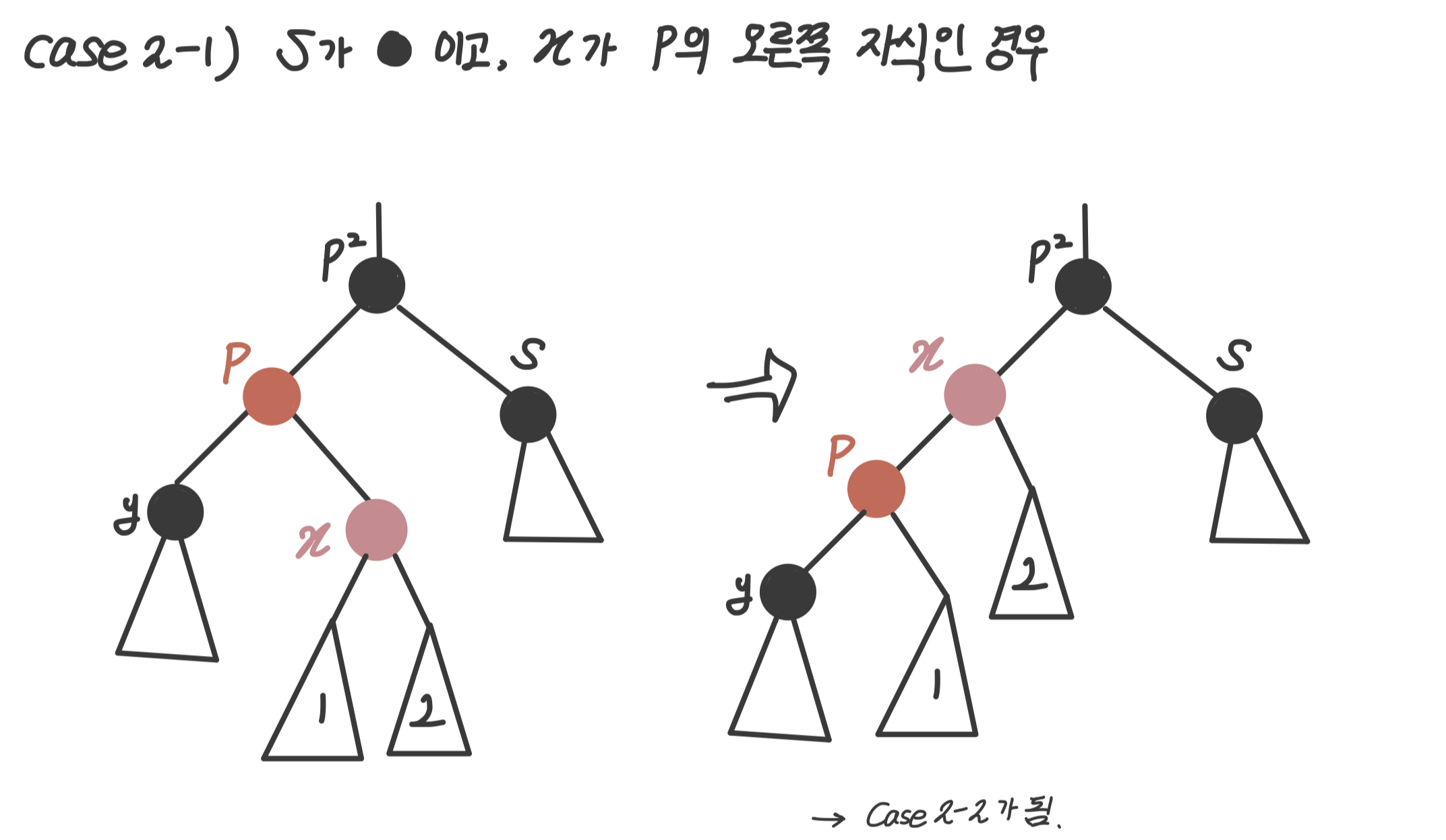
case2-1 : 가 블랙이고, 가 의 오른쪽 자식인 경우
- 의 왼쪽 노드를 로 만들고, 의 부모노드를 로 만든다.
- 의 오른쪽부분트리는 그대로 두고, 의 왼쪽부분트리를 의 오른쪽 자식으로 만든다.
-> 그럼 case2-2가 된다. case2-2로 가서 연산을 마저 수행한다.
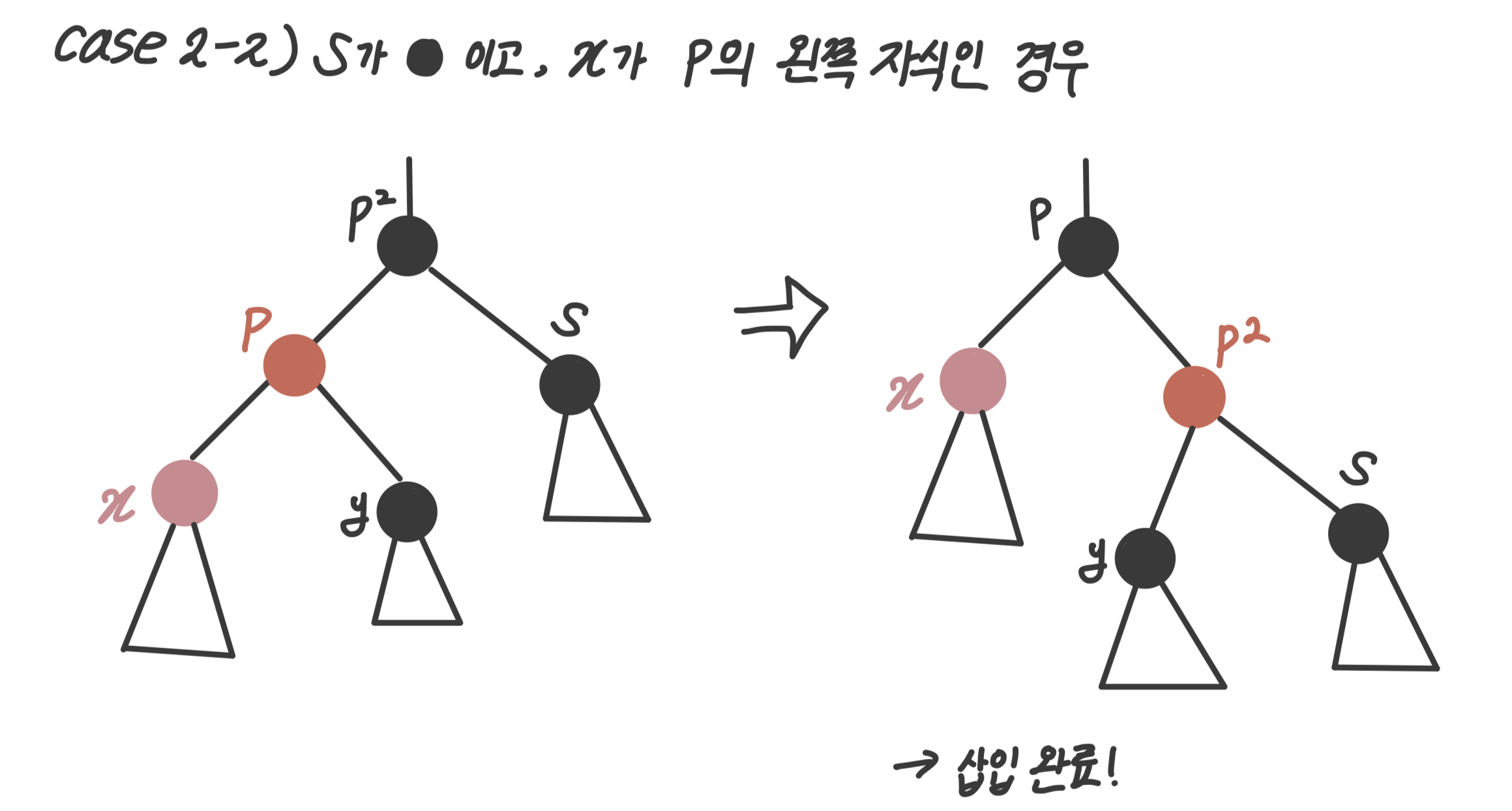
case2-2 : 가 블랙이고, 가 의 왼쪽 자식인 경우
- 회전하듯이 , , 의 위치를 다 바꿔준다.
- 블랙 노드 개수도 1, 2, 2개로 잘 유지되고 레드블랙 특성을 만족하면서 삽입이 완료된다.
📙 RB tree의 삭제연산
삭제연산도 마찬가지로 여러 경우를 생각해보아야 한다.
우선 아래 두 경우에는 그냥 지워주면 된다.
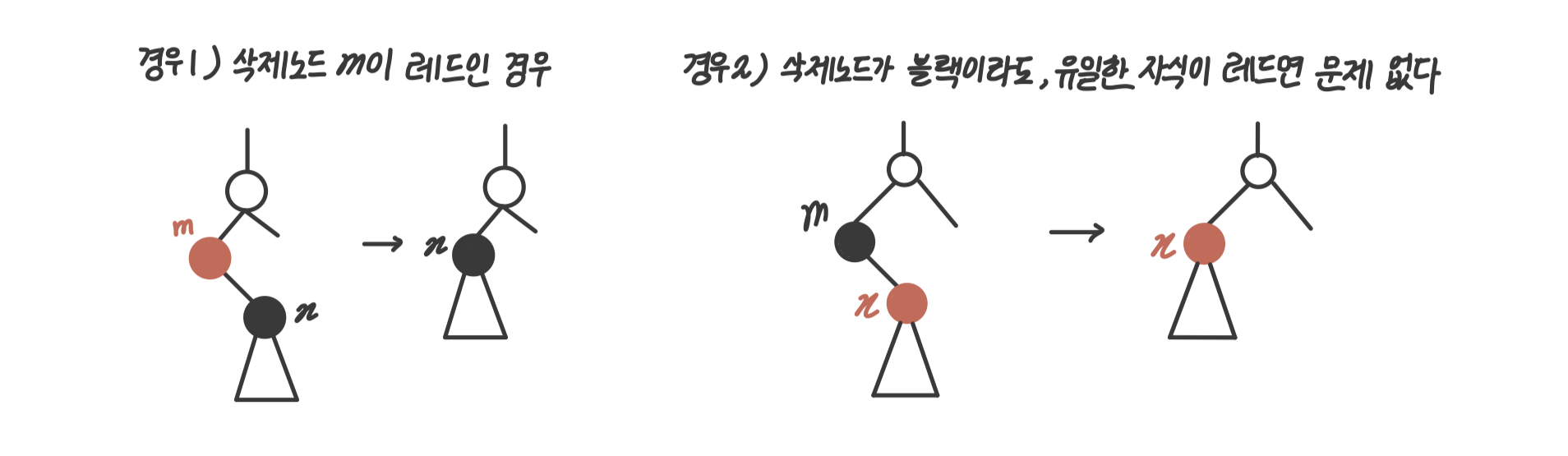
- 경우1 : 삭제 노드(m)가 레드면, 아무 문제 없다.
- 경우2 : 삭제 노드(m)가 블랙이라도 (유일한) 자식이 레드면 문제 없다.
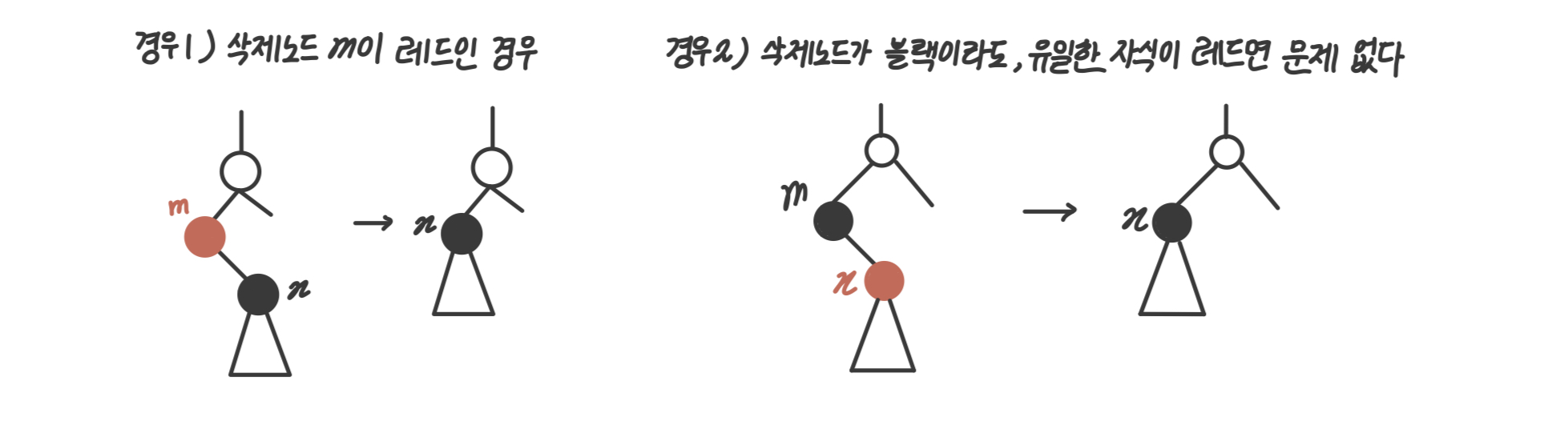
이제부터는 여러 Case 로 나눠서 고려해야 한다.
경우3 : 삭제노드(m)이 블랙이고, 유일한 자식도 블랙인 경우
이 경우 m을 삭제하면 그 루트에서 블랙 개수가 하나 부족해진다. 레드블랙 특성의 4번을 위반하게 된다. 이런 경우 x의 주변상황에 따라 처리 방법이 달라진다. Notation은 아래 사진을 참고하자.
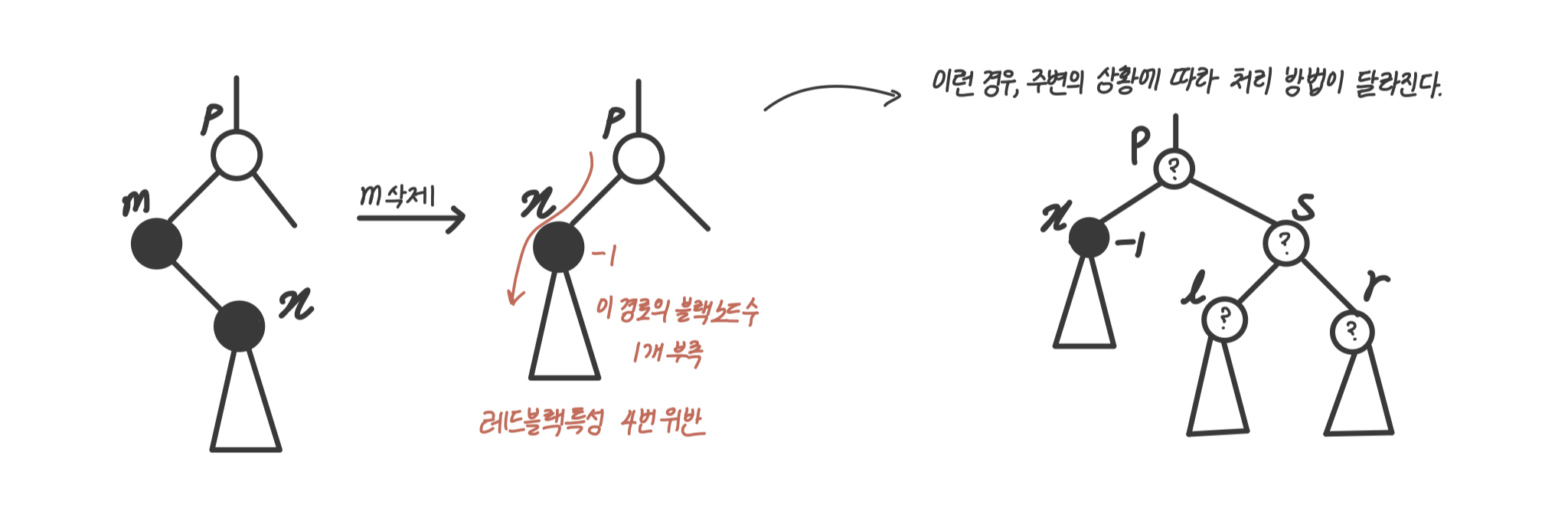
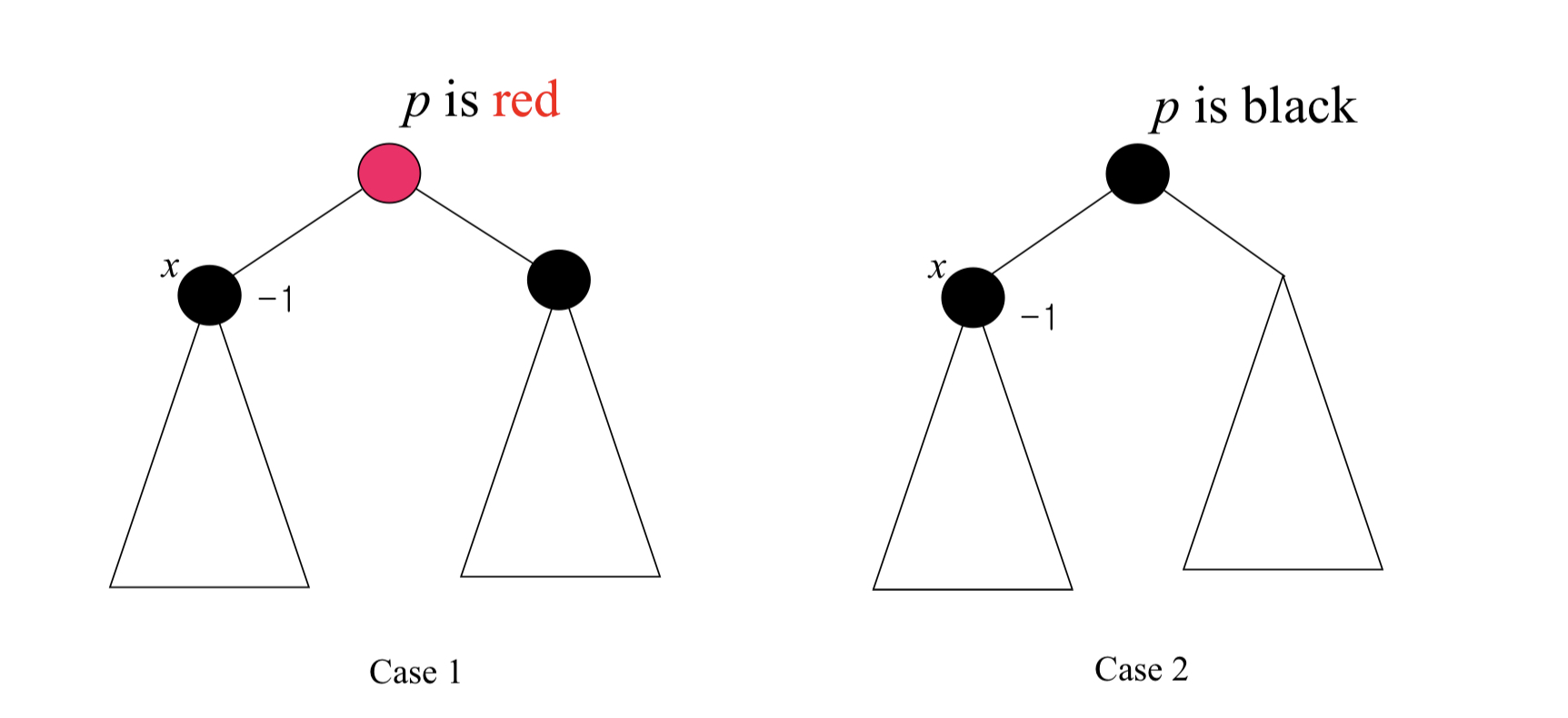
크게 아래처럼 두 Case로 나눌 수 있다.
- Case 1 : 부모노드 p가 레드인 경우 -> s노드는 무조건 블랙
- Case 2 : 부모노드 p가 블랙인 경우
이 두 가지의 경우 더 나뉘어진다. 아래처럼 7가지로 나눌 수 있는데, 같은 유형끼리 묶어서 최종적으로 5개로 묶어서 볼 수 있다. 각 5가지 경우에 어떻게 처리하는지 그림으로 봐보자.
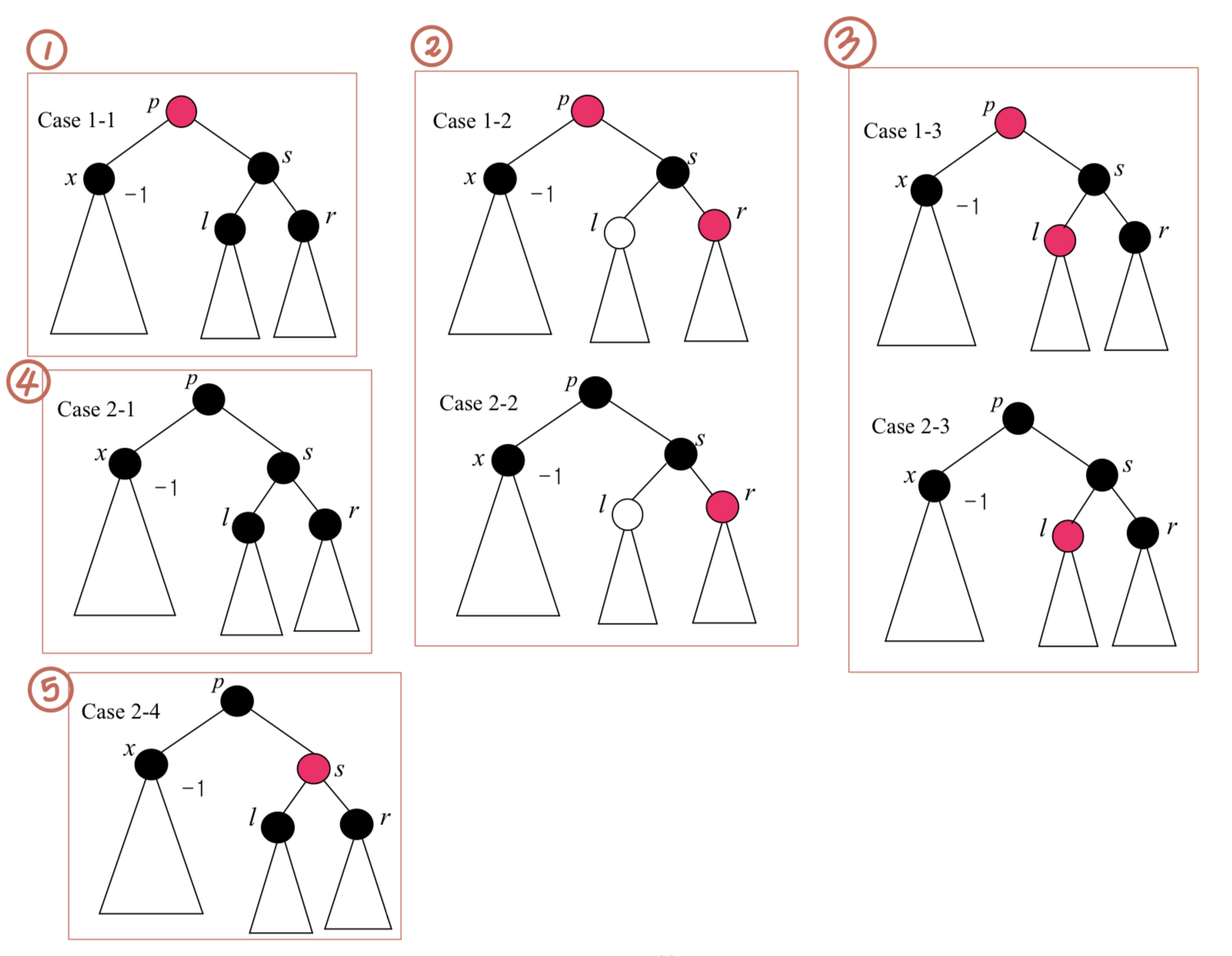
-
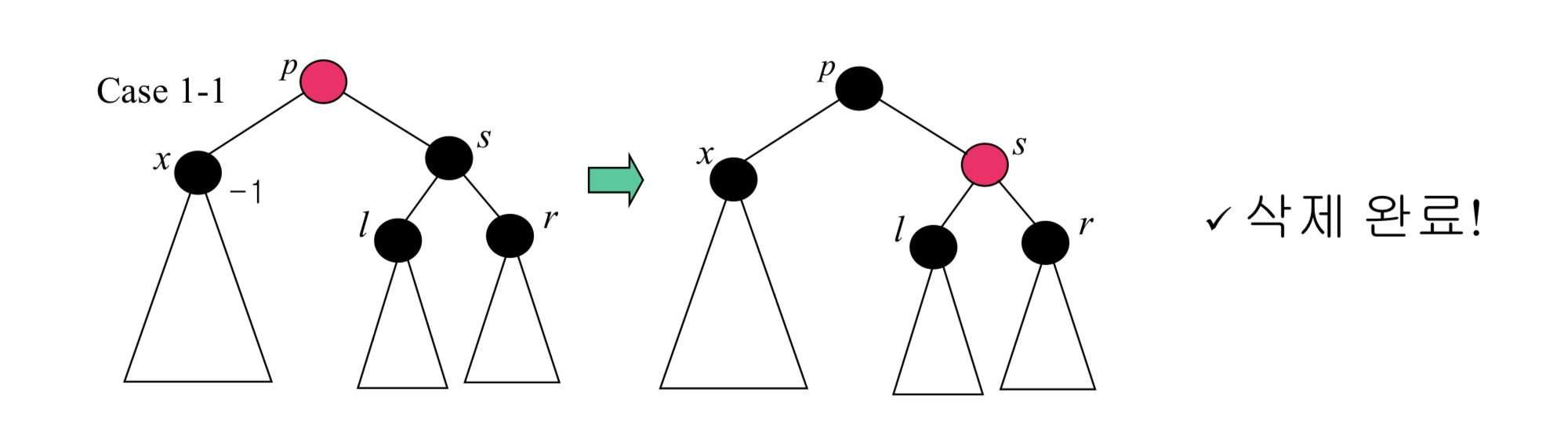
1번 : Case 1-1
- 레드인 p노드를 블랙으로 바꾸고, 블랙이던 s노드를 레드로 바꾼다.
이렇게 블랙 노드의 수를 맞춰줌으로써 삭제가 완료된다.
- 레드인 p노드를 블랙으로 바꾸고, 블랙이던 s노드를 레드로 바꾼다.
-
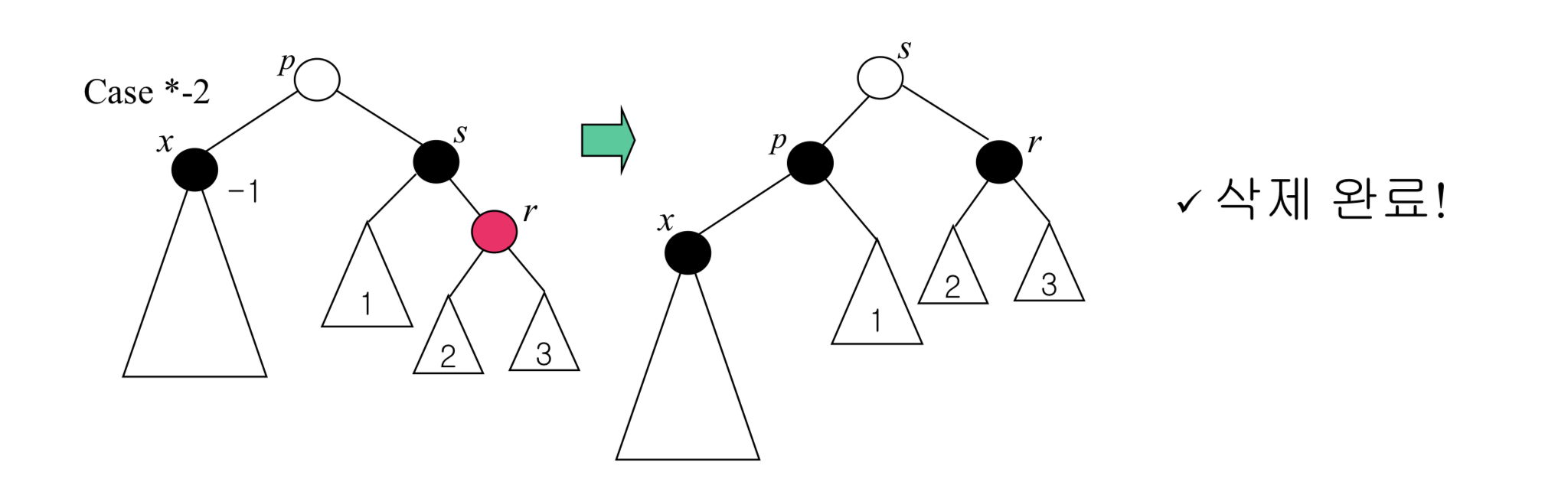
2번 : Case *-2
- p의 색은 상관없고, 블랙의 s 와 레드 r을 가진 상황이다.
이 경우 회전하듯, s를 루트노드로 만들어주어 블랙 노드 수를 맞춰준다. 삭제가 완료된다.
- p의 색은 상관없고, 블랙의 s 와 레드 r을 가진 상황이다.
-
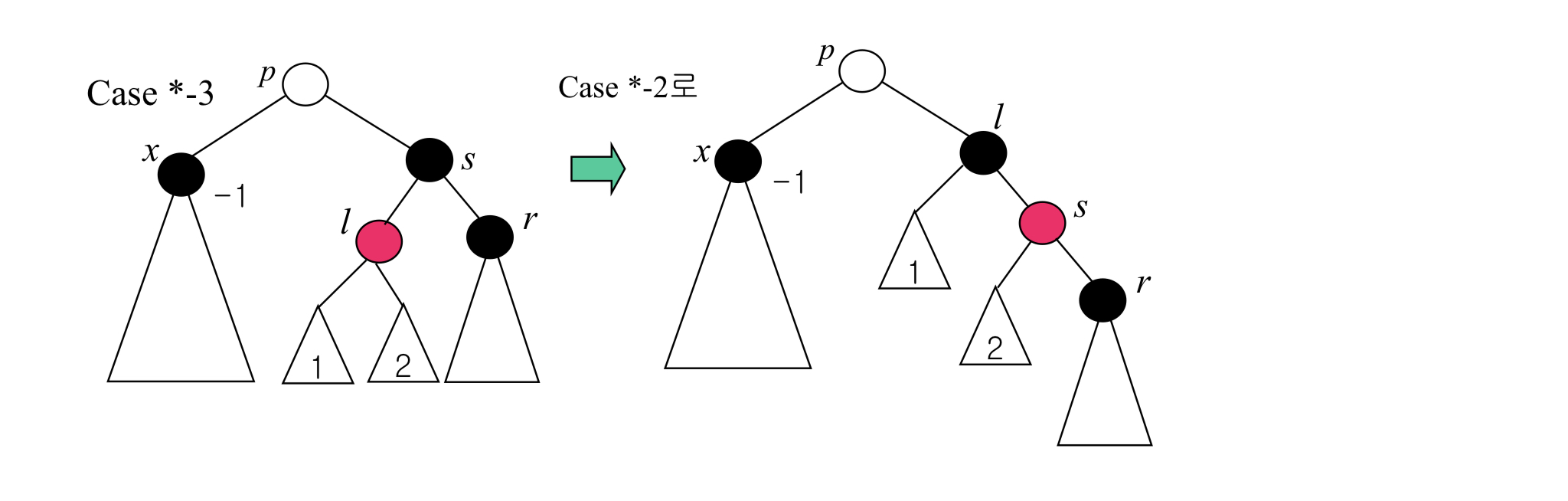
3번 : Case *-3
- 한번에 삭제가 완료되지 않는다.
- 삭제가 완료되지 않고 2번(
Case *-2)의 모습으로 바뀐다. - 2번으로 가서 같은 연산을 수행해준다.
-
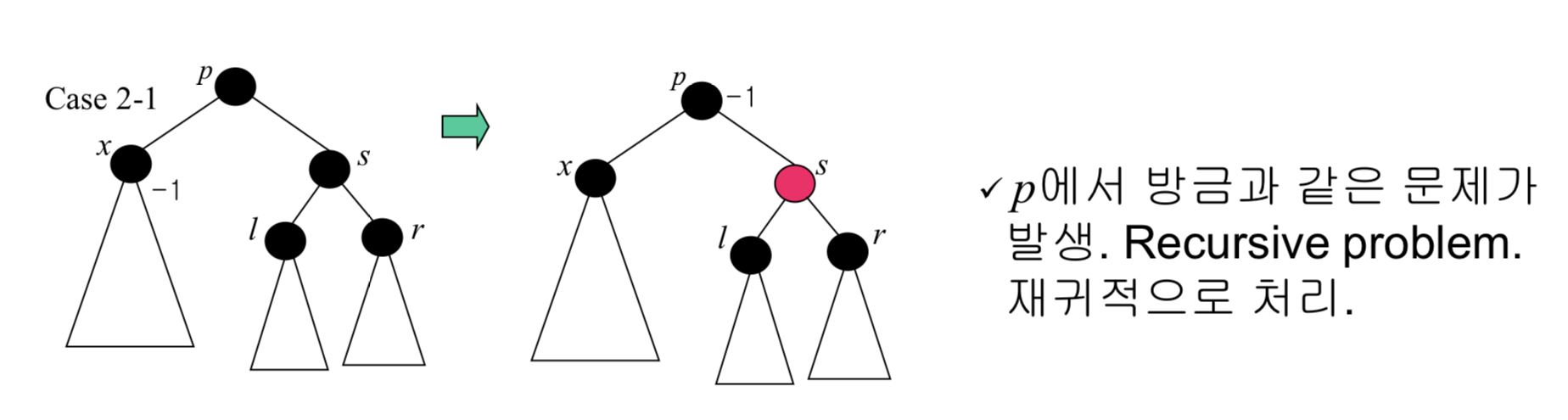
4번 : Case *-3
- 블랙이던 s를 레드로 바꿈으로써 블랙노드 수를 맞춰준다.
- 그러나 또 p에서 문제가 발생한다. p의 부모노드가 더 있다고 생각해보면 p를 지나는 경로에서 블랙노드 수가 하나 삭제가 된 것이다. 그럼 재귀적으로 윗부분을 계속 수정해주면 된다. 루트노드는 블랙이므로 언젠간 끝나게 되어 있다.
-
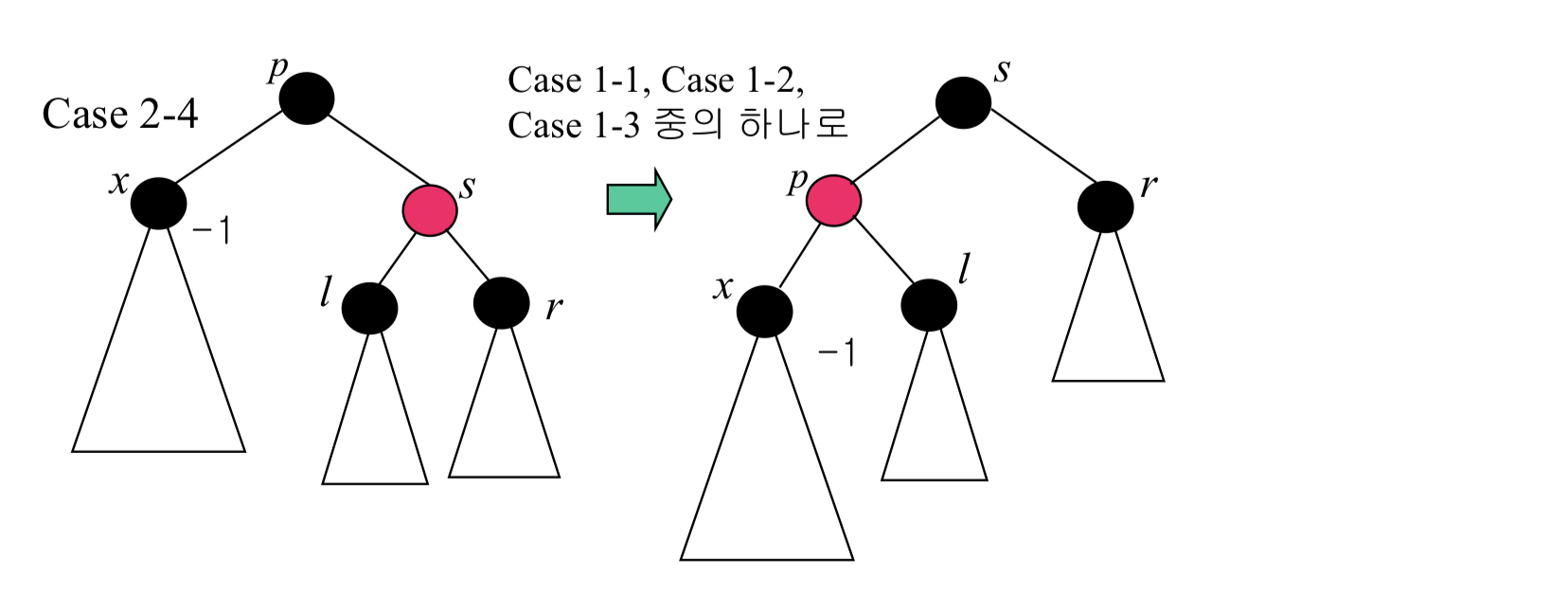
5번 : Case *-3
- 회전하여 노드를 옮겨준다. 그럼 Case1-1, Case1-2. Case1-3 중 하나로 바뀐다. 해당 상황에 맞는 번호로 가서 연산을 수행해주면 된다.
이렇게 Red-Black Tree에서의 탐색과 삭제연산을 그림으로 알아봤다. 이후에는 파이썬 코드 구현을 추가하겠다.

좋은 글 감사합니다. 참고해서 공부하기 정말 편하네요!!