0️⃣ MST란?
MST(Minimum Spanning Tree)는 최소신장트리 또는 최소 비용 걸침 나무라고 하는데, 그래프의 신장트리들 중 간선의 합이 최소인 신장트리를 의미한다.
1. 입력조건
'무향 연결 그래프'여야 한다.
- 무향 : 방향이 없는 경우
- 연결 : 그래프가 나뉘어 있지 않음. 모든 정점 간에 경로가 존재함.
2. 신장트리 = 걸침나무
- 트리
- 싸이클이 없는 연결 그래프를 말한다.
- n개의 정점(node)을 가진 트리는 항상 n-1개의 간선(edge)을 갖는다.
- 신장트리(걸침나무, Spanning Tree)
- 그래프의 정점들과 간선들로만 구성된 트리이다.
아래처럼 여러 개의 신장트리를 만들 수 있고, 그 중 노드를 잇는 가중치를 가장 작게 만드는 신장트리를Minimum Spanning Tree라고 한다.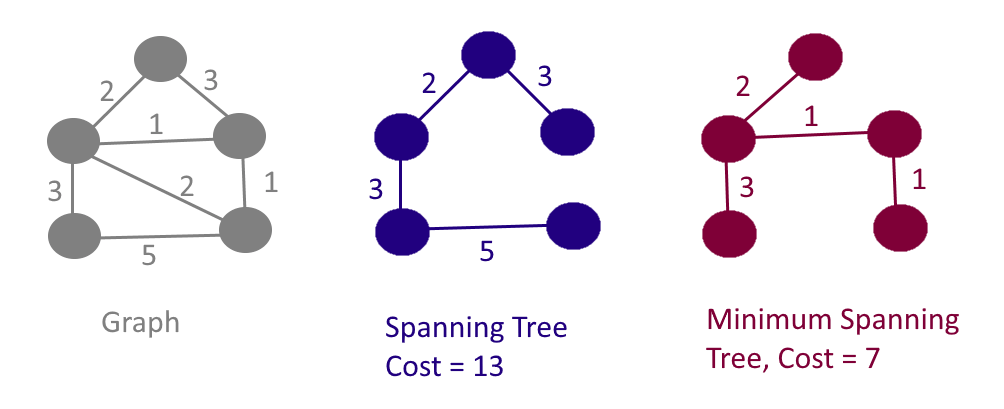
- 그래프의 정점들과 간선들로만 구성된 트리이다.
1️⃣ Prim Algorithm
✔️ Prim 수도코드와 이해
Prim의 수도코드
먼저 Prim 알고리즘의 수도코드를 보자.
Prim(G, r)
{
S <- {}
정점 r을 방문했다고 표시하고 집합 S에 포함시킨다.
while (S != V){
S에서 V-S를 연결하는 간선들 중 최소길이의 간선(x, y)를 찾는다;
정점 y를 방문했다고 표시하고, 집합 S에 포함시킨다;
}
}Prim의 이해
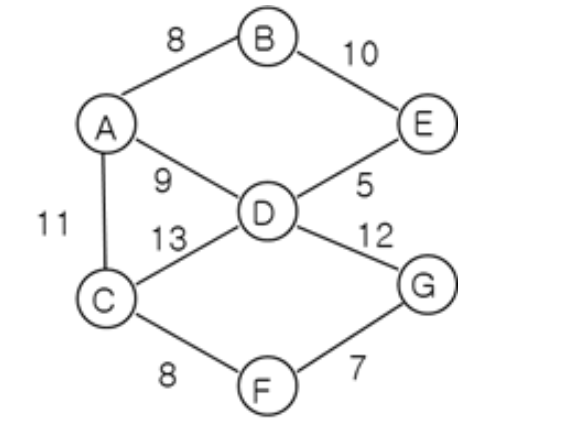
- 위 수도코드와 아래 연결그래프를 보며 이해해보자.
- G는 그래프, r은 시작노드 A, V는 전체 노드이다.
- S = {A}이고, V-S는 아직 방문하지 않은 노드들이다. S에서 V-S를 연결하는 간선은 A-B, A-D, A-C이고 그 중 최소길이인 A-B를 찾았다.
- B를 방문집합 S에 포함시킨다. S = {A, B}
- 또 S에서 V-S를 연결하는 간선인 A-C, A-D, B-E 중 최소길이인 A-D를 찾았다. D를 방문집합 S에 포함시킨다. S = {A, B, D}
- S == V가 될때까지 반복
Prim의 특징
- Rrim 알고리즘은 그리디(greedy) 알고리즘의 일종이다.
- 그리디 알고리즘은 순간순간의 최적만 찾기 때문에 전역 최적해를 보장하지 않는다. 그러나 그리디 알고리즘 중 Prim은 전역최적해를 보장하는 드문 예시이다.
- 수행시간 : 이다. log인 이유는 최소간선을 찾을 때 정렬을 쓰는데 이때 heap정렬을 쓰면 log|V|가 된다.
✔️ Prim 구현(python)
입력
위 사진과 동일한 가중치가 존재하는 그래프는 아래처럼 dictionary 안에 dictionary 형태로 표현할 수 있다.
mywgraph = { "A" : {"B":8, "C":11, "D":9},
"B" : {"A":11, "E":10},
"C" : {"A":11, "D":13, "F":8},
"D" : {"A":9, "C":13, "E":5, "G":12},
"E" : {"B":10, "D":5},
"F" : {"C":8, "G":7},
"G" : {"D":12, "F":7}
}Prim 구현(Python)
def Prim(G, r) :
conn = [] # 간선이 추가된 순서
S = [r] # 방문한 노드 리스트
while len(S) != len(G):
xmin, ymin, min_value = find_min_edge(S, G) # 최소 간선 찾기
S.append(ymin)
conn.append([xmin, ymin, min_value])
return conn
def find_min_edge(S,G): # 최소 간선 찾기
edges = []
for x in S:
for y in G[x]:
if y not in S:
edges.append([x, y, G[x][y]])
xmin, ymin, min_value = min(edges, key = lambda x:x[-1])
return xmin, ymin, min_value
Prim(mywgraph, "A")
"""
[['A', 'B', 8],
['A', 'D', 9],
['D', 'E', 5],
['A', 'C', 11],
['C', 'F', 8],
['F', 'G', 7]]
"""2️⃣ Kruskal Algorithm
✔️ Kruskal 수도코드와 이해
Kruskal의 수도코드
Kruskal(G)
{
T <- {}; // T는 신장트리
단 하나의 정점만으로 이루어진 n개의 집합을 S로 초기화 한다;
모든 간선을 가중치가 작은 순으로 정렬한다;
while (T의 간선수 < n-1){
최소비용 간선 (u, v)를 제거한다;
정점 u와 정점 v가 서로 다른 집합에 속하면{
두 집합을 하나로 합친다;
T <- T + {(u, v)};}
}
}
Kruskal의 이해
- Kruskal 작동예시
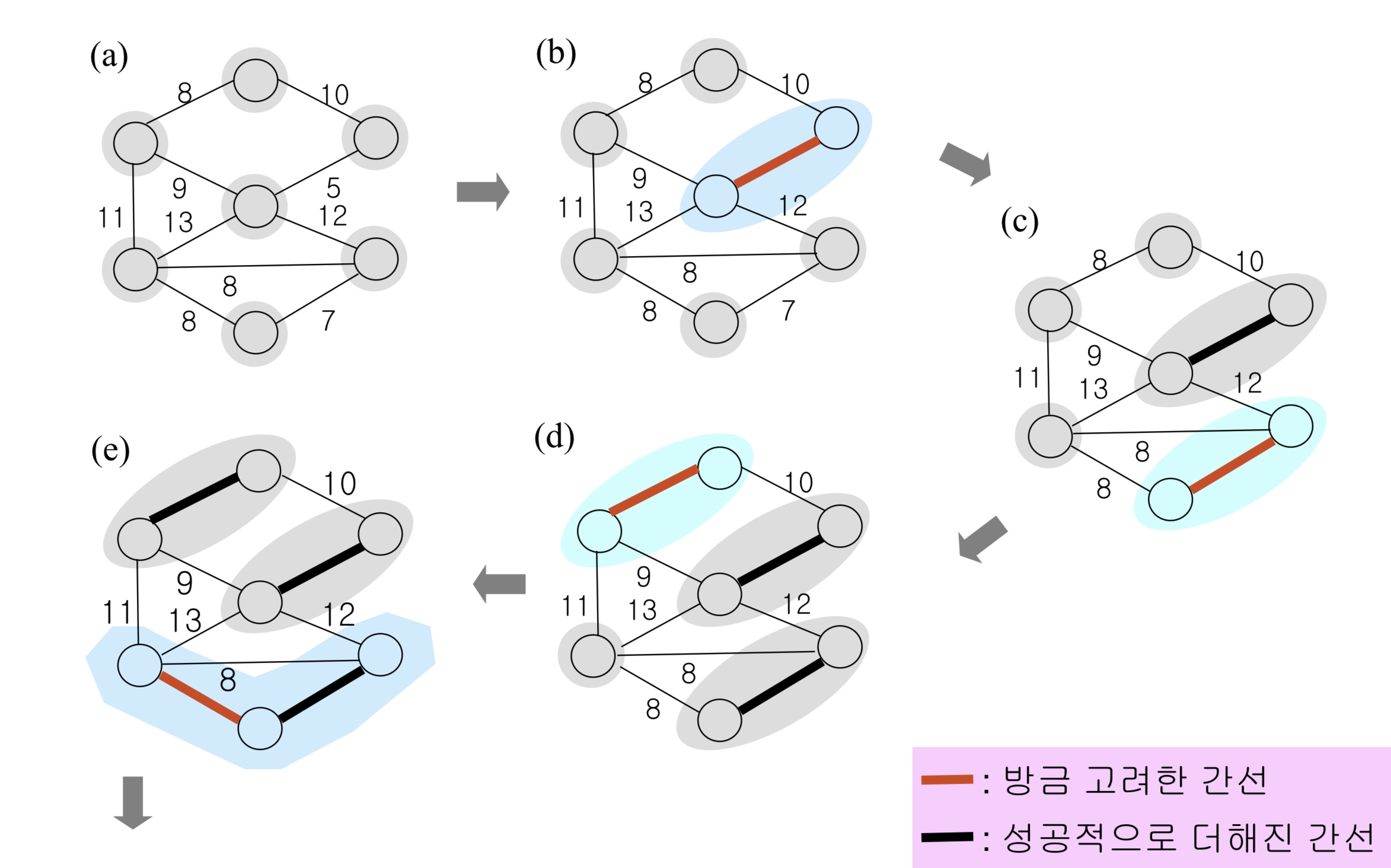
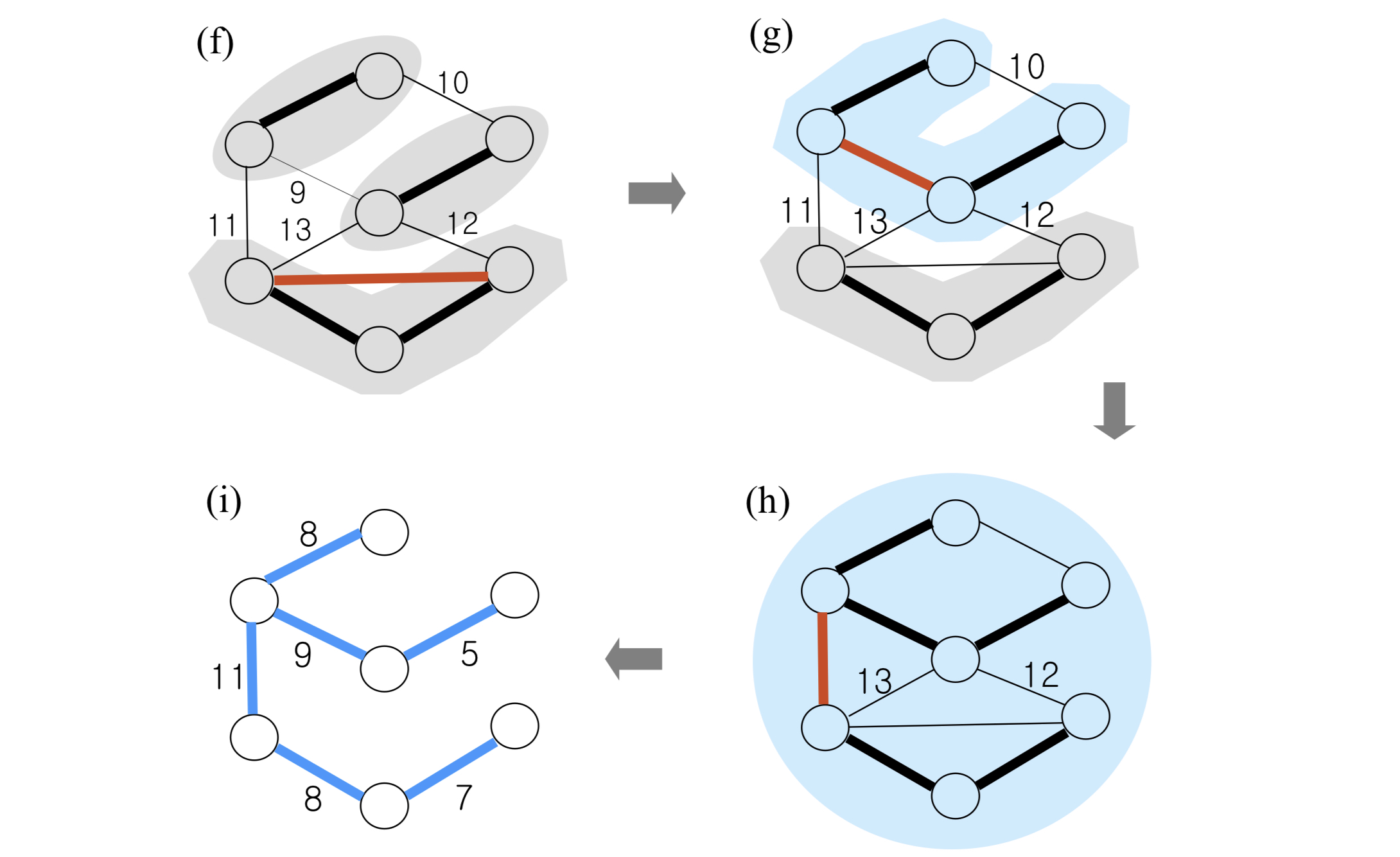
- 계층적 클러스터링과 방식이 유사하다. 최소간선을 찾아 같은 집합으로 묶고 그 다음 최소간선을 묶고..를 반복하는데 이때 사이클이 생기면 안되므로 서로 다른 집합에 속할 때만 묶어준다.
✔️ Kruskal 구현(python)
입력
위와 동일
Kruskal 구현(python)
def Kruskal(G):
T = []
S = [set(x) for x in G.keys()]
print("S=", S)
E = sort_edges(G)
while len(T) < len(G)-1:
edge, value = E.popitem() # 작은 맨 뒤 삭제
u, v = list(edge)
if any(u in subset and v in subset for subset in S) == False: # 정점 u와 v가 서로 다른 집합에 속하면
# u가 있는 집합과 v가 있는 집합 합치기
merged_set = set()
for s in S:
if u in s:
merged_set.update(s)
elif v in s:
merged_set.update(s)
S = [merged_set] + [s for s in S if u not in s and v not in s]
print("S=", S)
T.append([set(edge), value])
return T
def sort_edges(G):
E = {}
for k1,v1 in G.items():
for k2,v2 in v1.items():
E[frozenset([k1,k2])] = v2
E = {k: v for k, v in sorted(E.items(), key=lambda item: item[1], reverse=True)}
return E # {frozenset({'C', 'D'}): 13, frozenset({'D', 'G'}): 12, frozenset({'B', 'A'}): 11, frozenset({'C', 'A'}): 11, frozenset({'E', 'B'}): 10, frozenset({'A', 'D'}): 9, frozenset({'F', 'C'}): 8, frozenset({'F', 'G'}): 7, frozenset({'E', 'D'}): 5}
print(Kruskal(mywgraph))
"""
S= [{'A'}, {'B'}, {'C'}, {'D'}, {'E'}, {'F'}, {'G'}]
S= [{'E', 'D'}, {'A'}, {'B'}, {'C'}, {'F'}, {'G'}]
S= [{'F', 'G'}, {'E', 'D'}, {'A'}, {'B'}, {'C'}]
S= [{'F', 'C', 'G'}, {'E', 'D'}, {'A'}, {'B'}]
S= [{'E', 'A', 'D'}, {'F', 'C', 'G'}, {'B'}]
S= [{'E', 'B', 'A', 'D'}, {'F', 'C', 'G'}]
S= [{'E', 'C', 'A', 'F', 'B', 'D', 'G'}]
[[{'E', 'D'}, 5], [{'F', 'G'}, 7], [{'F', 'C'}, 8], [{'A', 'D'}, 9], [{'E', 'B'}, 10], [{'C', 'A'}, 11]]
"""frozenset을 쓰는 이유?
아래처럼 key는 간선, value는 가중치로 표현하는 dictionary를 만들고 싶다.
di = {{'D', 'E'} = 2,
{'D', 'A'} = 3}근데 아래처럼 set을 key로 쓰게 되면 오류가 난다.
di = {}
di[{'D', 'E'}] = 2
di
# TypeError: unhashable type: 'set'그래서 frozenset을 key로 쓰는 것이다.
di = {}
di[frozenset(['D', 'E'])] = 2
di # {frozenset({'D', 'E'}): 2}