0️⃣ 그래프 기초
✔️ 그래프의 종류와 표현
그래프는 가중치가 있는지, 방향이 있는지에 따라 다르게 표현한다.
- 가중치 여부에 따라
- 가충치 그래프
- 가중치가 없는 그래프
- 방향 여부에 따라
- 유향 그래프
- 무향 그래프
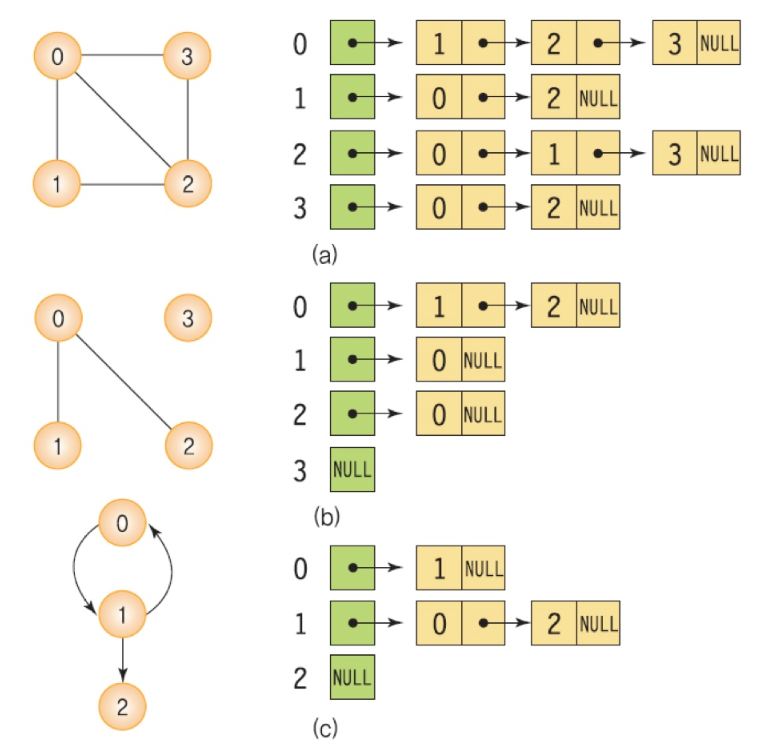
각 그래프를 '인접행렬'로는 어떻게 표현하는지 보자
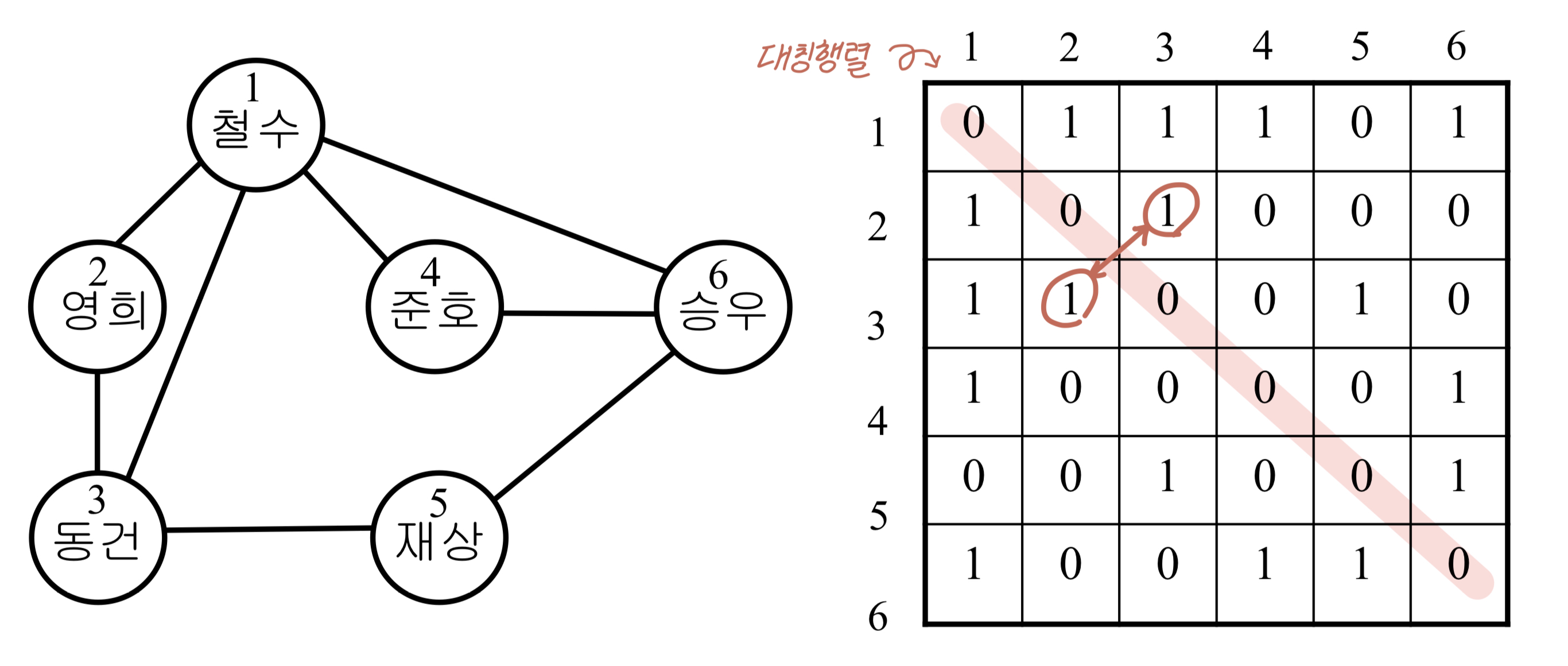
- 무향 그래프
- 인접행렬은
대칭행렬
- 인접행렬은
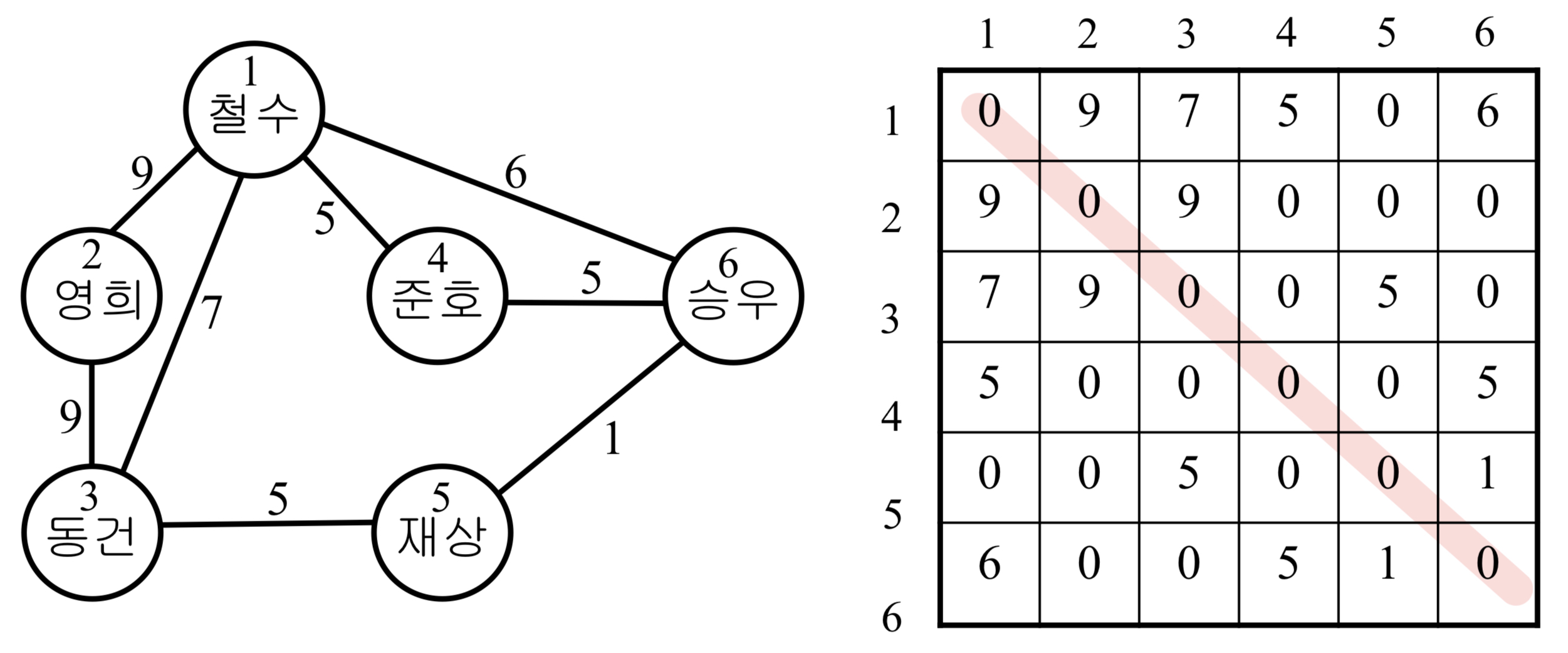
- 가중치가 있는 무향 그래프
- 인접행렬은
대칭행렬, 가중치가 표현되어 있다.
- 인접행렬은
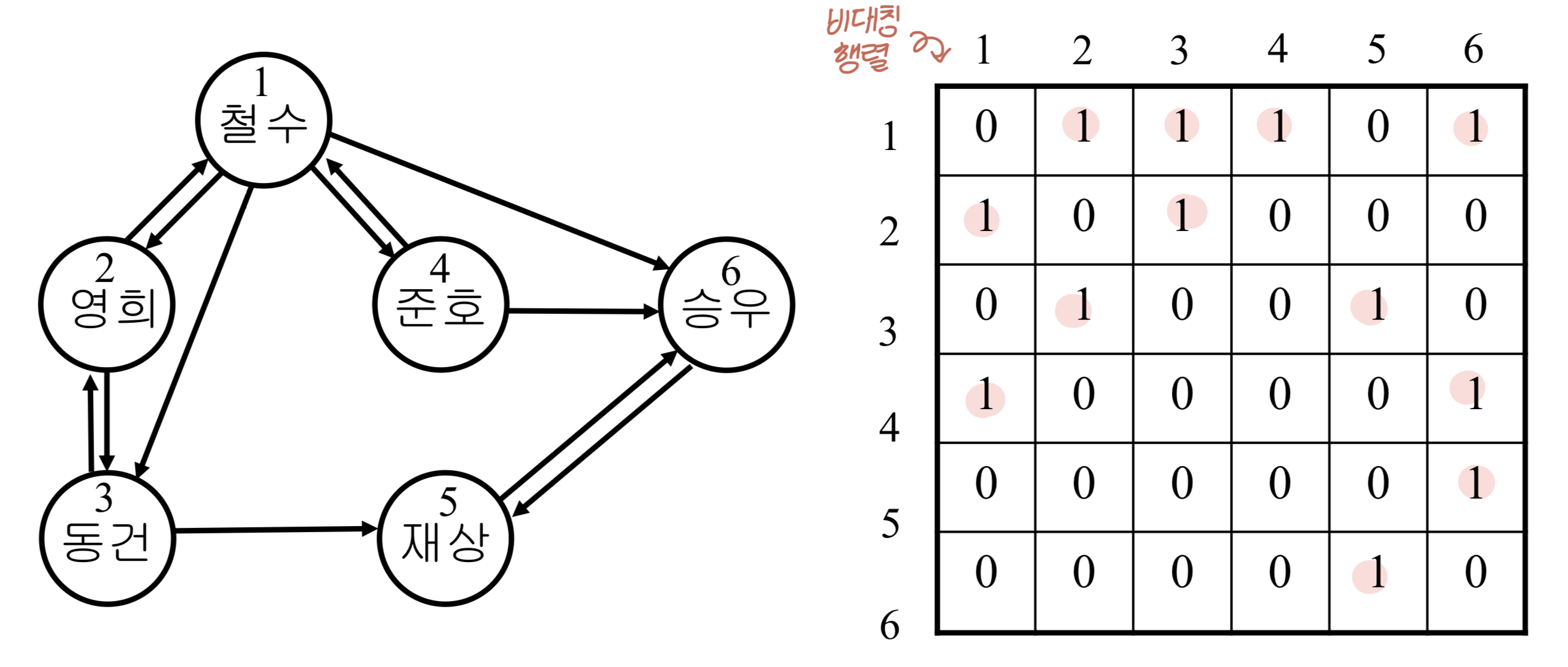
- 유향 그래프
- 인접행렬은
비대칭행렬 - 세로가 From, 가로가 To
- 인접행렬은
- 가중치가 있는 유향 그래프
- 인접행렬은
비대칭행렬, 가중치가 표현
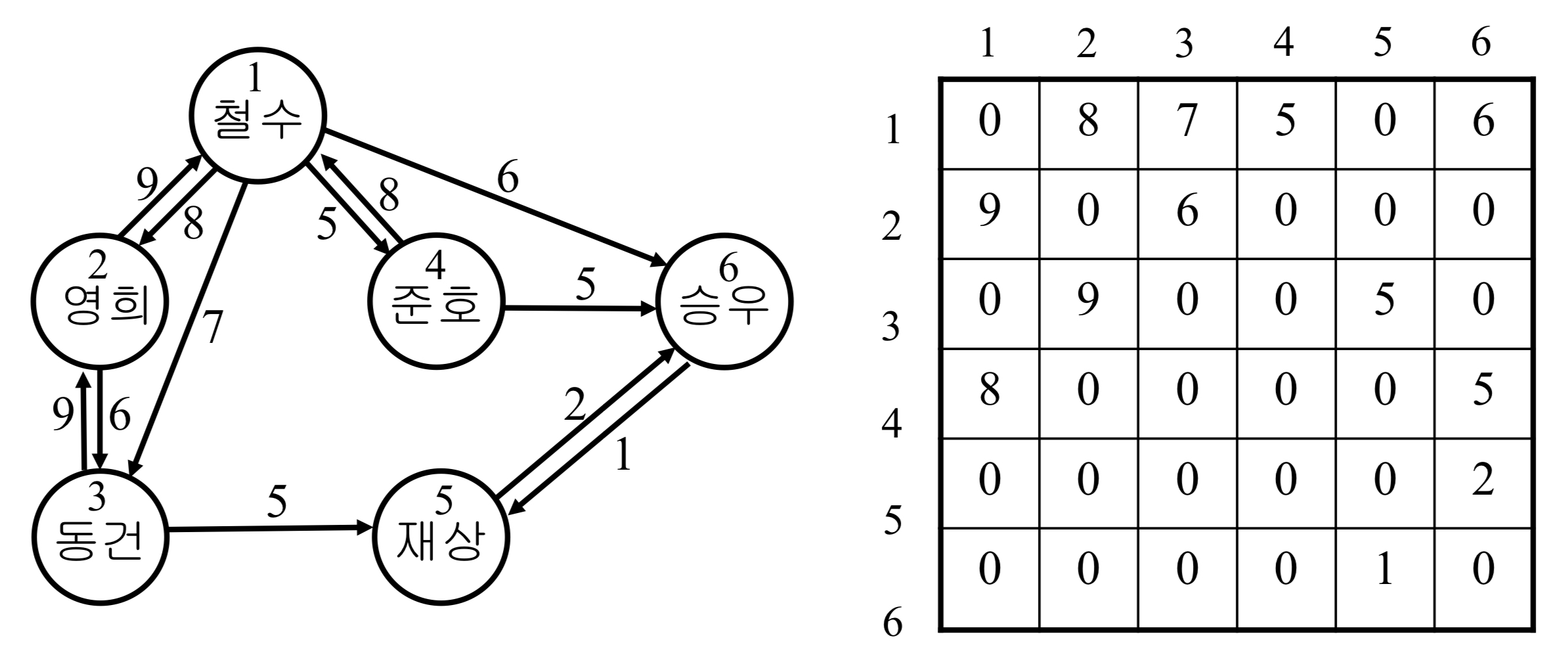
- 인접행렬은
✔️ 인접행렬, 인접리스트
그래프를 표현하는 데에는 두 가지 방법이 있다. 위처럼 행렬로 표현할 수도 있고 인접리스트로도 표현할 수 있다.
인접행렬(Adjacency Matrix)
노드의 개수가 N 일때, NxN 행렬로 표현한다.
matrix = [[0, 1, 1],
[1, 0, 0],
[1, 0, 1]]if ((i,j) exists)
A[i][j] = W_ij
else if (i==j) A[i][j] = 0
else A[i][j] = infinity # i,j 간 에지가 존재하지 않는 경우인접리스트(Adjacency List)
- 각 정점에 인접한 정점들을 연결 리스트로 표현한다. 정점이 n개인 그래프라면 n개의 연결리스트로 구성한다. 각 연결리스트마다 포인터 변수가 리스트의 처음 노드를 가리키며 연결리스트가 없는 경우, 즉 차수가 0인 경우 포인터 변수의 값은 null이 된다.
# 1번 예시 ad_list = {0: {1,2}, 1: {0}, 2: {0,1}, 3: {0}} # value를 set이 아니라 [] 리스트로 표현해도 된다.
1️⃣ DFS
DFS와 BFS의 개념은 여기에서 확인할 수 있다.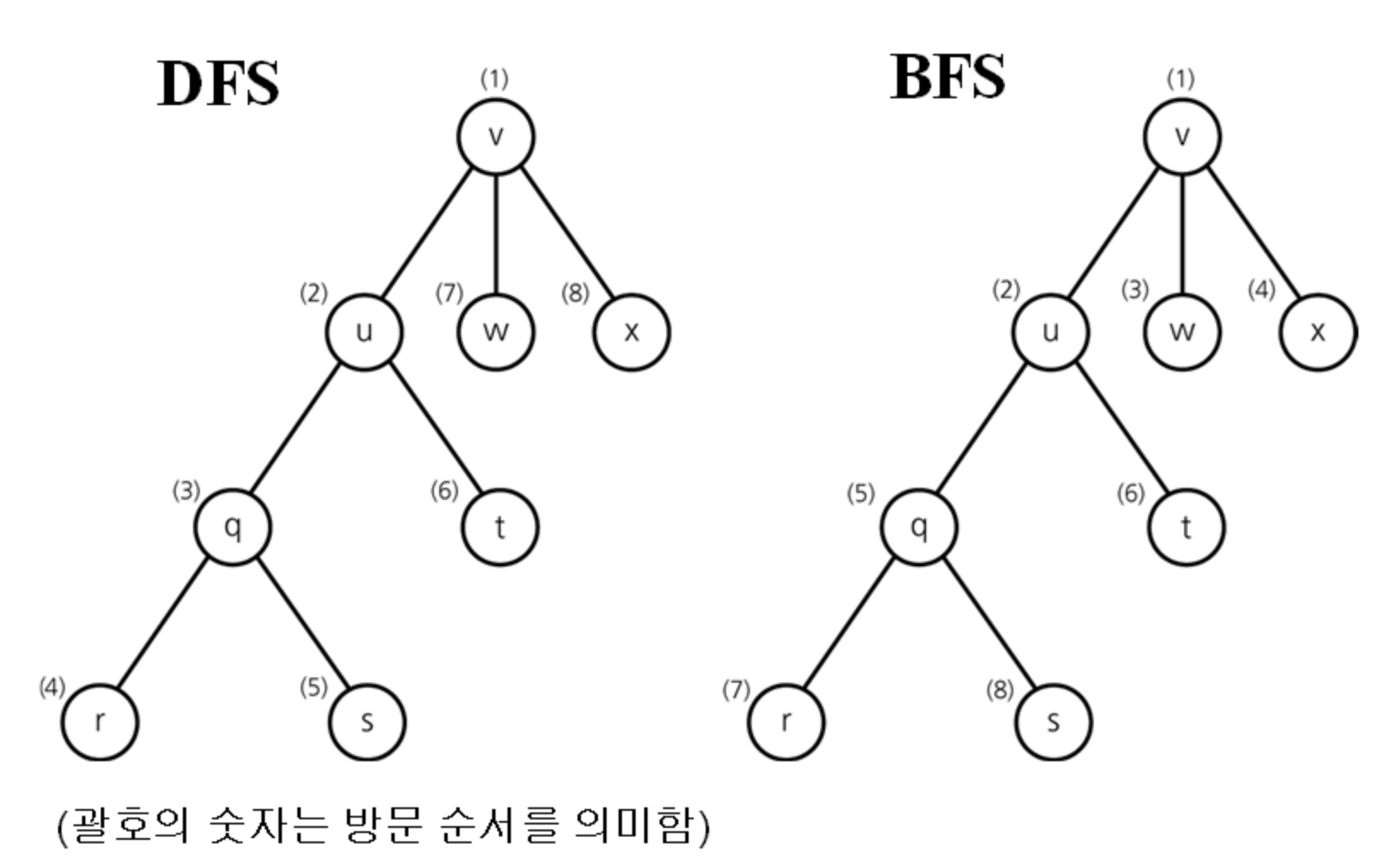
✔️ 인접리스트에서의 DFS
위 트리를 표현하는 인접리스트는 아래와 같다.
입력
mytree = { "v" : {"u", "w", "x"},
"u" : {"q", "t"},
"w" : {},
"x" : {},
"q" : {"r", "s"},
"t" : {},
"r" : {},
"s" : {}
}# 인접리스트 입력방식에서 DFS구현하기
def DFS(G): # 깊이우선탐색 알고리즘
visited = []
for v in G.keys():
if v not in visited:
aDFS(G, v, visited)
return visited
def aDFS(G, v, visited): # 깊이우선탐색 알고리즘
visited.append(v)
for x in G[v]:
if x not in visited:
aDFS(G, x, visited)
print("DFS:", DFS(mytree)) # DFS: ['v', 'w', 'u', 'q', 's', 'r', 't', 'x'] (value를 set으로 설정해서 이 순서는 다르게 나올 수 있음.)✔️ 인접행렬에서의 DFS
인접행렬은 아래럼 만들 수 있다.
입력
N1 = {0:'q', 1:'r', 2:'s', 3:'t', 4:'u', 5:'v', 6:'w', 7:'x'}
A1 = [[0,1,1,0,0,0,0,0],
[0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0],
[1,0,0,1,0,0,0,0],
[0,0,0,0,1,0,1,1],
[0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0]]
G1 = (N1, A1)# 인접행렬 입력방식에서 DFS구현하기
def DFS_tbl(G, v): # 깊이우선탐색 알고리즘 (v부터 시작하게 세팅)
visited = []
stack = [v]
while stack: # stack이 비어있지 않으면,
node = stack.pop()
if node not in visited:
aDFS_tbl(G, node, visited)
return visited
def aDFS_tbl(G, v, visited): # 깊이우선탐색 알고리즘
visited.append(v)
for i in range(len(G[1])):
if i not in visited and G[1][v][i] == 1:
aDFS_tbl(G, i, visited)
def idx_to_key(list, N):
keys =[]
for i in list:
keys.append(N[i])
return keys
idxs = DFS_tbl(G1, 5)
print(idxs, idx_to_key(idxs, N1)) # [5, 4, 0, 1, 2, 3, 6, 7] ['v', 'u', 'q', 'r', 's', 't', 'w', 'x']2️⃣ BFS
✔️ 인접리스트에서의 BFS
# 인접리스트 입력방식에서 BFS구현하기 Ver.1
def BFS(G, s):
visited = []
queue = [s]
while queue: # 큐가 비어있지 않으면,
node = queue.pop(0)
if node not in visited:
visited.append(node)
queue.extend(G[node])
return visited
print(BFS(mytree, "v")) # ['v', 'w', 'u', 'x', 'q', 't', 's', 'r']# 인접리스트 입력방식에서 BFS구현하기 Ver.2
import queue
def BFS(G, s):
visited = [s]
q = queue.Queue()
q.put(s)
while not q.empty(): # 큐가 비어있지 않으면,
node = q.get()
for v in G[node]:
if v not in visited:
visited.append(v)
q.put(v)
return visited
print(BFS(mytree, "v"))✔️ 인접행렬에서의 BFS
from collections import deque
def BFS_tbl(G, s):
visited = [] # s에 방문 표시
queue = [s]
while queue:
node = queue.pop(0)
if node not in visited:
visited.append(node)
for i in range(len(G[1])):
if G[1][node][i] == 1 and G[1][node][i] not in visited:
queue.append(i)
return visited
def idx_to_key(list, N):
keys =[]
for i in list:
keys.append(N[i])
return keys
idxs = BFS_tbl(G1, 5)
print(idxs, idx_to_key(idxs, N1)) # [5, 4, 6, 7, 0, 3, 1, 2] ['v', 'u', 'w', 'x', 'q', 't', 'r', 's']