이진 탐색 트리(BST, binary search tree) 개념과 파이썬 구현, 백준 Binary Search 예제풀이

soyyeong·2023년 10월 8일
1

학교 수업인 산업경영알고리즘 중간고사를 대비하기 위한 기록입니다.

📕 이진탐색트리란?

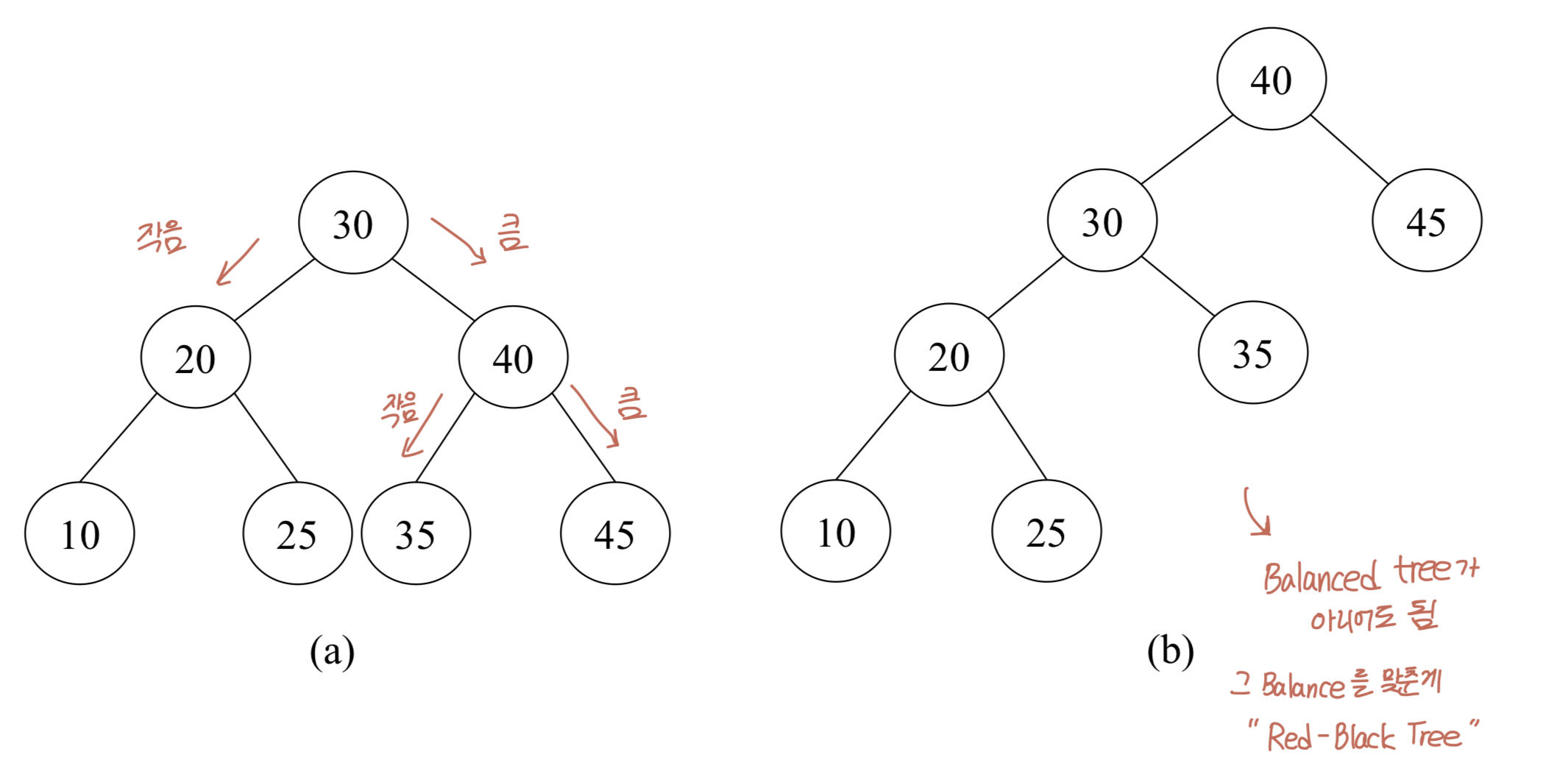
  1. 이진트리다.
  2. 왼쪽 부분트리에 있는 모든 노드는 그 노드의 데이터보다 작아야 한다.
  3. 오른쪽 부분트리에 있는 모든 노드는 그 노드의 데이터보다 커야 한다.

    이진탐색트리는 완전이진트리(Complete Binary Tree)라는 보장은 없다. 따라서 배열이나 파이썬 리스트를 써서 구현하지 않고, 노드 클래스 정의한 후 여러 노드 인스턴스를 생성하고 이 인스턴스를 연결시켜 구현한다.

📗 이진탐색트리 구현

이제 이진탐색트리에서 특정 노드를 검색, 삽입, 삭제 하는 작업을 구현해보자.
코드잇 강의를 들을 때 나왔던 코드와 교재의 코드가 살짝 달라서 둘 다 살펴보자.

ver.1 코드잇

노드 클래스
우선 노드 클래스를 만들어준다. 그 노드의 데이터값과 부모노드, 왼쪽자식, 오른쪽자식을 지정할 수 있다.

class Node:
  """이진 탐색 트리 노드 클래스"""
  def __init__(self, data):
    self.data = data
    self.parent = None
    self.left_child = None
    self.right_child = None

이진탐색트리 클래스
이진탐색트리의 연산들을 수행할 수 있는 클래스도 만들어준다. 루트노드를 설정할 수 있도록 한다.

class BinarySearchTree:
    """이진 탐색 트리 클래스"""
    def __init__(self):
        self.root = None

이진탐색트리 검색
이진탐색트리 클래스에 아래 탐색 메소드를 추가해준다.
찾고 싶은 data를 파라미터로 받는다. 비교하는 노드(compare_node)를 먼저 루트노드부터 설정해서 data와 비교한다.

if 1 ) data < compare_node ➡️ compare_node를 왼쪽자식으로 변경한다.

if 2 ) data > compare_node ➡️ compare_node를 오른쪽자식으로 변경한다.

  • 만약 왼쪽자식이나 오른쪽자식이 없는 경우(None), None을 리턴한다.

if 3 ) data == compare_node ➡️ compare_node를 반환한다.

def search(self, data):
    """이진 탐색 트리 탐색 메소드, 찾는 데이터를 갖는 노드가 없으면 None을 리턴한다"""
    compare_node = self.root
    while True:
      if data < compare_node.data:
        if compare_node.left_child == None:
          return None
        compare_node = compare_node.left_child

      if data > compare_node.data:
        if compare_node.right_child == None:
          return None
        compare_node = compare_node.right_child

      if data == compare_node.data:
        return compare_node

이진탐색트리 삽입
이진탐색트리 클래스에 아래 삽입 메소드를 추가해준다.
넣고싶은 data를 파라미터로 받고, Node class로 새로운 노드(new_node)를 정의한다.

  1. 트리가 비었을 때
    a. new_node를 루트노드로 지정한다

  2. 비교할 노드(compare_node)를 먼저 루트노드로 설정한다.
    a. new_node의 값 < compare_node의 값

    1. compare_node의 왼쪽자식이 없으면
      ➡️ 거기에 new_node를 넣고, new_node의 부모노드는 compare_node로 설정한다. return 으로 while 문 탈출.

    2. compare_node의 왼쪽자식이 있으면
      ➡️ compare_node를 왼쪽자식으로 옮겨준다.

    b. new_node의 값 > compare_node의 값

    1. compare_node의 오른쪽자식이 없으면
      ➡️ 거기에 new_node를 넣고, new_node의 부모노드는 compare_node로 설정한다. return 으로 while 문 탈출.

    2. compare_node의 오른쪽자식이 있으면
      ➡️ compare_node를 오른쪽자식으로 옮겨준다.

def insert(self, data):
    new_node = Node(data)  # 삽입할 데이터를 갖는 새 노드 생성

    # 트리가 비었으면 새로운 노드를 root 노드로 만든다
    if self.root is None:
        self.root = new_node
        return

    compare_node = self.root
    while True:
      if new_node.data < compare_node.data:
        if compare_node.left_child == None:
          compare_node.left_child = new_node
          new_node.parent = compare_node
          return
        compare_node = compare_node.left_child

      if new_node.data > compare_node.data:
        if compare_node.right_child == None:
          compare_node.right_child = new_node
          new_node.parent = compare_node
          return
        compare_node = compare_node.right_child

이진탐색트리 삭제
삭제 연산이 고려할 게 좀 있는데, 세 가지 경우로 나눠서 생각한다.

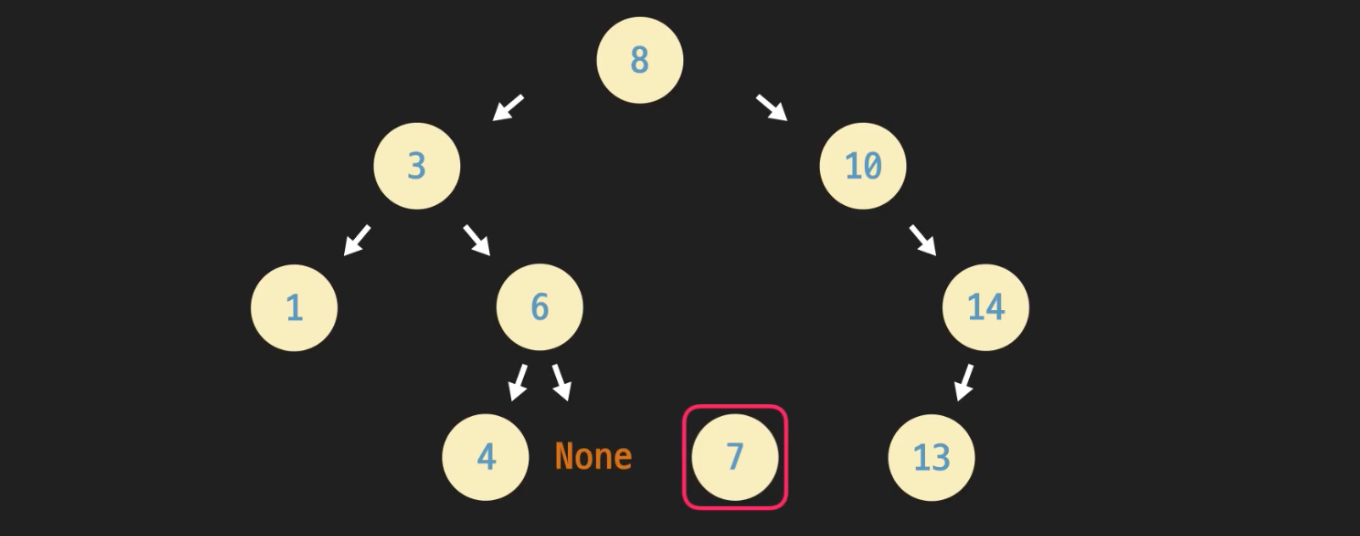
  • 경우1 : leaf 노드 삭제

    • 이런 경우 단순히 leaf 노드의 부모노드를 None으로 지정한다.지우려는 노드가 부모노드의 왼쪽자식인지, 오른쪽자식인지 확인하고 처리해준다.

    • 경우1을 코드로 구현하면 아래와 같다.

def delete(self, data):
    """이진 탐색 트리 삭제 메소드"""
    node_to_delete = self.search(data)  # 삭제할 노드를 가지고 온다
    parent_node = node_to_delete.parent  # 삭제할 노드의 부모 노드

    # 경우 1: 지우려는 노드가 leaf 노드일 때
    if node_to_delete.right_child == None and node_to_delete.left_child == None:
      if node_to_delete.data < parent_node.data:
        parent_node.left_child = None
      elif node_to_delete.data > parent_node.data:
        parent_node.right_child = None
  • 경우2 : 삭제하려는 데이터 노드가 하나의 자식노드를 가질 때
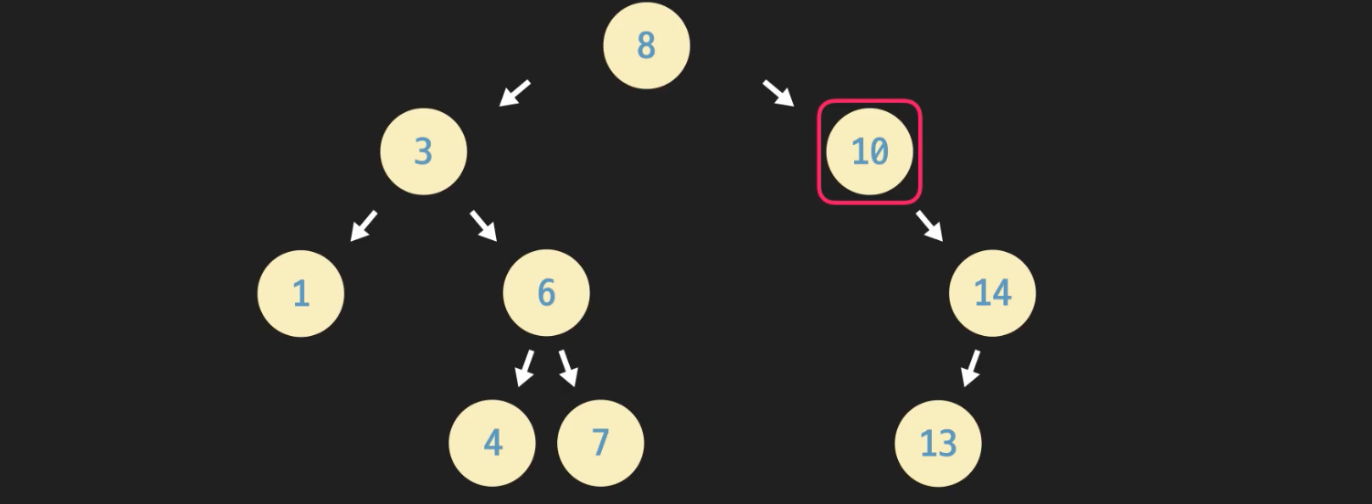
    • 10을 지우고 싶은 경우, 자식노드인 14가 부모 노드의 자리를 차지하면 된다. 그리고 14의 부모노드를 8로 지정한다.
    • 코드로 구현하면 아래와 같다.
# 경우 2: 지우려는 노드가 자식이 하나인 노드일 때:
if parent_node.data > node_to_delete.data:
    if node_to_delete.left_child is None and node_to_delete.right_child is not None:
        parent_node.left_child = node_to_delete.right_child
        node_to_delete.right_child.parent = parent_node
    else:
        parent_node.left_child = node_to_delete.left_child
        node_to_delete.left_child.parent = parent_node
        
else:
    if node_to_delete.left_child is None and node_to_delete.right_child is not None:
        parent_node.left_child = node_to_delete.right_child
        node_to_delete.right_child.parent = parent_node
    else:
        parent_node.left_child = node_to_delete.left_child
        node_to_delete.left_child.parent = parent_node
  • 경우3 : 삭제하려는 데이터의 노드가 두 개의 자식이 있을 때
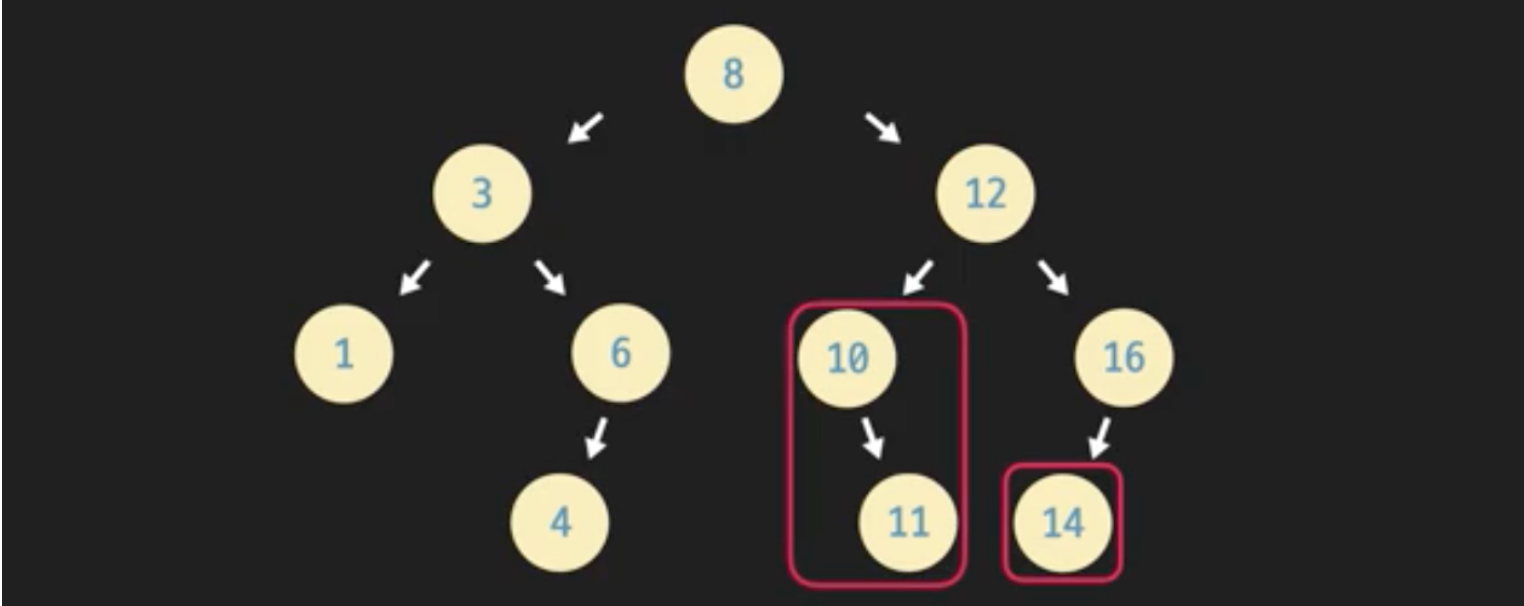
    • 12를 삭제하고 싶은 경우, 14를 12자리로 옮기면 된다.
    • 지우고싶은 노드(12)의 오른쪽 부분트리에서 가장 작은 걸(14) 선택하면 되는데, 이걸 successor라고 부른다.
  • 두 개의 자식이 모두 있는 노드를 삭제하는 경우
    1. 지우려는 successor를 받아온다. (find_min()메소드 활용)
    2. 삭제하려는 노드 데이터에 successor의 데이터를 저장한 다.
    3. successor 노드를 삭제한다.
    • 이때 successor노드가 부모노드의 오른쪽 자식인지, 왼쪽 자식인지,
    • successor 노드가 오른쪽 자식을 가지는지 아닌지를 고려해야 한다.
    • delete() 메소드는 지우려는 데이터 data를 파라미터로 받는다. 그리고 data를 갖는 노드를 트리에서 삭제한다.
# 경우 3: 지우려는 노드가 2개의 자식이 있을 때

else:
  successor = self.find_min(node_to_delete.right_child)

  node_to_delete.data = successor.data

  # successor 노드가 어떤 부모 노드의 왼쪽 자식일 때
  if successor == successor.parent.left_child:
    successor.parent.left_child = successor.right_child
  else: # sucessor 노드가 삭제하려는 노드의 바로 오른쪽 자식일 때
    successor.parent.right_child = successor.right_child

  if successor.right_child is not None: # successor 노드가 오른쪽 자식이 있을 떄
    successor.right_child.parent = successor.parent

(이후 더 추가할 예정)
코드 사용해보기

ver.2 교재 수도코드

검색

삽입

삭제

📘 이진탐색트리 시간복잡도

📙 BOJ 예제풀이

중간고사가 네트워크 차단한 상태로 코딩하는 형식으로 진행된다고 하여 이를 대비하기 위해 코테를 하루에 하나씩 풀 예정이다! 이번 챕터에서는 백준 이분탐색(Binary Search) 문제집 에 있는 문제 두 가지를 꼽아서 풀어보겠다.

1)

2)

+) 기출풀기

profile
soyyeong
이전 포스트

[자료구조] 그래프탐색, BFS, DFS

다음 포스트

Red-Black Tree(RB Tree)의 개념, 삭제 및 삽입 연산 파이썬 구현

0개의 댓글