MONET: Mixture of Monosemantic Experts for Transformers

하임·2025년 2월 2일

MoE

목록 보기
8/9

https://arxiv.org/pdf/2412.04139

MONET: Mixture of Monosemantic Experts for Transformers (요약 및 상세 설명)

논문 제목: MONET: Mixture of Monosemantic Experts for Transformers

저자: Jungwoo Park, Young Jin Ahn, Kee-Eung Kim, Jaewoo Kang

소속: Korea University, KAIST, AIGEN Sciences

1. 연구 동기 및 문제점

  • 대규모 언어 모델(LLM)의 내부 연산 해석 및 투명성 확보의 중요성
  • 폴리세만틱성(polysemanticity): 하나의 뉴런이 여러 비관련된 개념에 반응하는 문제
  • 기존 Sparse Autoencoder(SAE) 방식의 한계
    • 사후 재구성 손실(post-hoc reconstruction loss) 문제
    • LLM 성능 저하
    • 모델의 일반 성능 유지와 해석 가능성 간의 트레이드오프 발생

2. MONET 아키텍처 소개

  • *MONET (Mixture of Monosemantic Experts for Transformers)**는 기존 Mixture-of-Experts(MoE)와 Sparse Dictionary Learning 기법을 결합한 새로운 아키텍처입니다.

주요 기여:

  • 전문가 수 확장: 각 계층당 262,144개의 전문가를 사용
  • 메모리 효율적 전문가 분할: 전체 파라미터 수는 전문가 수의 제곱근에 비례
  • 기계론적 해석 가능성 제공: 전문가 간의 상호 배타적 지식 표현을 보장
  • 지식 조정 및 제어 가능: 독성 콘텐츠 제거, 언어, 도메인별 전문가를 활용한 조정 가능

3. 기존 MoE 기법과 MONET 비교

모델전문가 선택 시간 복잡도메모리 사용량
SMoEO(Nd)O(Nd)O(Nmd)O(Nmd)
PEERO((N+k2)Hd)O((\sqrt{N}+k^2)Hd)O(Nd)O(Nd)
MONETO(NHd)O(\sqrt{N}Hd)O(Nmd)O(\sqrt{N}md)
  • SMoE: 전문가 수 N에 비례하는 복잡성
  • PEER: N의 제곱근 복잡도지만 메모리 사용량이 큼
  • MONET: 제곱근 복잡도를 유지하면서 메모리 사용량 절감

4. MONET의 전문가 분할 방식

4.1 수평 전문가 분할 (Horizontal Decomposition, HD)

  • 전문가를 하위 및 상위 계층으로 분할
  • 메모리 효율성을 위해 N\sqrt{N}개의 전문가만 사용하여 계층을 동적으로 결합

4.2 수직 전문가 분할 (Vertical Decomposition, VD)

  • 각 전문가를 입력 및 출력 계층으로 수직 분할
  • N\sqrt{N}개의 하위 및 상위 계층을 각각 결합하여 메모리 사용량 절감

5. 실험 및 성능 비교

데이터셋 및 모델 크기

  • 모델: 850M, 1.4B, 4.1B 파라미터
  • 벤치마크: MMLU, ARC, PIQA, SIQA, OBQA, HS, CSQA 등

결과 요약 (0-shot 및 5-shot 평가)

  • MONET-VD(수직 분할)가 MONET-HD보다 성능 우수
  • 전문가 수를 확장하면서도 성능 유지
  • SAE에 비해 MONET가 더 나은 해석 가능성을 제공

6. 전문가의 단일 의미성 (Monosemanticity)

  • MONET 전문가들은 특정 개념에만 반응
  • 예시: 전문가 73,329는 "U.S. States"에 특화, 147,040은 "Chemical Compounds"에 특화

7. 추가 분석: 지식 조정 및 제거

7.1 도메인 마스킹 (Domain Masking)

  • 특정 도메인에 대한 전문가를 제거 후 모델 성능 변화 측정
  • 특정 도메인 성능만 감소하고, 다른 도메인 성능은 유지

7.2 다국어 마스킹 (Multilingual Masking)

  • Python, C++, Java 등의 프로그래밍 언어 전문가 제거 후 성능 평가
  • 제거한 언어에 대해서만 성능 하락, 나머지 언어는 유지

7.3 독성 전문가 제거 (Toxic Expert Purging)

  • 독성 콘텐츠 생성과 상관관계가 높은 전문가를 제거
  • REALTOXICITYPROMPTS 및 ToxiGen 벤치마크에서 독성 점수 감소

8. 결론 및 기여

  • MONET는 기존 MoE 아키텍처의 한계를 해결
  • 262,144명 전문가 활용: 더욱 해석 가능한 전문가 구성
  • 효율적 메모리 사용: 제곱근 수준의 메모리 사용량으로 전문가 수 확장
  • 지식 조정 가능: 도메인, 언어, 독성 조정에 효과적

9. 한계 및 향후 연구 방향

  • 전문가 선택 기준(루팅 점수 등)이 단순함
  • 자동화된 해석 기술의 양적 평가 필요
  • 향후 사실 기반 생성이나 지식 주입과 같은 응용 가능성 탐색 예정

📌 GitHub 링크

MONET: Transformer 모델을 위한 Monosemantic Experts의 혼합

저자

  • Jungwoo Park¹,²
  • Young Jin Ahn²
  • Kee-Eung Kim²
  • Jaewoo Kang¹,³

¹ Korea University, ² KAIST, ³ AIGEN Sciences

{jungwoo-park, kangj}@korea.ac.kr

{snoop2head, kekim}@kaist.ac.kr

요약

대규모 언어 모델(LLM)의 내부 연산을 이해하는 것은 모델을 인간의 가치와 정렬시키고 독성 콘텐츠 생성과 같은 바람직하지 않은 행동을 방지하기 위해 매우 중요합니다. 그러나 메커니즘적 해석 가능성(mechanistic interpretability)은 다의성(polyspecificity)에 의해 방해받고 있습니다. 이는 개별 뉴런이 여러 개의 관련 없는 개념에 응답하는 현상을 말합니다.

희소 자동 인코더(SAE, Sparse Autoencoders)는 특징적 사전 학습 방법을 통해 이 문제를 해결하려 시도했지만, 높은 재구성 손실로 인해 모델의 일반화 성능을 저하시키는 문제가 있었습니다.

이를 해결하기 위해 MONET(Mixture of Monosemantic Experts)를 제안합니다. 이는 end-to-end 학습이 가능한 Mixture-of-Experts 구조를 통해 다의성을 해결하고, 각 레이어에서 파라미터를 사전적으로 지식에 따라 전담하는 전문가로 구성된 새로운 메커니즘을 도입합니다.

MONET는 다음과 같은 특징을 가지고 있습니다:

  1. 다양한 도메인 및 언어에서의 조작 가능성을 향상합니다.
  2. 독성 완화를 지원합니다.
  3. 일반적인 성능 향상을 제공합니다.

MONET는 확장 가능한 전문가 네트워크를 통해 효율적으로 매커니즘적 해석 가능성을 제공합니다. 학습된 모델의 코드와 체크포인트는 아래에서 확인할 수 있습니다:

https://github.com/dmis-lab/Monet

1. 도입 (Introduction)

대규모 언어 모델(LLM)은 지속적으로 확장되고 일반화되고 있습니다 (Radford et al., 2019; Brown et al., 2020). 그러나 모델 내부 연산의 메커니즘적 해석 가능성은 LLM을 인간과 정렬시키기 위해 매우 중요합니다 (Bereska & Gurevets, 2024).

메커니즘적 해석 가능성이란 뉴럴 네트워크 내부의 신경 구조를 인간이 이해할 수 있는 구성 요소로 분해함으로써 이를 분석하려는 시도를 의미합니다. 예를 들어, LLM이 독성 콘텐츠를 생성하거나 바람직하지 않은 행동을 유도하는 방식의 이해는 이러한 해석 가능성을 통해 가능해집니다 (Koch et al., 2023).

현재 LLM의 과제

LLM의 가장 주요한 한계 중 하나는 다의성(polyspecificity)입니다. 이는 개별 뉴런이 여러 가지 관련 없는 개념에 응답하는 현상으로, 다의성은 다음과 같은 문제를 유발합니다:

  1. 비효율적인 모델 설계
    • 현재 구조에서는 특정 전문가(Experts)가 특정 개념에만 전담되지 않고, 여러 개념을 섞어 처리해야 합니다.
  2. 희소 전문가 구조의 한계
    • 기존의 희소 LLM은 한정된 수의 전문가를 사용하며, 이로 인해 각 전문가가 다양한 개념을 처리해야 합니다.
    • 예를 들어, sparse LLM들은 약 2,048개의 전문가만 활용하며, 전문가당 한 가지 이상의 개념을 처리하게 됩니다.
  3. 구조적 제약 및 확장성 문제
    • 전문가의 수를 늘리고 확장하려는 기존 시도들은 비용과 복잡성 문제로 실패했습니다.

MONET의 필요성

이를 해결하기 위해 MONET은 다음과 같은 문제를 다룹니다:

  • 전문가를 세분화하여 다의성을 제거하고, 모델의 해석 가능성을 높임.
  • 효율성을 유지하며 성능 저하 없이 다양한 전문가를 동시에 관리.
  • 지식 기반의 제어를 통해 오픈 도메인 및 독성 완화를 지원.

MONET의 주요 기여

MONET는 다음을 목표로 합니다:

  1. 전문가의 확장 가능성: 기존 구조 대비 파라미터 크기의 제약 없이 최대 26만 개 이상의 전문가를 활용 가능.
  2. 고유 전문가 설계: 각 전문가가 오로지 하나의 개념에만 초점을 맞추어 설계.
  3. 성능과 해석 가능성의 동시 강화: 메커니즘적 해석 가능성과 모델 성능 사이의 균형을 최적화.

2. 기초 개념 (Preliminaries)

희소 전문가 혼합(Sparse Mixture-of-Experts, SMoE)

SMoE 모델은 일부 전문가만 활성화하여 효율적으로 용량을 확장합니다. 이는 계산 비용을 줄이는 데 기여하며, 전문가 임베딩을 활용하여 활성화할 전문가를 결정합니다.

숨겨진 표현 벡터 x∈Rdx \in \mathbb{R}^d와 NN개의 전문가 네트워크 {Ei}i=1N\{E_i\}_{i=1}^N가 주어졌을 때, 각 전문가는 다음과 같이 정의됩니다:

Ei(x)=Viσ(Uix)E_i(x) = V_i\sigma(U_i x)

  • Ui∈Rm×dU_i \in \mathbb{R}^{m \times d}와 는 i번째 전문가의 가중치 행렬입니다. Vi∈Rd×mV_i \in \mathbb{R}^{d \times m}
  • σ\sigma는 ReLU 또는 GELU와 같은 활성화 함수입니다.
  • 전문가 임베딩 와 는 top-k 연산을 나타냅니다. {wi}i=1N⊂Rd\{w_i\}_{i=1}^N \subset \mathbb{R}^d TkT_k

SMoE 계층의 출력은 다음과 같이 계산됩니다:

SMoE(x)=∑i∈KgiEi(x)\text{SMoE}(x) = \sum_{i \in K} g_i E_i(x)

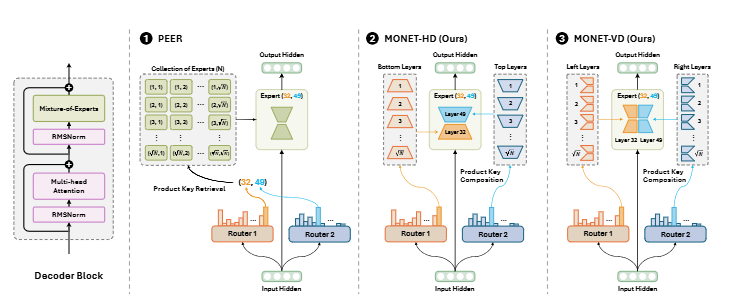
전문가 확장 비교 구조 (Figure 1 설명)

Figure 1에서 대규모 언어 모델에서 전문가 확장을 위한 다양한 구조를 비교합니다.

  1. PEER:
    • 독립적인 전문가를 저장하고 이를 제품으로 검색해 결과를 축적합니다.
    • 메모리 사용량이 전문가 수에 선형적으로 증가 ()합니다. O(N)O(N)
  2. MONET-HD (Horizontal Decomposition):
    • 전문가를 상하단으로 나누어 그룹화하고 이를 동적으로 구성합니다.
    • 복잡도는 로 감소하며, 메모리 사용량은 일정하게 유지됩니다. O(N)O(\sqrt{N})
  3. MONET-VD (Vertical Decomposition):
    • 전문가를 수직적으로 분리하여 각 레이어 내에서 병렬적이고 효율적으로 작업을 수행합니다.
    • O(N)O(N) 복잡도를 유지하면서도 메모리 공간은 효율적으로 사용됩니다.

파라미터 효율적인 전문가 검색 (Parameter Efficient Expert Retrieval, PEER)

PEER는 기존 SMoE 구조보다 효율적으로 동작하며, 계산 복잡도를 N\sqrt{N}으로 줄입니다. 이는 전문가의 임베딩 기반 라우팅 메커니즘을 활용합니다. 이 메커니즘은 (Lamp et al., 2019)를 기반으로 합니다.

PEER의 주요 동작 방식:

각 PEER 전문가는 입력 벡터 x∈Rdx \in \mathbb{R}^d를 처리하기 위해 다중 계층 퍼셉트론(MLP)을 사용하며, 아래와 같은 단계로 구성됩니다:

  1. HH개의 독립적 전문가를 포함.

  2. 각 전문가 임베딩 를 사용하여 를 결정.

    wi,h(1),wi,h(2)∈Rdw{i,h}^{(1)}, w{i,h}^{(2)} \in \mathbb{R}^d

    KhK_h

  3. 이를 통해 Cartesian Product 상에서 상위 전문가를 선택.

    Kh(1,2)K_h^{(1,2)}

수식:

전문가 선택 점수 계산:

Kh=Tk((wi,h(1)x)2+(wi,h(2)x)2)Kh = T_k \left( (w{i,h}^{(1)} x)^2 + (w_{i,h}^{(2)} x)^2 \right)

최종 출력:

PEER(x)=∑h=1H∑j∈Khgh,jEj(x)\text{PEER}(x) = \sum{h=1}^H \sum{j \in Kh} g{h,j} E_j(x)

제약 사항 및 한계

PEER는 계산 복잡도를 크게 줄이지만, 병목 현상(bottleneck) 문제가 발생할 수 있습니다.

  • 예를 들어, 전문가 수가 2048이고 주어진 LLM에 1.3 billion 파라미터가 있는 경우, PEER는 추가적인 103 billion 파라미터를 요구할 수 있습니다.

아래는 제공된 이미지를 기반으로 논문의 세부 내용을 빠짐없이 번역 및 설명한 결과입니다.

3. MONET: Transformer 모델을 위한 Monosemantic Experts의 혼합

목표

LLM의 혼합된(superposed) 특징을 분리하기 위해, MONET은 기존 SMoE 사전 학습 방식을 확장하여 전문가의 수를 극대화하는 것을 목표로 합니다. 독립된 전문가 집합 대신, MONET은 전문가의 제품 키 조합(Product Key Composition) 방식을 도입하여 PEER의 메모리 제한 문제를 해결하고 전문가 네트워크를 효율적으로 구성합니다.

MONET은 두 가지 주요 레이어 분할 방법을 활용합니다:

  1. 수평적 전문가 분해(Horizontal Expert Decomposition, HD)
  2. 수직적 전문가 분해(Vertical Expert Decomposition, VD)

이 방식은 전문가 수를 확장하면서 메모리 병목 현상을 해결하며, 전문가 수의 제곱근 수준에서 파라미터 성장을 유지합니다.

수평적 전문가 분해 (Horizontal Expert Decomposition, HD)

HD는 기존의 독립적인 전문가를 유지하는 대신, 전문가를 상단(top)과 하단(bottom) 레이어로 분리하여 동적으로 상호 작용하도록 설계됩니다. 이를 통해 다음과 같은 방식으로 전문가를 구성합니다:

전문가 구성

Ei,j(x)=Vjσ(Uix+bi(1))+bj(2)E_{i,j}(x) = V_j \sigma(U_i x + b_i^{(1)}) + b_j^{(2)}

여기서:

  • i: 하단 전문가
  • j: 상단 전문가

전문가 계층의 출력은 다음과 같이 계산됩니다:

MoHDE(x)=∑h=1H∑i=1N∑j=1Ngh,i(1)gh,j(2)(Vjσ(Uix+bi(1))+bj(2))\text{MoHDE}(x) = \sum_{h=1}^H \sum_{i=1}^{\sqrt{N}} \sum_{j=1}^{\sqrt{N}} g_{h,i}^{(1)} g_{h,j}^{(2)} \left( V_j \sigma(U_i x + b_i^{(1)}) + b_j^{(2)} \right)

계산 최적화

HD의 구조는 토큰별 계산 병목 현상을 해결하기 위해 전문가 라우팅 점수 gg를 미리 계산하도록 설계되었습니다.

이를 통해 메모리 집약적인 연산을 전문가 라우팅 이전과 이후로 나누어 처리할 수 있습니다.

수직적 전문가 분해 (Vertical Expert Decomposition, VD)

VD는 HD와 직교하는 방식으로 전문가를 수직으로 분리합니다. 이는 전문가 네트워크를 상단(top)과 하단(bottom)으로 분리하는 대신, 세그먼트를 나누어 각 세그먼트에 독립적인 가중치를 할당합니다.

전문가 정의

Eij(x)=Vj(2)σ(Ui(1)x+bi(1))+bj(2)E_{ij}(x) = V_j^{(2)} \sigma\left(U_i^{(1)} x + b_i^{(1)} \right) + b_j^{(2)}

VD의 전문가 계층 출력은 다음과 같이 계산됩니다:

MoVDE(x)=∑h=1H∑i=1N∑j=1Ngh,igh,j(Vj(2)σ(Ui(1)x+bi(1))+bj(2))\text{MoVDE}(x) = \sum_{h=1}^H \sum_{i=1}^{\sqrt{N}} \sum_{j=1}^{\sqrt{N}} g_{h,i} g_{h,j} \left( V_j^{(2)} \sigma(U_i^{(1)} x + b_i^{(1)}) + b_j^{(2)} \right)

VD는 HD와 유사한 방식으로 메모리 집약적 연산을 최적화하며, 세부 구현은 부록 A.3에서 설명됩니다.

적응형 라우팅 및 배치 정규화 (Adaptive Routing with Batch Normalization)

Top-k 정렬의 하드웨어 비효율성을 피하기 위해 Batch Normalization을 활용하여 라우팅 점수를 정규화합니다. 이 방식은 라우팅 효율성을 높이고 훈련 시간 및 메모리 사용량을 줄입니다.

로드 밸런싱 손실 (Load Balancing Loss)

로드 밸런싱 손실은 전문가가 고르게 활용되도록 보장하여 모델 병목 현상을 방지합니다. 이를 위해 다음과 같은 손실 함수를 도입합니다:

  1. 불균형 손실 (Imbalance Loss)

    전문가 라우팅 분포와 균일 분포 간의 Kullback-Leibler (KL) 다이버전스를 계산:

    Lunif=−12HN∑h=1H∑i=1Nlog⁡gh,i(1)−12HN∑h=1H∑j=1Nlog⁡gh,j(2)L_{\text{unif}} = -\frac{1}{2H\sqrt{N}} \sum_{h=1}^H \sum_{i=1}^{\sqrt{N}} \log g_{h,i}^{(1)} - \frac{1}{2H\sqrt{N}} \sum_{h=1}^H \sum_{j=1}^{\sqrt{N}} \log g_{h,j}^{(2)}

  2. 모호성 손실 (Ambiguity Loss)

    특정 전문가가 높은 확신으로 선택되도록 보장:

    Lamb=−12H∑h=1H(1−max⁡gh,i(1))−12H∑h=1H(1−max⁡gh,j(2))L_{\text{amb}} = -\frac{1}{2H} \sum_{h=1}^H \left(1 - \max g_{h,i}^{(1)}\right) - \frac{1}{2H} \sum_{h=1}^H \left(1 - \max g_{h,j}^{(2)}\right)

최종 손실 함수는 다음과 같이 정의됩니다:

L=LLM+λunifLunif+λambLambL = L_{\text{LM}} + \lambda_{\text{unif}} L_{\text{unif}} + \lambda_{\text{amb}} L_{\text{amb}}

여기서 LLML_{\text{LM}}은 언어 모델 손실, λ\lambda는 가중치를 조정하는 하이퍼파라미터입니다.

4. 평가 (Evaluation)

4.2 오픈 도메인 벤치마크 결과 (Open-Ended Benchmark Results)

Table 2에서 제시된 결과는 MONET이 다양한 모델 크기(850M, 1.4B, 4.1B)에서 경쟁력 있는 성능을 유지하고 있음을 보여줍니다. 특히 다음과 같은 점을 강조합니다:

  • 모든 파라미터 규모에서 일관된 성능 상승: MONET은 0-shot과 5-shot 설정 모두에서 일관된 성능을 보여줍니다. 이는 MONET의 설계가 LLM의 확장성을 효과적으로 활용하고 있음을 나타냅니다.
  • 기존 SAE 구조와의 비교: 특히, SAE 기반의 전문가들은 성능 저하를 겪었지만, MONET은 더 나은 성능을 기록하며 LLM의 신뢰성을 유지했습니다.

세부적인 실험

  • Gemma Scope 모델:
    Gemma 2 2B (Fedus et al., 2023)의 SAE 기반 구조를 사용했습니다.
  • MONET의 성능은 SAE와 비교해 구조적 우위를 보여주었으며, 이는 수평적 분해(HD)보다 수직적 분해(VD)가 더 높은 성능을 제공했음을 보여줍니다.

4.3 질적 분석 (Qualitative Results)

Figure 2:

MONET이 활성화한 전문가의 라우팅 점수(Equation 7에 정의됨)를 시각화한 결과를 보여줍니다. 이는 전문가가 특정 개념에 모노세만틱(monosemantic)하게 작동함을 나타냅니다.

  • 파라미터 지식 (Parametric Knowledge): MONET은 LLM의 디코더 블록 내 MLP를 262,144개의 전문가로 분해하여 더욱 세밀하게 학습합니다. 예: 특정 전문가가 화학 화합물이나 물리학 개념에 특화된 모습을 보입니다.
  • 전문가의 모노세만틱 특성 (Expert Monosemanticity): MONET의 전문가들은 동일한 개념을 다양한 맥락에서 안정적으로 인식합니다. 예:
    • 전문가 48,936과 54,136은 "Bay"라는 단어에 반응합니다.
    • 하나는 "지리적 지역(Bay Area)"과 연결되고, 다른 하나는 "추상적 개념"과 연결됩니다.
  • Self-Explained Experts: MONET은 전문가의 해석 가능성을 높이기 위해 자동 해석 기법을 도입했습니다. 예:
    • 전문가 232,717은 "Cartilage(연골)"로, 전문가 51은 "Expertise(전문성)"으로 해석됩니다.

5. 분석 (Analyses)

5.1 도메인 마스킹 (Domain Masking)

MMLU Pro 벤치마크

MMLU Pro (Wang et al., 2024)를 사용하여 질문-답변 작업을 14개의 도메인으로 분류하고, 도메인 특정 지식 제거(unlearning)를 실험했습니다.

  • 전문가 제거 방식: 특정 도메인에서 라우팅 확률이 두 번째로 높은 도메인보다 두 배 이상 높은 경우, 해당 전문가를 해당 도메인에 특화된 것으로 간주합니다.
    • 이 전문가들을 제거하여 14개 도메인에서의 성능 저하를 분석했습니다.
  • 결과 분석: 전문가를 제거한 후 MONET의 성능 감소는 다른 모델(예: SAE, LLaMA)에 비해 최소화되었습니다. 이는 MONET의 전문가가 도메인 간 지식을 독립적으로 캡슐화하고 있음을 보여줍니다.

6. 결론 (Conclusion)

MONET의 기여

MONET은 262,144개의 전문가를 갖춘 SMoE(Sparse Mixture-of-Experts) 아키텍처로, LLM에서 발생하는 다의성(polyspecificity) 문제를 해결하기 위해 설계되었습니다.

  • *희소 사전 학습(sparse dictionary learning)**을 LLM의 사전 학습(end-to-end SMoE pretraining) 과정에 통합하여, 기존 SAE 구조에서의 후처리 재구성 손실(post-hoc reconstruction loss) 문제를 해결했습니다.
  • MONET의 제품 키 조합(product key composition) 접근법은 기존 SMoE 구조의 메모리 제한을 극복하고, 전문가 수를 최대 262,144개로 확장하면서 전체 파라미터 성장을 전문가 수의 제곱근 수준으로 유지하는 데 성공했습니다.

핵심 특징 및 효과

  • 세밀한 전문가 분할(fine-grained specialization): MONET은 모노세만틱 전문가(monosemantic experts)를 통해 서로 배타적인 개념들을 학습합니다. 이는 모델의 해석 가능성을 높이고 다양한 지식 영역에 대한 세밀한 제어를 가능하게 합니다.
  • 지식 조작(manipulation)의 강건성: MONET은 도메인, 언어, 독성 완화와 같은 다양한 영역에서의 지식 조작을 강력히 지원합니다. 이는 모델의 전반적인 성능을 손상시키지 않으면서 이루어졌습니다.
  • 확장 가능성: 전문가의 수를 확장하고 LLM 내에서 모노세만틱 전문화를 촉진함으로써, 모델 해석 가능성과 제어 가능성을 동시에 개선했습니다. MONET의 연구 결과는 미래의 투명하고 정렬된 언어 모델 개발의 길을 열어줍니다.

제한 사항 (Limitations)

  1. 전문가 선택의 편향성:

    라우팅 점수(routing scores)의 편향성이 특정 도메인 전문가를 결정하는 데 영향을 미칠 수 있음을 발견했습니다.

    • 예를 들어, 독성 점수와 라우팅 점수 간의 Pearson 상관 계수를 계산하여 이를 분석했습니다.
    • 하지만, 이러한 편향성은 비교적 최소한의 수준으로 유지되었습니다.

  2. 전문가 선택 방법론의 개선 필요:

    더 정교한 전문가 선택 메커니즘 개발은 향후 연구의 유망한 방향으로 간주됩니다.

  3. 해석 가능성의 한계:

    자동 해석 기법(예: self-explained experts)이 여전히 일부 질문에 대해 모호한 결과를 나타낼 수 있음을 발견했습니다.

    따라서, 파라미터 기반 조작의 응용은 지식 학습과 관련된 문제를 해결하는 데 제한적일 수 있습니다.

미래 연구 방향

MONET의 결과는 LLM이 내재적 지식을 효과적으로 검색하는지 여부, 그리고 SMoE LLM에서 평생 학습(lifelong learning)이 가능한지에 대한 질문을 다루는 데 있어 유망한 연구 방향을 제시합니다.

이를 통해 더 투명하고 신뢰할 수 있는 LLM 개발의 가능성을 열었습니다.

왜 전문가 수를 늘리는 것이 모노세만틱 특성을 강화하는가?

  1. 세분화된 지식 분리 (Fine-grained Specialization):
    • 전문가의 수가 증가하면 각 전문가가 담당하는 지식의 범위가 좁아집니다.
    • 이는 특정 전문가가 한 가지 개념 또는 좁은 범위의 지식에만 특화될 수 있도록 합니다.
    • MONET에서는 최대 262,144개 전문가를 활용함으로써, 각 전문가가 모노세만틱한(즉, 특정한 개념에만 반응하는) 특성을 갖도록 설계되었습니다.
  2. 모호성 감소 (Reduction in Polyspecificity):
    • 기존 LLM 구조에서는 뉴런이나 전문가가 여러 개념에 동시에 반응하는 다의성(polyspecificity) 문제가 있었습니다.
    • 전문가 수를 늘림으로써 이 문제를 완화하고, 각 전문가가 특정 개념에만 집중하도록 유도할 수 있습니다.
  3. 실험적 결과:
    • MONET의 실험에서는 전문가가 증가할수록 단어와 컨텍스트에 대해 더 모노세만틱하게 반응하는 모습을 보여주었습니다.
    • 예를 들어, "Bay"라는 단어에 대해 하나의 전문가는 지리적 의미("Bay Area")에 반응하고, 다른 전문가는 추상적 개념에 반응했습니다. 이는 전문가 수가 충분히 많을 때 가능한 일입니다.

전문가를 나누는 구조(HD/VD)는 효율성을 높이는 역할

반면, MONET에서 전문가를 나누는 구조(HD: 수평적 분해, VD: 수직적 분해)는 주로 계산 효율성을 높이고 메모리 사용량을 줄이는 데 초점이 맞춰져 있습니다.

  • 전문가 수가 증가하면 계산 비용과 메모리 요구량이 급격히 늘어납니다. 이를 해결하기 위해 MONET은 HD와 VD를 사용해 전문가를 효율적으로 분할합니다.
  • 이러한 구조는 전문가 수를 늘리는 것의 부작용(비용 증가)을 완화하지만, 모노세만틱 특성을 직접적으로 만드는 데 기여하지는 않습니다.

결론

  • 모노세만틱 특성은 전문가 수를 늘리는 것에서 기인합니다.
  • HD/VD 같은 전문가 분할 방법은 이러한 모노세만틱 전문가 구조를 효율적으로 유지하기 위한 보조적인 설계라고 이해할 수 있습니다.
  • 따라서 MONET의 핵심은 전문가 수를 대규모로 늘리고 이를 효과적으로 관리하면서도 메모리와 계산 자원을 최적화하는 데 있다고 볼 수 있습니다.
profile
하임
NLP 공부합니당
이전 포스트

OLMoE: Open Mixture-of-Experts Language Models

다음 포스트

Branch-Train-MiX: Mixing Expert LLMs into a Mixture-of-Experts LLM

0개의 댓글