OLMoE: Open Mixture-of-Experts Language Models

하임·2024년 11월 28일

MoE

목록 보기

7/9

https://arxiv.org/pdf/2409.02060

간단 요약

논문 "OLMoE: Open Mixture-of-Experts Language Models"는 Mixture-of-Experts (MoE) 구조를 사용하는 개방형 언어 모델 OLMoE에 대한 연구를 다룹니다.

1. 연구 목표와 배경

문제점: 대형 언어 모델(LLM)은 뛰어난 성능을 제공하지만, 높은 비용으로 인해 학계와 오픈소스 개발자들에게 접근이 제한적임.
해결책: MoE 구조를 활용하여 활성화된 파라미터만 일부 사용함으로써 비용과 성능의 균형을 개선.
기여: 완전한 개방형 MoE 모델인 OLMoE를 소개하고, 모델 가중치, 학습 데이터, 코드, 학습 로그를 모두 공개.

2. 모델 구조와 주요 설계

OLMoE-1B-7B 모델:
- 총 69억 파라미터 중 13억 파라미터만 활성화.
- MoE 모듈: 각 레이어에 64개의 작은 전문가(Experts)를 배치하고, 입력 토큰당 8개의 전문가를 활성화.
- 라우터: Dropless token-based 라우팅 알고리즘 사용.
손실 함수:
- Cross-entropy 손실(LCE) 외에 Load Balancing Loss (LLB)와 Router Z-loss (LRZ)를 추가로 사용해 안정성 및 성능 향상.
주요 설계 선택:
- 전문가의 세분화 (64개 전문가, 8개 활성화).
- 공유 전문가를 사용하지 않음.
- Sparse upcycling을 제외하고 처음부터 MoE 모델 학습.

3. 학습 및 데이터 구성

사전학습 데이터:
- DCLM-Baseline과 Dolma 1.7의 고품질 데이터 조합을 사용.
- 총 5.1조 토큰(약 1.3 epochs) 학습.
적응(adaptation):
- Instruction tuning: 코딩 및 수학 관련 데이터 추가.
- Preference tuning: DPO를 사용해 사용자 선호도 반영.

4. 실험 결과

성능 평가:
- OLMoE-1B-7B는 동일한 활성 파라미터를 사용하는 다른 모델보다 성능이 우수.
- Llama2-7B와 같은 밀집(dense) 모델과 유사한 MMLU 점수를 보임.
- MoE 구조로 인해 학습 속도가 밀집 모델 대비 약 2배 빠름.
하이퍼파라미터 실험:
- 전문가의 세분화, 라우팅 알고리즘, 초기화 방식, QK-Norm 사용 등이 성능에 미치는 영향을 분석.

5. 주요 분석 및 한계

라우팅 특성 분석:
- 라우팅 초기 단계에서 전문가들이 도메인 및 어휘 특화되는 경향을 확인.
- Load Balancing Loss가 전문가의 불균형을 방지하지만, 유연성을 제한할 수 있음.
한계 및 향후 연구:
- MoE의 복잡한 설계 문제 해결이 필요.
- 모델의 안정성을 더 개선하기 위한 실험 제안.

활용 방안

논문은 MoE 구조를 활용한 비용 효율적인 대형 언어 모델 설계에 관심이 있는 연구자들에게 유용하며, OLMoE의 공개 리소스를 활용해 추가 실험 및 확장이 가능합니다.

OLMoE의 구조 및 설계에 대해 논문 내용을 바탕으로 더 자세히 설명.

1. OLMoE의 모델 구조

OLMoE는 Mixture-of-Experts (MoE) 구조를 기반으로 하는 Decoder-Only 언어 모델입니다. 이 구조는 기존 밀집(dense) 모델과 달리, 특정 입력 토큰에 대해서만 일부 파라미터를 활성화하여 효율성을 극대화합니다.

(1) MoE 모듈

구성 요소:
- MoE 모듈은 밀집 모델의 Feed-Forward Network (FFN)를 여러 작은 전문가(experts)로 대체.
- 레이어마다 64개 전문가를 배치하며, 입력 토큰당 8개 전문가 활성화.
작동 원리:
- Router가 각 입력 토큰을 특정 전문가로 라우팅하여 처리.
- 활성화된 전문가들의 출력을 가중합(Weighted Sum)하여 최종 출력 생성.

MoE 모듈:

$\text{MoE module}(x) = \sum_{i=1}^{k} p_i \cdot E_i(x)$
]

x: 입력 토큰 $E_i(x)$ : 선택된 전문가 i의 출력 $p_i$ : 라우팅 확률

(2) 라우팅 알고리즘

OLMoE는 Dropless Token-based Routing을 채택:
- Token-based Routing: 각 토큰이 여러 전문가를 선택. 이 방식은 Expert-based Routing보다 유연.
- Dropless: 모든 토큰이 최소 한 명의 전문가에 할당되도록 보장.
Load Balancing Loss (LLB):
- 라우터가 특정 전문가만 자주 선택하지 않도록 균형을 유지하는 손실 항목 추가.
- 각 전문가의 활성화 빈도를 고려하여 손실 계산.

(3) 손실 함수

OLMoE의 최종 손실 함수는 다음과 같습니다:

$L = L_{CE} + \alpha \cdot L_{LB} + \beta \cdot L_{RZ}$

$L_{CE}$ : Cross-Entropy Loss (기본 손실).
$L_{LB}$ : Load Balancing Loss (라우팅 균형 유지).
$L_{RZ}$ : Router Z-Loss (라우팅 안정성 확보).
$\alpha$ , $\beta$ : 각 손실의 가중치 (논문에서는 0.01, 0.001 사용).

2. 주요 설계 선택

OLMoE는 다양한 설계 선택을 통해 효율성을 높이고 안정성을 확보했습니다.

(1) 활성 파라미터 및 총 파라미터

활성 파라미터: 13억(1.3B)개로 제한해 추론 비용을 최소화.
총 파라미터: 69억(6.9B)개로 높은 표현력 유지.

(2) 전문가의 세분화 (Expert Granularity)

설계 선택:
- 전문가를 작게 나누어 총 64개의 전문가 배치.
- 레이어당 활성화된 전문가 8개로 구성.
- 세분화 장점:
  - 더 다양한 전문가 조합 가능 (조합 수: > 40억). (648)\binom{64}{8}
  - 특정 입력 데이터에 더 세밀하게 특화 가능.

(3) 공유 전문가 배제 (No Shared Experts)

공유 전문가(항상 활성화되는 전문가)는 모델의 유연성을 제한하므로 사용하지 않음.
대신, 특정 전문가가 자주 활성화되도록 모델이 학습 과정에서 스스로 결정.

(4) Sparse Upcycling 미사용

밀집 모델을 MoE로 변환하는 Sparse Upcycling 방식을 사용하지 않고 처음부터 MoE로 학습.
- 이유: 밀집 모델의 설계 제약으로 인해 최적의 성능을 내기 어려움.

(5) QK-Norm 활용

Query-Key 프로젝션 후 추가적인 정규화를 통해 안정성을 강화.

3. 모델 학습 및 데이터

학습 데이터:
- DCLM-Baseline, Dolma 1.7 데이터 혼합.
- 총 5.1조 토큰 학습.
학습 방법:
- RMSNorm 사용으로 안정성 확보.
- 모든 파라미터(임베딩 포함)에 가중치 감쇠(Weight Decay) 적용.

4. OLMoE와 밀집 모델 비교

MoE의 주요 장점:
- 활성화된 파라미터만 사용하므로 추론 비용이 낮음.
- 동일한 활성 파라미터를 사용하는 밀집 모델보다 학습이 빠름(약 2배).
밀집 모델 대비 라우팅 안정성 및 도메인 특화 가능성이 높음.

Abstract (요약문)

우리는 희소 Mixture-of-Experts (MoE)을 활용한 완전 개방형, 최신 언어 모델 OLMoE를 소개합니다. OLMoE-1B-7B는 총 70억 개의 파라미터를 가지고 있으며, 입력 토큰당 10억 개의 파라미터만 사용합니다. 이 모델은 5조 개의 토큰으로 사전 학습되었으며, 추가적으로 적응 학습을 통해 OLMoE-1B-7B-INSTRUCT 모델로 발전되었습니다. 우리의 모델은 활성화된 파라미터 수가 비슷한 다른 모델들을 능가하며, Llama2-13B-Chat 및 DeepSeekMoE-16B와 같은 더 큰 모델들보다도 더 나은 성능을 보였습니다. 우리는 MoE 학습에 대한 다양한 실험을 수행하고, 모델 내 라우팅 특성을 분석하며 높은 전문화 수준을 확인했습니다. 또한 모델 가중치, 학습 데이터, 코드, 로그를 포함한 모든 작업을 오픈소스로 공개하였습니다.

1. Introduction (서론)

배경

대형 언어 모델(LLM)은 다양한 작업에서 큰 발전을 이루었지만, 학습과 추론 과정에서 성능과 비용 간의 명확한 트레이드오프가 존재합니다. 성능이 우수한 LLM은 구축 및 배포 비용이 지나치게 높아, 많은 학계 연구자와 오픈소스 개발자들에게 접근 불가능합니다.

희소하게 활성화된 Mixture-of-Experts(MoE) 구조는 이러한 비용-성능 트레이드오프를 개선할 수 있는 하나의 접근 방식입니다. MoE는 각 레이어에 여러 전문가(Experts)를 배치하고, 일부 전문가만 활성화하기 때문에 밀집(dense) 모델에 비해 훨씬 효율적입니다. 이러한 이유로 Gemini-1.5 및 GPT-4와 같은 최첨단 모델들이 MoE를 사용합니다.

문제점

그러나 대부분의 MoE 모델은 폐쇄형입니다. 몇몇은 공개된 모델 가중치를 제공하지만, 학습 데이터, 코드, 또는 학습 방식에 대한 정보는 거의 제공하지 않습니다. MoE 모델은 복잡한 설계 결정(예: 총 파라미터와 활성화된 파라미터의 비율, 전문가의 크기와 수, 공유 전문가의 사용 여부, 라우팅 알고리즘의 선택)을 필요로 하며, 이를 위한 개방형 자원의 부족은 저비용 MoE 모델의 발전을 제한합니다.

기여

이 문제를 해결하기 위해, 우리는 완전 개방형 Mixture-of-Experts 언어 모델 OLMoE를 소개합니다.

OLMoE-1B-7B는 총 69억 개의 파라미터 중, 입력 토큰당 13억 개의 파라미터만 활성화됩니다.
이는 밀집 모델(예: OLMo-1B, TinyLlama-1B)과 유사한 추론 비용을 요구하지만, 69억 개의 총 파라미터를 저장하기 위해 더 많은 GPU 메모리가 필요합니다.
우리의 실험에 따르면, MoE는 활성 파라미터가 동일한 밀집 모델보다 약 2배 더 빠르게 학습됩니다.
OLMoE-1B-7B는 Llama2-13B와 같이 비용이 약 10배 더 많이 드는 모델과 유사한 성능(MMLU 점수)을 보여줍니다.
추가적인 Instruction tuning 및 Preference tuning을 통해 OLMoE-1B-7B-INSTRUCT를 생성하였으며, 이 모델은 Llama2-13B-Chat, OLMo-7B-Instruct, DeepSeekMoE-16B와 같은 더 큰 모델들을 여러 벤치마크(MMLU, GSM8k, HumanEval 등)에서 능가했습니다.

핵심 설계와 분석

MoE의 성능을 높이기 위해 세분화된 전문가와 정밀한 라우팅(fine-grained routing)을 사용:
- 각 레이어에 64개의 작은 전문가 배치.
- 입력 토큰당 8개의 전문가 활성화.
Dropless Token-based Routing 알고리즘이 Expert-based Routing보다 우수함을 확인.
기존 연구와 달리, 공유 전문가(shared experts)가 비효율적이라는 점과, Dense LM에서 MoE로의 Sparse Upcycling이 제한적인 상황에서만 유용함을 발견.
라우팅 분석 결과:
- 사전 학습 초기 단계에서 라우팅이 포화(saturation) 상태에 이르며, 전문가 간의 동시 활성화는 드뭄.
- 전문가들은 도메인 및 어휘 특화(domain and vocabulary specialization)를 보임.

오픈소스화

우리는 MoE에 대한 더 많은 연구와 분석을 촉진하기 위해 다음을 공개합니다:

학습 코드
중간 체크포인트(5000 스텝마다)
학습 로그
학습 데이터
(라이선스: Apache 2.0 또는 ODC-By 1.0)

2. Pretraining and Adaptation (사전 학습 및 적응 학습)

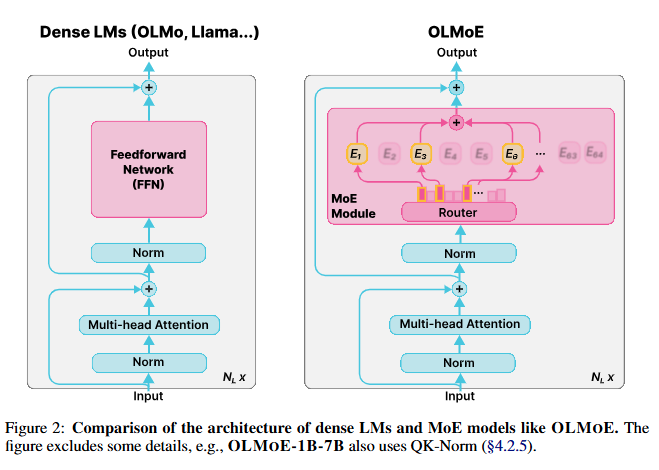
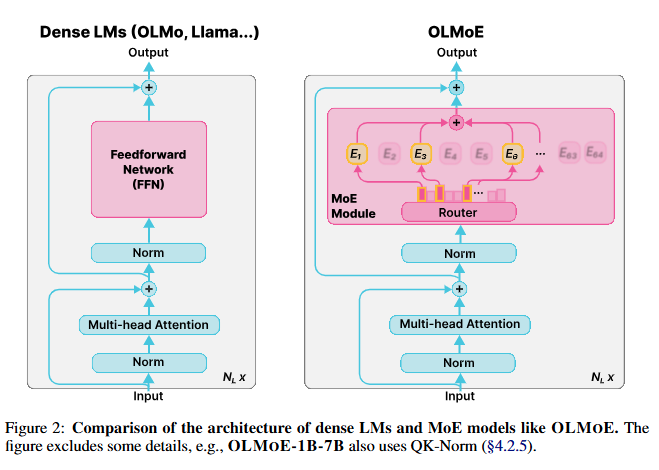
Pretraining Architecture (사전 학습 아키텍처)

OLMoE 모델 구조:
- OLMoE는 디코더 전용(Decoder-only) 언어 모델로, $N_L$ 개의 Transformer 레이어로 구성됩니다.
- 밀집(dense) 모델에서 사용되는 Feedforward Network (FFN) 대신, Mixture-of-Experts (MoE) 모듈로 대체.
MoE 모듈:
- 구성: $N_E$ 개의 작은 FFN 모듈(전문가)로 구성.
- 활성화: 각 입력 토큰 x에 대해 선택된 상위 k개의 전문가만 활성화.
- 작동 원리:
  - 라우터 r(x)는 입력 logits를 r(x)개의 전문가로 매핑하는 학습된 선형 레이어.
  - 각 전문가의 라우팅 확률을 계산하기 위해 softmax를 적용.
  - 활성화된 전문가의 출력은 각자의 라우팅 확률로 가중합하여 최종 출력을 생성.

$\text{MoE module}(x) = \sum_{i=1}^{\text{Top-}k(r(x))} \text{softmax}(r(x))_i E_i(x)$

$r(x)$ : 라우터, $E_i(x)$ : 선택된 전문가의 출력, $\text{softmax}(r(x))_i$ : 라우팅 확률.

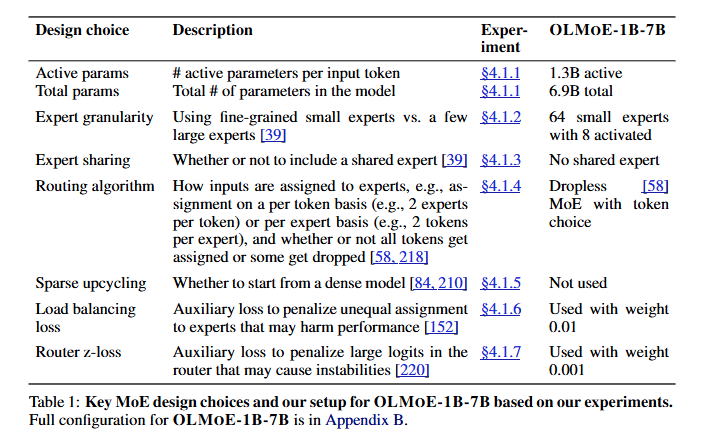
주요 설계 선택

활성 파라미터: 총 69억(6.9B)개의 파라미터 중, 입력 토큰당 13억(1.3B) 파라미터만 활성화.
전문가 수: 레이어당 64개의 전문가 중 8개를 활성화.
라우팅 알고리즘: Dropless Token-based Routing 사용.
- 각 입력 토큰은 라우터 네트워크에 의해 8개의 전문가로 분배.

Loss 구성

OLMoE의 학습 손실 함수는 다음과 같이 정의됩니다:

$L = L_{CE} + \alpha L_{LB} + \beta L_{RZ}$

$L_{CE}$ : Cross-Entropy Loss (기본 손실).
$L_{LB}$ : Load Balancing Loss (라우팅 균형 유지).
$L_{RZ}$ : Router Z-Loss (라우팅 안정성 확보).
$\alpha$ , $\beta$ : 각각의 손실 가중치 ( $\alpha = 0.01$ , $\beta = 0.001$ ).

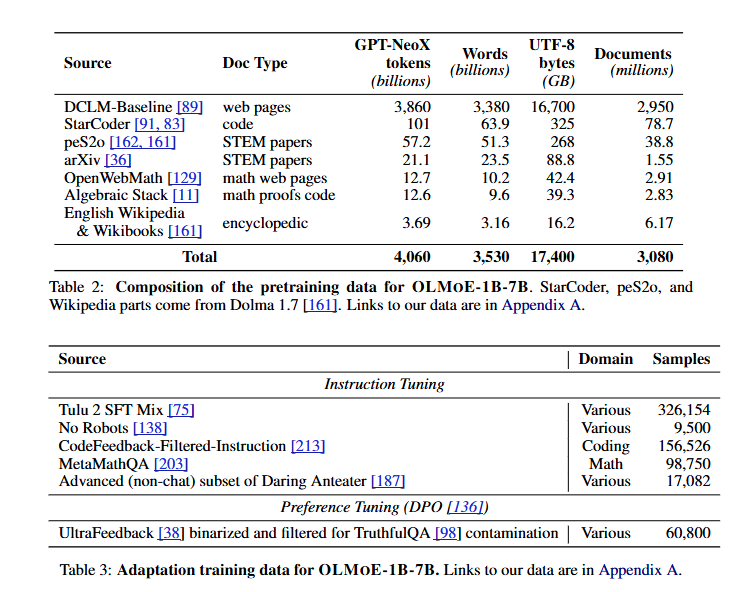
Pretraining Data (사전 학습 데이터)

데이터 소스:
1. Common Crawl에서 품질 필터링된 데이터: DCLM-Baseline
2. StarCoder, Algebraic Stack, arXiv (DCLM 및 Dolma 1.7에 포함).
3. Dolma 1.7에서 가져온 peS2o와 Wikipedia.
데이터 필터링:
- 동일한 n-gram(1~13개의 토큰 범위) 반복이 32회 이상 나타나는 문서를 제거.
- StarCoder 데이터:
  - GitHub에서 별점 2개 미만의 저장소에 속한 문서 제거.
  - 특정 단어가 문서 내에서 30% 이상 반복될 경우 제거.
  - 상위 두 단어의 빈도가 50%를 초과하는 문서 제거.
학습 데이터 통계:
- 총 5.133조(5.1T) 토큰 학습 (1.3 epochs).
- 마지막 100B 토큰의 학습에서는 학습률을 0으로 선형 감소(linear decay).

Adaptation (적응 학습)

OLMoE-1B-7B-INSTRUCT 생성 과정:
1. Instruction Tuning:
  - 코딩 및 수학 데이터를 추가하여 코딩 및 수학 관련 작업 성능 향상.
2. Preference Tuning:
  - 사용자의 선호도를 반영하기 위해 DPO(Direct Preference Optimization) 적용.
사용 데이터:
- Instruction Tuning:
  - 다양한 작업에서 고품질 데이터를 활용 (예: No Robots, Daring Anteater).
  - 코드와 수학 데이터를 추가하여 응용 분야 성능 강화.
- Preference Tuning:
  - TruthfulQA와 같은 평가 벤치마크를 기반으로 이진화 및 필터링된 데이터 사용.

3. Results (결과)

OLMoE-1B-7B의 성능 평가 절차는 다음 세 가지 단계로 나뉩니다:

사전 학습 중 (During Pretraining)
사전 학습 후 (After Pretraining)
적응 학습 후 (After Adaptation)

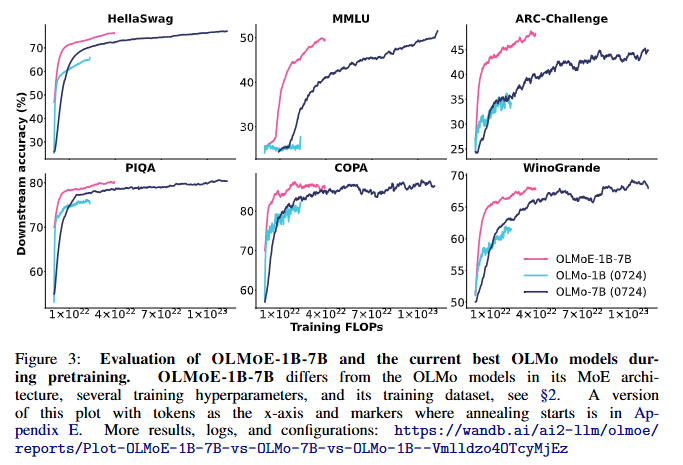
1. 사전 학습 중 (During Pretraining)

평가 방법:
- OLMoE-1B-7B는 학습 중 가장 우수한 기존 OLMo 모델들과 비교 평가되었음.
- 여러 다운스트림 작업에서의 성능을 기준으로 FLOPs(연산량) 대비 성능을 분석.
결과:
- OLMoE-1B-7B는 동일한 작업에서 밀집(dense) 모델인 OLMo 모델보다 적은 연산량(FLOPs)으로 더 나은 성능을 기록.
- 학습 종료 시점에서는, OLMoE-1B-7B가 OLMo-7B와 동일하거나 더 나은 성능을 보였으며, 이는 OLMoE-1B-7B가 OLMo-7B 대비 절반 이하의 FLOPs만 사용한 결과임.
- 이러한 성능 향상은:
  - 데이터셋 조정
  - 모델 구조 변경(MoE 기반 설계 포함)
  - 안정성 및 성능 개선 때문임.
추가 사항:
- 5T 토큰의 사전 학습 동안, 훈련 및 검증 손실 곡선은 매끄럽게 유지되었으며, 주요한 손실 스파이크는 관찰되지 않음(Appendix E 참조).

2. 사전 학습 후 (After Pretraining)

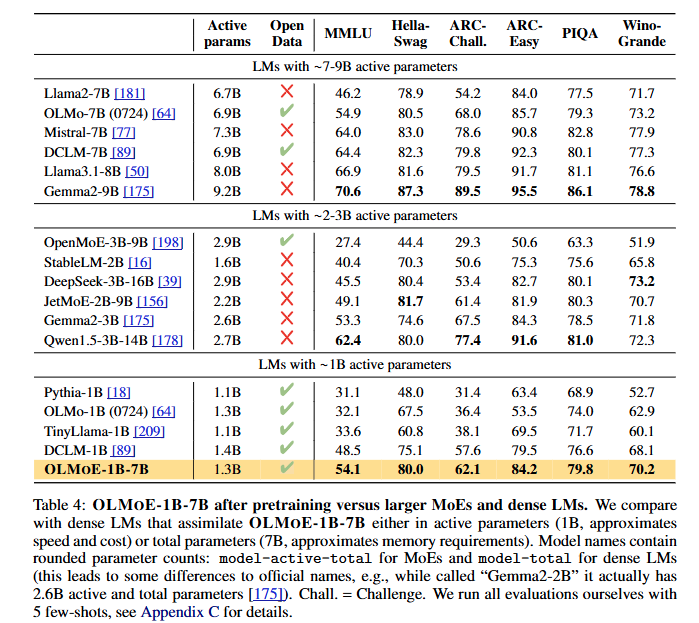
평가 방법:
- Table 4에 제시된 다운스트림 작업에서의 성능을 기반으로 비교.
- 활성 파라미터가 2B 미만인 모델들과 성능 및 효율성을 비교.
결과:
- OLMoE-1B-7B는 활성 파라미터가 2B 미만인 모델들 중 최고 성능을 기록.
- 추론 단계에서 6-7배 적은 연산량만 필요함에도 불구하고, 7B 파라미터를 사용하는 밀집 모델(Llama2-7B)을 일부 작업에서 능가.
- 다만, Llama3.1-8B와 같은 일부 더 큰 모델에는 미치지 못함.
비용 대비 성능 비교:
- Figure 1은 MMLU 점수와 활성 파라미터 수를 기준으로 비용 대비 모델의 가치를 보여줌.
- OLMoE-1B-7B는 비용 효율 측면에서 동급 모델 중 최고 수준.

3. 적응 학습 후 (After Adaptation)

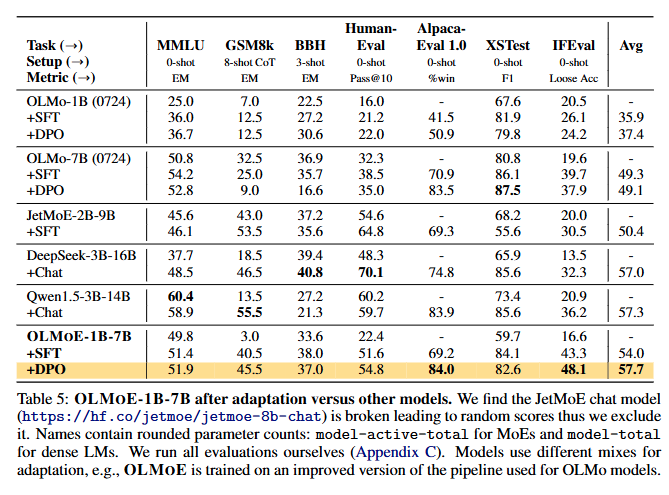
평가 방법:
- Table 5에 제시된 Instruction Tuning(SFT) 및 Preference Tuning(DPO) 적용 후 성능 분석.
- 다양한 벤치마크(MMLU, GSM8k, AlpacaEval 등)를 기준으로 평가.
결과:
- Instruction Tuning (SFT):
  - 모든 평가 작업에서 성능 향상.
  - 특히, GSM8k에서 사전 학습 시 사용된 적은 수학 데이터량을 보완하여 10배 이상의 성능 향상.
- Preference Tuning (DPO):
  - 대부분의 작업에서 추가적인 성능 향상.
  - 특히, AlpacaEval에서 높은 성능을 기록하며, 이는 선행 연구 결과와 일치.
  - DPO 적용된 모델(OLMoE-1B-7B-INSTRUCT)은 모든 벤치마크 모델 중 평균 성능이 가장 높음.
비교 분석:
- OLMoE-1B-7B-INSTRUCT는 Qwen1.5-3B-14B의 Chat 버전을 능가.
- Qwen은 OLMoE-1B-7B보다 2배 이상의 파라미터를 가지고 있음에도 불구하고, OLMoE-1B-7B-INSTRUCT가 더 나은 성능을 기록.
- AlpacaEval 84% 점수는 Llama2-13B-Chat과 같은 더 큰 밀집 모델보다도 높은 성능을 기록.

4. Experimenting with Alternative Design Choices (대체 설계 선택 실험)

이 섹션에서는 OLMoE-1B-7B의 사전 학습 및 적응 학습 실험 결과를 설명합니다. 실험은 다음 세 가지 범주로 나뉩니다:

MoE에 특화된 설정 실험 (§4.1)
밀집 모델과 MoE 모두에 적용 가능한 설정 실험 (§4.2)
적응 학습 실험 (§4.3)

4.1 MoE-specific Pretraining Settings (MoE 특화 사전 학습 설정)

4.1.1 Mixture-of-Experts vs. Dense Models (MoE와 밀집 모델 비교)

배경:
- 이전 연구에서 MoE 모델이 밀집 모델 대비 2~4배 적은 연산량(FLOPs)으로 동등한 성능을 기록함을 보고.
- Switch Transformer와 같은 모델은 2~7배 더 빠른 학습 속도를 달성했지만, 이는 Encoder-Decoder 구조였으며 본 연구는 Decoder-Only 모델에 초점을 둠.
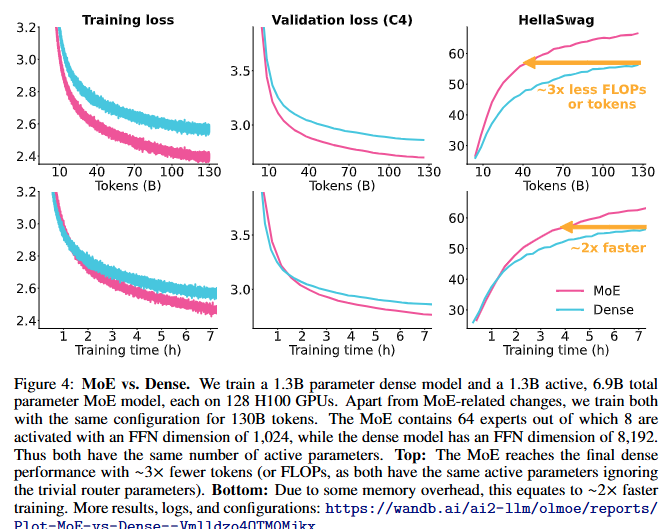
실험 결과:
- Figure 4에 따르면, MoE 모델은 밀집 모델과 동일한 성능을 3배 적은 토큰(약 3배 적은 FLOPs)으로 달성.
- 그러나 MoE의 총 파라미터로 인한 메모리 오버헤드 때문에, GPU당 처리 속도는 밀집 모델보다 느림 (MoE: 23,600 tokens/sec, Dense: 37,500 tokens/sec).
- 학습 시간 기준, MoE 모델이 밀집 모델의 성능에 도달하는 속도는 약 2배 더 빠름.
결론:
- MoE는 비용 효율적이며, OLMoE-1B-7B는 총 69억 개 파라미터와 13억 개 활성 파라미터 구성을 선택.

4.1.2 Expert Granularity (전문가 세분화)

아이디어:
- 작은 크기의 전문가를 더 많이 배치하여 전문가 조합 가능성을 증가시키고 모델의 유연성을 향상.
실험 설계:
- 전문가 수를 8개(활성화 전문가 2개)에서 16개(활성화 전문가 4개)로 늘림으로써, 조합 가능성을 에서 으로 증가.
- $(8 \, C \, 2)$ = 28 $(16 \, C \, 4)$ = 1,820
- 전문가 크기를 줄이면서 더 많은 전문가를 추가해 동일한 연산량을 유지.
결과:
- Figure 5에 따르면, 전문가 수를 증가시키면 학습 손실, 검증 손실, 다운스트림 성능 모두 개선.
- 전문가를 64개(활성화 8개)로 늘릴 경우, 조합 가능성은 로 증가. $(64 \, C \, 8)$ = 4,426,165,368
- 그러나 이 경우 성능 향상은 미미 (1~2%)하며, 세분화의 한계 수익 체감이 나타남.
결론:
- 64명의 전문가를 사용한 OLMoE-1B-7B 설정을 채택.

4.1.3 Shared Experts (공유 전문가)

아이디어:
- 항상 활성화되는 공유 전문가를 추가하여 공통 정보를 학습하도록 유도.
- 이는 중복을 줄이고 다른 전문가들이 더 전문화된 지식을 학습하도록 돕는 것을 목표로 함.
실험 결과:
- Figure 6에 따르면, 공유 전문가를 추가한 설정은 유사한 성능을 보였으나, 오히려 공유 전문가가 없는 설정보다 성능이 소폭 하락.
- 이는 공유 전문가가 모델의 유연성을 제한하기 때문으로 분석됨.
- 공유 전문가를 추가하면 조합 가능성이 에서 로 급감(약 90% 감소). (32 C 4)=35,960(32 \, C \, 4) = 35,960 (31 C 3)=4,495(31 \, C \, 3) = 4,495
결론:
- OLMoE-1B-7B에서는 공유 전문가를 사용하지 않음.
- 공유 전문가의 잠재적 이점은 모델이 스스로 학습하게 두는 것이 더 효과적이라고 판단.

4.1.4 Auxiliary Losses (보조 손실)

손실 항목:
1. Load Balancing Loss (LLB):
  - 토큰이 전문가들 간 고르게 분배되도록 유도.
2. Router Z-Loss (LRZ):
  - 라우팅 안정성 유지.
3. Cross-Entropy Loss (LCE):
  - 기본 손실 함수.
최종 손실:

$L = L_{CE} + \alpha L_{LB} + \beta L_{RZ}$

Expert Choice (EC)와 Token Choice (TC) 비교

Expert Choice (EC):
- 작동 원리: 각 전문가가 입력 시퀀스에서 고정된 수의 토큰을 선택해 처리.
- 장점:
  - 모든 전문가가 같은 수의 토큰을 처리하므로 완벽한 부하 균형(load balance)을 달성.
  - 부하 균형 손실 (Load Balancing Loss, LLB) 없이도 학습 효율 향상.
- 단점:
  - Auto-Regressive Generation에 적합하지 않음. 단일 토큰을 순차적으로 처리하기 때문.
  - 일부 토큰이 선택되지 않아 토큰 누락(Token Dropping)이 발생할 수 있음.
  - 일부 토큰은 여러 전문가에 의해 중복 처리될 수 있음.
Token Choice (TC):
- 작동 원리: 각 토큰이 고정된 수의 전문가를 선택.
- 장점:
  - Auto-Regressive Generation에 적합.
- 단점:
  - 많은 토큰이 동일한 전문가를 선택하면 훈련 효율이 저하될 수 있음.
  - 부하 균형 유지를 위해 LLB 손실을 필요로 함.

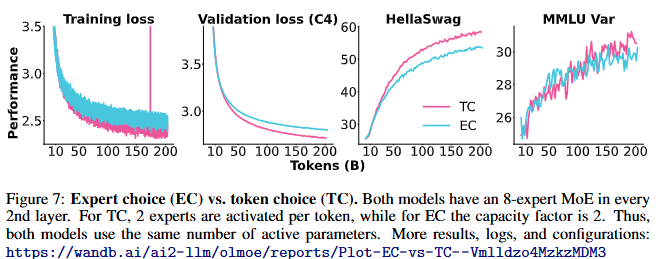
비교 실험 결과 (Figure 7)

성능:
- 동일한 토큰 수 기준으로 TC가 EC보다 더 높은 성능을 보임.
- PIQA, SciQ 등 여러 작업에서 TC의 우월한 성능이 확인됨.
효율성:
- EC는 훈련 속도가 약 20% 빠름:
  - EC: 29,400 tokens/sec
  - TC: 24,400 tokens/sec
결론:
- 텍스트 기반 모델에서는 TC를 선택.
- EC는 이미지 토큰처럼 노이즈가 많은 입력에서 더 적합할 수 있음(멀티모달 모델에서 사용 가능성).

4.1.5 Sparse Upcycling

Sparse Upcycling이란?

목적: 밀집 모델을 MoE 모델로 전환하여 기존 모델 학습의 효율성을 극대화.
절차:
1. 밀집 MLP를 복제하여 각 전문가로 구성.
2. 각 MoE 레이어 앞에 라우터를 새로 추가.
3. 모델을 추가 학습해 전문가들이 특정 데이터에 특화되도록 조정.

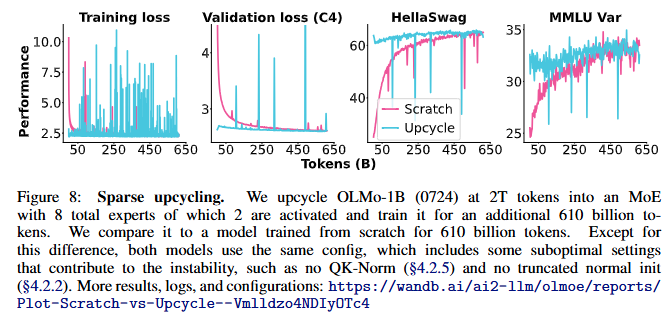
OLMoE 실험 결과 (Figure 8)

비교 모델:
- Sparse Upcycling된 OLMo-1B (0724) 모델.
- 처음부터 MoE로 학습한 모델.
결과:
- 500B 토큰 학습 후, MoE 모델이 Sparse Upcycling 모델의 성능을 따라잡음.
- 600B 토큰에서 MoE 모델이 Sparse Upcycling 모델을 능가.
- Sparse Upcycling의 효율성은 약 25% 수준에 그침(이전 연구의 120% 대비).
제한점:
- Sparse Upcycling 모델은 밀집 모델의 하이퍼파라미터에 제약을 받음:
  - QK-Norm 미사용, 초기화 방식 제한 등이 안정성을 저해.
결론:
- OLMoE-1B-7B에서는 Sparse Upcycling을 사용하지 않음.

4.1.6 Load Balancing Loss (LLB)

LLB의 역할

목적: 특정 전문가로 토큰이 과도하게 치우치는 것을 방지.
계산식:

$LLB = \frac{1}{N_E} \cdot \sum_{i=1}^{N_E} f_i \cdot P_i$

$N_E$ : 전문가 수.
$f_i$ : 전문가 $E_i$ 로 라우팅된 토큰 비율.
$P_i$ : $E_i$ 에 할당된 총 라우팅 확률.

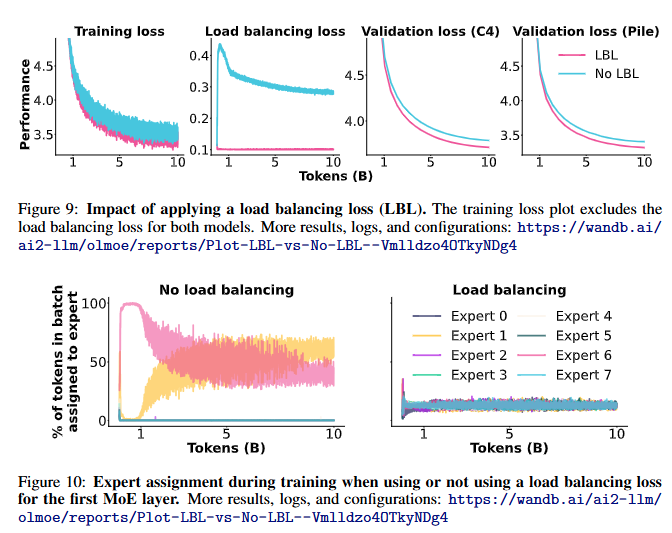
실험 결과 (Figure 9, Figure 10)

손실 곡선:
- LLB 사용 시, 학습 및 검증 손실 모두 개선.
- LLB 미사용 시, 초기에는 특정 전문가에 토큰이 몰리지만, 시간이 지남에 따라 완화.
- 그러나 대부분의 전문가가 비활성(dead weights) 상태로 남아 비효율적.
결론:
- OLMoE-1B-7B는 LLB를 사용(가중치 $\alpha = 0.01$ ).
- 그러나 LLB는 전문가 간의 유연성을 제한할 수 있으며, 이는 향후 연구의 중요한 방향으로 남음.

4.1.7 Router Z-loss

Router Z-loss란?

제안자: Zoph et al. [220]
목적: MoE 모델의 안정성과 품질을 개선.
작동 원리:
- 게이팅 네트워크로 들어오는 큰 logits을 패널티로 처리.
- 큰 logits은 MoE 레이어에서 대규모 행렬 곱셈 시 수치적 오버플로우를 초래할 수 있음.
- 이를 방지하기 위해, 라우터 레이어 바로 직전의 logits $x_j$ 를 지수화하고, 전문가 수 $N_E$ 와 배치 크기 B를 기준으로 평균화하여 손실을 계산.

$L_{RZ}(x) = \frac{1}{B} \sum_{i=1}^B \left( \log \sum_{j=1}^{N_E} \exp(x_j^{(i)}) \right)^2$

가중치:
- 손실에 $\beta$ 라는 가중치를 곱하여 손실 크기를 조정 ( $\beta = 0.001$ , Zoph et al. [220]에 따라 설정).
- 본 연구에서는 $\beta$ 값을 변경하지 않음.

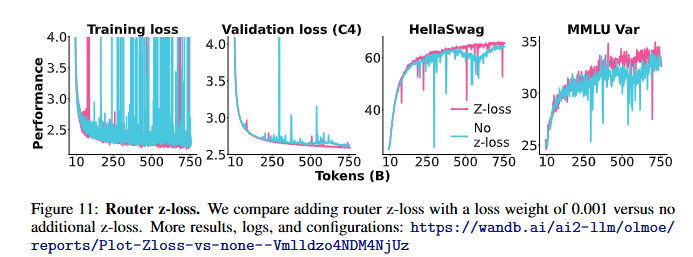
실험 결과 (Figure 11)

성능 및 안정성:
- Router Z-loss를 추가하면 학습 손실, 검증 손실, 다운스트림 성능 모두 향상.
- 학습 안정성이 개선되며 손실 스파이크가 감소.
- 다운스트림 작업에서 높은 성능을 기록.
효율성:
- Router Z-loss를 사용하면 학습 처리량이 약 2% 감소.
- 하지만 품질과 안정성의 개선이 더 중요하다고 판단하여 OLMOE-1B-7B에 적용.
결론:
- OLMOE-1B-7B에서는 Router Z-loss를 $\beta = 0.001$ 로 사용.

4.2 General Pretraining Settings

4.2.1 Dataset Experiments

DCLM-Baseline과 Dolma 1.7의 비교:
- DCLM-Baseline:
  - MMLU 및 기타 벤치마크에서 Dolma 1.7보다 우수한 성능을 기록 (Li et al. [89]).
  - MMLU 및 다운스트림 성능을 목표로 한 데이터셋 분석 결과물이 포함됨.
- OLMOE-MIX:
  - DCLM-Baseline과 Dolma 1.7의 고품질 요소를 혼합하여 구성된 데이터셋.
  - Figure 12에 따르면, OLMOE-MIX는 MMLU를 포함한 모든 다운스트림 작업에서 명확한 성능 향상을 제공.
추가 실험:
- Reddit 및 FLAN 데이터를 추가했지만, 일관된 성능 향상은 발견되지 않음.
- 데이터셋 혼합에 대한 자동화된 접근 방식이 향후 개선 방향으로 제안됨.
결론:
- OLMOE-MIX 데이터셋을 사용해 OLMOE-1B-7B를 사전 학습.

4.2.2 Initialization (초기화)

기존 연구:
- Mixture-of-Experts 관련 초기화 전략은 대부분 공개되지 않음.
- DeepSeekMoE 및 DeepSeekV2는 표준 편차 0.006을 사용하는 정규 초기화를 채택.
- 밀집 모델에서는 Shoeybi et al. [157]에 의해 표준 편차 0.02를 사용하는 정규 초기화가 보편적.
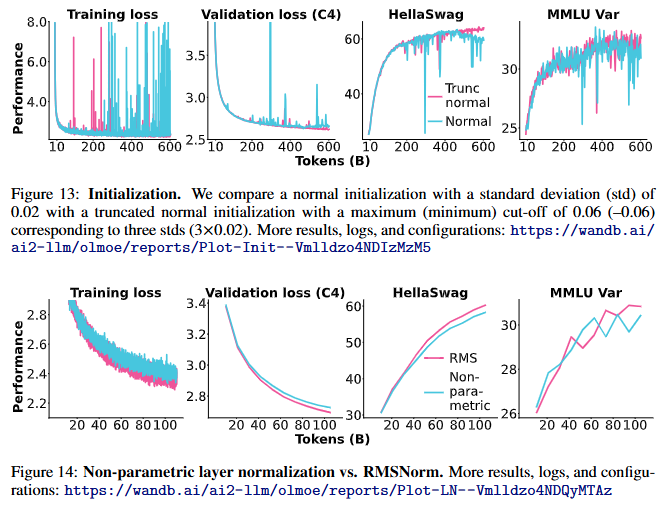
실험 결과 (Figure 13):
- 절단 정규 초기화 (Truncated Normal Initialization):
  - 정규 초기화보다 학습 안정성이 높고 성능이 우수.
  - 450B 토큰 학습 이후, 정규 초기화는 학습이 불안정해지는 반면, 절단 정규 초기화는 안정적으로 유지.
- 초기화 방식 외에는 동일한 설정으로 실험.
결론:
- OLMOE-1B-7B는 절단 정규 초기화를 사용하여 학습.

4.2.3 RMSNorm

배경

OLMo [64]는 비매개 변수(layer-parametric)를 사용하지 않는 Layer Normalization을 채택.
- 이는 일반적으로 사용되는 RMSNorm보다 속도가 훨씬 빠르기 때문.
RMSNorm 사용 모델:
- Llama, Gemma, Qwen 모델 계열 등이 RMSNorm을 사용.

실험 결과

Figure 14에 따르면, OLMo의 비매개 Layer Normalization을 RMSNorm으로 대체하면 성능이 향상.
- 이유:
  - 비매개 Layer Normalization은 기울기 스파이크(gradients spikes)를 많이 유발(Figure 16 참조).
  - 기울기를 1.0 으로 클리핑하여 이러한 스파이크를 제어했으나, 클리핑된 기울기는 실제 기울기가 아니므로 성능에 부정적 영향을 미칠 수 있음.
효율성 및 성능:
- RMSNorm을 사용하면 학습 처리량이 15% 감소.
- 하지만 성능 향상을 고려해 최종 모델에 RMSNorm 적용.
Weight Decay와의 조합:
- RMSNorm 파라미터를 Weight Decay에 포함시키는 것이 성능에 약간 더 유리(Figure 15 참조).
- 일반적으로 RMSNorm 파라미터는 Weight Decay에서 제외되지만, OLMOE-1B-7B에서는 포함.

4.2.4 Decaying Embedding Parameters

Embedding 파라미터와 Weight Decay

일반적 관행: Embedding 파라미터는 Weight Decay에서 제외.
실험 결과 (Figure 17):
- Embedding 파라미터를 Weight Decay에 포함하거나 제외하는 것은 성능에 미미한 영향을 미침.
- Weight Decay를 포함시키는 것이 약간 더 나은 성능을 보임.
결론:
- RMSNorm 파라미터와 함께 Embedding 파라미터도 Weight Decay에 포함.

4.2.5 QK-Norm

QK-Norm의 배경

QK-Norm:
- Query와 Key 프로젝션 후 Layer Normalization을 추가.
- 목적:
  - Attention 연산에서 발생할 수 있는 큰 logits 방지.
  - 네트워크의 안정성 개선.
  - 특히 저정밀 학습(low-precision training)에서 유용.

실험 결과 (Figure 18)

QK-Norm 사용 vs 미사용:
- QK-Norm을 적용하면 안정성과 성능이 향상됨.
- OLMo의 비매개 Layer Normalization을 사용하는 설정에서 안정성과 성능 개선 확인.
- RMSNorm을 사용하는 설정에서도 QK-Norm 적용 시 더 나은 학습 손실 및 기울기 크기 스파이크(grad norm spike) 방지.
효율성:
- QK-Norm 사용 시 처리량이 약 10% 감소.
결론:
- 최종 모델 OLMOE-1B-7B에 QK-Norm 사용.

4.2.6 AdamW Epsilon

AdamW 옵티마이저의 Epsilon 값

OLMo [64]:
- AdamW 옵티마이저에서 $\epsilon = 1E-05$ 를 사용.
- 큰 epsilon 값: 옵티마이저의 스텝 크기를 줄이는 대신, 안정성을 높임.

실험 결과 (Figure 19)

$\epsilon = 1E-08$ :
- AdamW의 권장 기본값( $\epsilon = 1E-08$ , [82])으로 설정 시 성능이 크게 향상.
- 안정성도 유지.
결론:
- 최종 학습에서는 AdamW 옵티마이저의 $\epsilon = 1E-08$ 로 설정.

4.3 Adaptation Settings (적응 학습 설정)

(1) 보조 손실 (Auxiliary Losses)

Load Balancing Loss (LLB):
- Zoph et al. [220]: 일반적인 미세 조정에서 LLB 사용 시 소폭의 성능 향상 보고.
- Shen et al. [154]: Instruction Tuning(SFT)에서는 LLB 및 Router Z-loss 사용의 성능 차이가 크지 않음을 보고.

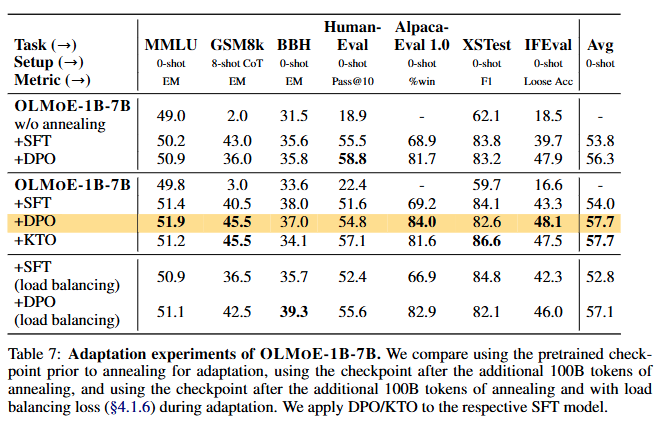
본 연구의 결과:
- Table 7에 따르면, LLB를 비활성화할 경우 더 나은 성능을 기록:
  - SFT 후: 54.0 (비활성화) vs. 52.8 (활성화).
  - DPO 후: 57.7 (비활성화) vs. 57.1 (활성화).
- 비활성화된 상태에서도 전문가 분포는 사전 학습과 크게 달라지지 않음 (Appendix G, Figure 33 참조).
결론:
- 적응 학습 중 Load Balancing Loss 비활성화.

(2) Checkpoint 사용 시점 (Annealing Checkpoint)

결과:
- *사전 학습 후 체크포인트(Post-Annealing)**를 사용하는 것이 더 나은 성능을 기록:
  - SFT 후: 54.0 (Post-Annealing) vs. 53.8 (Pre-Annealing).
  - DPO 후: 57.7 (Post-Annealing) vs. 56.3 (Pre-Annealing).
결론:
- Post-Annealing Checkpoint를 최종 적응 학습 설정으로 채택.

(3) 선호도 최적화 알고리즘 (Preference Algorithm)

DPO(Direct Preference Optimization):
- 선호도 최적화를 위한 다양한 알고리즘 중 하나.
KTO:
- KTO [54]와 DPO를 비교한 결과, 두 알고리즘이 유사한 성능을 보임.
- 하지만 AlpacaEval에서 DPO가 더 높은 점수를 기록, 데이터 오염 가능성이 낮음.
결론:
- 최종 OLMOE-1B-7B-INSTRUCT 모델에서 DPO 채택.

5. MoE Analysis (MoE 분석)

OLMoE-1B-7B는 개방형 및 비용 효율적인 모델로서 MoE 관련 연구를 확장합니다. 본 연구는 네 가지 MoE 특성에 대해 분석합니다:

5.1 Router Saturation (라우터 포화)

정의:
- 특정 중간 체크포인트 t와 최종 체크포인트 T에서 동일한 데이터 토큰에 대해 활성화된 전문가 ID의 비율.

$\text{Router Saturation}(t) = \frac{1}{N} \sum_{i=1}^{N} \frac{\lvert E_i(t) \cap E_i(T) \rvert}{k}$

N: 데이터셋의 총 토큰 수.
k: 각 입력 토큰당 활성화되는 상위 전문가 수.
결과:
- 초기 포화: 사전 학습 1%(5000 스텝, 20B 토큰)에서 이미 상위 8명의 전문가에 대한 라우팅이 약 60% 포화.
- 후기 포화: 사전 학습 40% 시점에서 포화율 80% 도달.
특징:
- 초기 레이어(예: Layer 0)는 다른 레이어보다 포화 속도가 느림.
- 이는 초기 레이어에서 부하 균형의 느린 수렴과 관련.
결론:
- 라우터는 사전 학습 초기에 대부분의 데이터를 특정 전문가로 안정적으로 라우팅.

5.2 Expert Co-activation (전문가 동시 활성화)

정의:
- 두 전문가 $E_i$ 와 $E_j$ 가 동시에 활성화된 비율.
- $\text{Expert Co-activation}(E_i, E_j) = \frac{N_{E_i, E_j}}{N_{E_i}}$
$N_{E_i, E_j}$ : 두 전문가가 동시에 활성화된 횟수.
$N_{E_i}$ : 전문가 EiE_i가 활성화된 총 횟수.
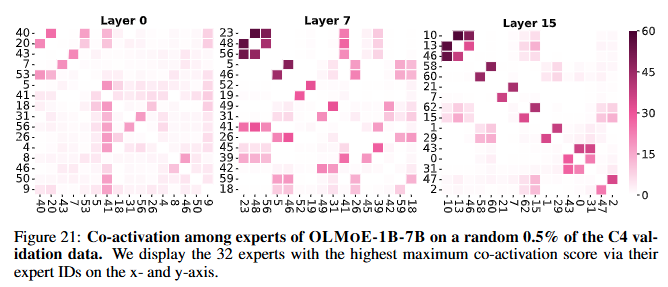
결과 (Figure 21):
- 특정 레이어 내에서는 전문가 간 강한 동시 활성화 없음.
- 레이어 7과 15에서 일부 전문가 그룹(2~3명)이 함께 활성화되는 경향 발견.
결론:
- 전문가 간 중복이 적음. 동시 활성화가 높은 전문가들은 통신 비용을 줄이기 위해 같은 장치에 배치 가능.

5.3 Domain Specialization (도메인 특화)

정의

특정 도메인 DD의 토큰 중 특정 전문가 EiE_i에 라우팅되는 비율을 도메인 특화라고 정의합니다:

$\text{Domain Specialization}(E_i, D) = \frac{N^{(k)}_{E_i, D}}{N_D}$

$E_i$ : 모델의 ii번째 전문가.
D: 데이터가 속한 도메인.
k: 고려되는 전문가 수 (예: k = 8일 경우, 라우팅 확률이 가장 높은 상위 8명의 전문가).
$N^{(k)}_{E_i, D}$ : DD 도메인의 토큰 중 EiE_i가 상위 kk 전문가에 포함된 횟수.
$N_D$ : MoE가 처리한 DD 도메인의 총 토큰 수.
의미:
- 값이 100%일 경우: 해당 도메인의 모든 데이터가 $E_i$ 로 라우팅됨.
- 값이 0%일 경우: 해당 전문가가 도메인 데이터 처리에 전혀 사용되지 않음.

실험 결과 (Figure 22)

특정 도메인에서 전문가의 활성화 비율이 랜덤 분포보다 높거나 낮음:
- arXiv: Layer 0의 첫 번째 전문가는 약 100%의 특화도를 보여 과학 텍스트에 매우 적합.
- C4(웹 크롤링 데이터): 전문가 활성화가 더 균형 잡혀 있으며, Load Balancing Loss가 효과적으로 작동함을 보여줌.
Mixtral-8x7B와 비교:
- Mixtral 모델은 도메인 특화도가 낮고, 모든 전문가가 균등한 라우팅을 보임.
- Mixtral은 밀집 모델에서 업사이클링된 모델로, 초기화가 전문가들의 특화 가능성을 제한했을 가능성이 있음.
결론:
- OLMOE-1B-7B는 전문가 간 중복이 적고 도메인별로 특화된 전문가를 활용.

5.4 Vocabulary Specialization (어휘 특화)

정의

특정 토큰 ID xx가 특정 전문가 EiE_i로 라우팅되는 비율을 어휘 특화라고 정의합니다:

$\text{Vocabulary Specialization}(E_i, x) = \frac{N^{(k)}_{x, E_i}}{N_x}$

$E_i$ : 모델의 i번째 전문가.
x: 분석 중인 토큰 ID.
$N^{(k)}_{x, E_i}$ : x가 $E_i$ 로 라우팅된 횟수.
$N_x$ : x가 모든 전문가로 라우팅된 총 횟수.
의미:
- 값이 100%일 경우: x 가 항상 $E_i$ 로 라우팅됨.
- 값이 0%일 경우: $E_i$ 가 해당 토큰 ID 처리에 전혀 기여하지 않음.

업로드중..

실험 결과 (Figure 23)

층별 특화:
- 나중 레이어에서 어휘 특화도가 더 높음.
- 나중 레이어는 입력 토큰보다는 예측된 출력 토큰 ID에 더 특화.
특정 전문가의 특화:
- Expert 27: 비알파벳 문자(키릴 문자, 데바나가리 문자 등)에 특화 ( $\sim 90\%$ ).
- Expert 43: 지리적 용어에 특화.
- Expert 48, 23: Then, Therefore와 같은 연결어에 특화. 이 두 전문가는 약 60%의 동시 활성화율(Figure 21)로 함께 작동.
도메인과의 연관성:
- GitHub 및 arXiv의 데이터를 처리하는 Layer 7의 Expert 4:
  - sq, YR(year), GHz와 같은 측정 단위에 특화.
  - 이는 과학 논문(arXiv) 및 GitHub 코드에서 흔히 사용되는 용어와 관련.

6. 관련 연구

MoE의 발전

대부분의 최신 언어 모델(LLM)은 여전히 Transformer 아키텍처를 기반으로 하지만, 다음과 같은 주요 변경 사항이 점진적으로 채택:
- SwiGLU 활성화 함수.
- RoPE(각도 기반 위치 인코딩).
- RMSNorm.
MoE 개선점:
- 라우팅 기법 [87, 144, 221 등].
- 세분화된 전문가 분할 [39, 68].
- 안정성 [220].
- 효율성 [86, 139, 48 등].
OLMOE의 기여:
- 5T 토큰 학습으로 과도한 학습(overtraining)을 수행.
- 기존 MoE와 밀집 모델 간 성능 한계를 분석.

7. 결론

OLMoE-1B-7B 및 OLMOE-1B-7B-INSTRUCT:
- 모델, 데이터, 코드, 로그를 포함한 완전한 오픈소스화.
- 활성 파라미터 1B, 총 파라미터 7B로 동급 모델 대비 최첨단 성능 기록.
- Llama2-13B-Chat 및 DeepSeekMoE-16B와 같은 더 큰 모델도 일부 작업에서 능가.
- Router Saturation, Expert Co-activation, Domain/Vocabulary Specialization 등을 분석하여 MoE 연구를 지원.

하임

NLP 공부합니당

이전 포스트

MoEAtt: A Deep Mixture of Experts Model using Attention-based Routing Gate

다음 포스트