오늘 학습 키워드
-
remove
-
stack
-
queue
-
tree
1. remove
-
#include <algorithm> -
범위 내에서 지우고 싶은 키는 뒤로 옮기고 남아있는 요소는 앞쪽으로 이동
(unique처럼 뒤로 옮겨진 키의 값은 undefined) -
"새 끝" 위치의 iterator를 반환
-
unique와 비슷 -
그래서 보통
erase()와 함께 사용
#include <algorithm>
#include <string>
#include <iostream>
int main() {
std::string s = "1020304050";
auto new_end = std::remove(s.begin(), s.end(), '0'); // 0빼고 앞으로
s.erase(new_end, s.end()); // 실제로 '0' 문자 삭제
std::cout << s << std::endl; // 출력: 12345
}2. stack
| 함수 이름 | 동작 | 간단한 예시 | 시간 복잡도 |
|---|---|---|---|
| stack::top() | top 요소 접근 | 해당 없음 | O(1) |
| stack::empty() | 스택이 비어 있는지 확인 | 해당 없음 | O(1) |
| stack::size() | 스택 내 요소 개수 반환 | 해당 없음 | O(1) |
| stack::push() | top에 요소 삽입 | s.push(value); | O(1) |
| stack::pop() | top 요소 제거 | 해당 없음 | O(1) |
| stack::push_range() | top에 범위 내 요소 삽입 | s.push_range(first, last); (반복자 first와 last로 정의된 범위) | O(N) (N은 삽입되는 요소 수) |
#include <stack>
using namespace std;
int main() {
stack<int> s;
s.push(10);
s.push(20);
cout << "스택의 top: " << s.top() << endl; // 20
s.top() = 40; // top의 반환자는 참조자이므로 수정 가능
s.pop(); // 40 제거
}- 문제 풀 때, basket같은 자료구조(LIFO)일 때 사용
3. queue
| 함수 이름 | 동작 | 간단한 예시(인자가 있으면 설명) | 시간 복잡도 |
|---|---|---|---|
| queue::front() | front 참조자 반환 | 참조자므로 front요소 없으면 에러 | O(1) |
| queue::empty() | 비어 있는지 확인 | 해당 없음 | O(1) |
| queue::size() | 요소 개수 반환 | 해당 없음 | O(1) |
| queue::push() | rear에 요소 삽입 | q.push(value); | O(1) |
| queue::pop() | front 요소 제거 | 해당 없음 | O(1) |
| queue::push_range() | 범위 내 요소 삽입 | q.push_range(first, last); (반복자 first와 last로 정의된 범위) | O(N) |
#include <queue>
using namespace std;
int main() {
queue<int> q;
q.push(1); // 큐: [1]
q.push(2); // 큐: [1, 2]
q.push(3); // 큐: [1, 2, 3]
cout << q.front() << endl; // 1
cout << q.back() << endl; // 3
cout << q.size() << endl; // 3
q.pop(); // 1 제거 → 큐: [2, 3]
q.front() = 99; // [99, 2]
if (!q.empty()) {
cout << "Queue is not empty." << endl;
}- 문제 풀 때, 원형 / 처음과 끝이 연결된 구조에서 큐 사용 가능
삽입, 삭제 걸리는 시간이 짧으므로, front로 접근 후 다음 요소 접근하는 방식을 front값을 rear로 push하고 front제거하는 방식으로 해결. 다음 요소가 이제 front가 됨
4. tree
-
tree구조는 STL이 없음
-
다만, set / map 등이 레드블랙트리(이진탐색트리)의 형태를 차용하여 사용
-
따라서, tree를 사용하려면 직접 구현해야함
구현법
1. 배열
-
out degree의 최댓값이 고정되어 있는 경우에만 사용 가능
-
이전
heap처럼 루트 node를 1번 인덱스로 하여 존재하는 node에 해당하는 배열에 값을 채움
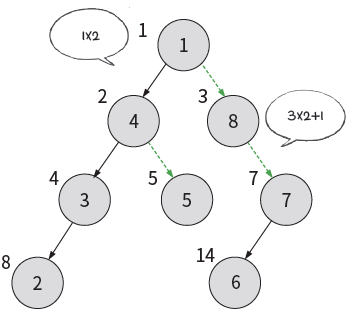

-
장점: 구현이 쉽고, 직관적이며 값 수정 쉬움
-
단점: 확장 제약이 큼, 실제 자손 node들에 비해 out degree의 최대값이 너무 크면 메모리 낭비가 크다
Binary Tree가 아니면 쓸 일 없음
2. 인접 리스트
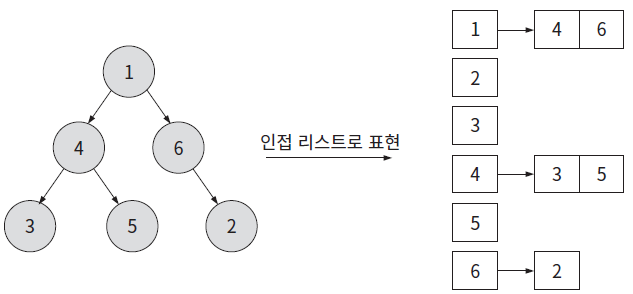
-
node를 담은 dataset과, 각 node의 자손들을 가지는 형태로 구현
-
unordered_map을 이용해 key값은 각 node를, value로는 각 자식 node를 가리키는 vector로 구현 가능
-
장점: 확장에 용이함, binary tree 아니여도 상관 없음
-
단점: 자식 node를 찾아갈 때 무조건 순회과정이 필요(비효율적)
순회
-
전위순회(NLR), 중위순회(LNR), 후위순회(LRN)으로 3가지 존재
-
전위순회는 tree구조를 복사할 때 유용
-
중위순회는 이진탐색트리에서 정렬된 값을 얻을 때 유용
-
후위순회는 tree구조를 삭제할 때 유용
이진탐색트리
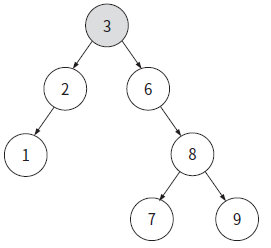
-
이진 트리에서 왼쪽 자식들은 부모보다 작고, 오른쪽 자식은 부모보다 큰 트리 형태
-
아래같은 상황(O(N))을 막기 위해 균형잡히게 트리를 수정하는데 그 예시가 set, map이 사용하는 레드블랙트리(O(logN))
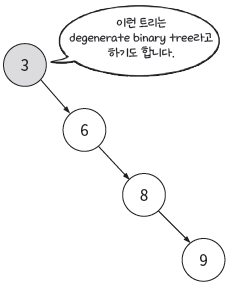
다음 학습
-
완전 이진 트리 구현
-
C++ 코딩테스트
