- Importance of Words in Documents
-
Search Engine에서 특정 검색어를 기준으로 14억 7천만 개의 문서의 순위를 어떻게 매길까?
-
가장 유명한 measure(측정 방법) : TF.IDF
-> TF : 단어가 자주 등장할수록 그 단어는 문서에 중요
-> IDF : 특정 문서에만 등장하는 단어일수록 그 단어는 문서에 중요
* Term Frequency (TF), 단어 빈도
: 특정 문서 내에서 단어가 얼마나 자주 등장하는지를 나타냄
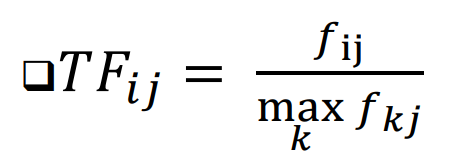
- fij : 단어 i가 문서 j에서 등장하는 빈도
- maxfkj : 문서 j에서 가장 많이 등장한 단어의 빈도
-> 단순 빈도 대신 정규화된 빈도를 사용하여 문서 길이에 따른 차이를 보정함!
* Inverse Document Frequency (IDF), 역문서 빈도
: 특정 단어가 전체 문서 집합에서 얼마나 희귀한지를 평가
-> 특정 단어가 여러 문서에서 자주 등장할수록 그 단어의 가중치를 낮추고, 반대로 적은 문서에서 등장할수록 가중치를 높임
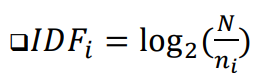
- ni : 단어 i가 등장하는 문서의 수
- N : 전체 문서의 수
* TF.IDF
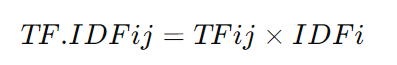
-> 문서 j에서 단어 i의 TF-IDF
-> 단어가 특정 문서 내에서 자주 등장하면서도 다른 문서에서는 잘 등장하지 않는 단어일수록 높은 가중치를 부여
- BM25 (Best Match 25)
: 정보 검색(Information Retrieval)에서 문서와 쿼리 간의 관련성을 평가하는 알고리즘
: 각 단어의 TF와 IDF를 곱한 값들을 문서 내 단어 수만큼 더한 값 ( 점수가 높을수록 문서가 쿼리와 더 관련이 있음)
-> 검색 엔진에서 문서 순위를 매길 때 자주 사용됨
-> TF-IDF의 발전된 버전
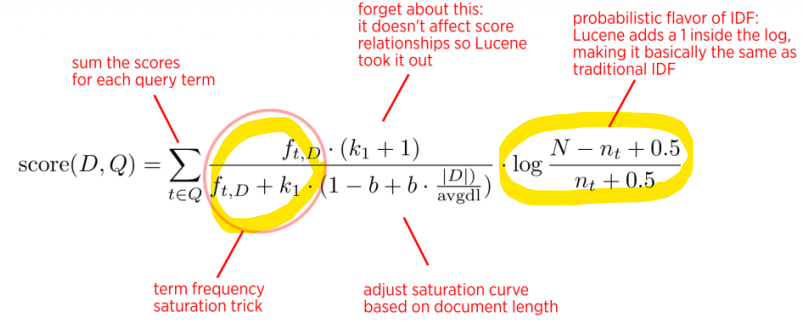
- 수식 속 TF
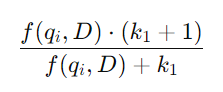
- 수식 속 IDF
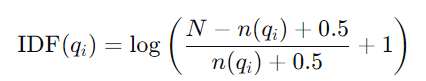
- 문서 길이에 대한 보정
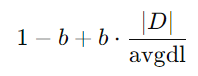

-> 문서의 길이가 평균보다 길면 가중치 감소, 평균보다 짧으면 가중치 증가시키는 역할
<TF-IDF와 BM25의 차이점>
- TF-IDF는 단순하게 단어 빈도를 정규화하여 사용하지만, BM25는 문서 길이와 단어 빈도의 포화 효과를 반영하여 더 세밀한 가중치를 계산
- BM25는 조정 매개변수 k1과 b를 통해 단어 빈도와 문서 길이에 대한 민감도를 사용자 정의 가능
- BM25가 더 정확한 관련성 평가
- Hash Functions
: key를 입력으로 받아 0부터 B-1(B : 전체 버킷 수) 범위의 버킷 번호를 출력하는 함수
ex) h(x) = x mod 19
-> 특정 항목을 빠르게 찾기 위해 사용됨 (= indexing)
<자료 구조에서의 좋은 해시 함수>
: 0부터 table 크기까지의 숫자를 반환해야 함
: 효율적으로 계산 가능해야 함, O(1) 시간
: 공간을 낭비하지 않아야 함
: 모든 index에 적어도 하나의 key가 hash되어야 함
: Load Factor(부하율) Lambda = (key 수 / 테이블 크기)
: Collision(충돌)을 최소화해야 함 -> 서로 다른 key가 동일한 index로 해시되는 경우를 줄여야 함
<Collisions과 그 해결 방법>
: Collision은 두 개의 다른 key가 동일한 값으로 hash될 때 발생
ex) Tablesize = 17일 때, key 18과 35가 동일한 값으로 해시됨
18 mod 17 = 1, 35 mod 17 = 1
-> 배열의 동일한 슬롯에 두 개의 데이터를 저장할 수 X
* Seperate Chaining (분리 연결법)
: 같은 슬롯으로 해시된 여러 항목을 저장하기 위해 Dictionary data structure(ex. linked list)를 사용
* Closed Hashing (폐쇄 해싱) or probing(탐사법)
: 두 번째 함수를 사용해 빈 슬롯을 검색하고, 찾은 첫 번째 빈 슬롯에 항목을 저장
<데이터 마이닝에서 좋은 해시 함수>
: 모든 B개의 버킷에 hash-key들이 대략 균등하게 분포하도록 하는 함수
ex) 모듈러 해시 함수 h(x) = x mod k (mod는 나눗셈의 나머지를 구하는 연산)
-> k로 Prime number(소수)를 선택하는 것이 가장 좋음
- Index
: 객체의 한 가지 또는 여러 요소의 값을 통해 객체를 효율적으로 검색할 수 있게 해주는 데이터 구조
- index를 구축하는 여러 방법
: 해시 테이블, B-tree...
- Secondary Storage
Disk
: 블록으로 구성됨 ( = 운영 체제가 주 메모리와 디스크 간 데이터를 이동할 때 사용하는 최소 단위)
: 일반적인 블록 크기: 약 64 kBytes
: 블록 접근 및 읽기 시간 : 약 10 밀리초
: 주 메모리에서 단어를 읽는 것보다 10^5배 느림
: 최대 속도 : 약 100 Megabytes/초
- 10 Terabytes의 데이터를 디스크에서 읽는 데 약 1일 소요
-> 대량의 데이터를 효율적으로 처리하기 위해서는 index나 cache같은 기술을 사용해 디스크 접근을 최소화해야 함
- Base of Natural Logarithms
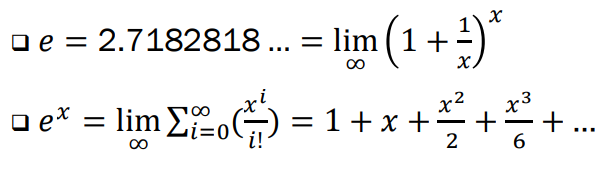
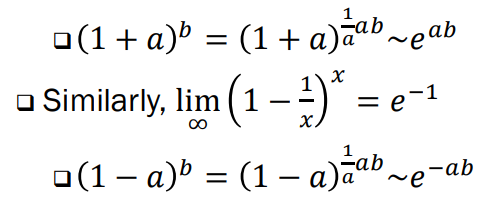
-> 이러한 근사치는 a 가 작을 때 잘 작동함
- Power Laws (거듭제곱 법칙)
: 한 변수가 일정 비율로 증가하면 다른 변수는 그에 대한 거듭제곱으로 증가하는 관계
: 한 변수의 변화가 다른 변수의 거듭제곱(즉, 제곱, 세제곱 등)으로 표현되는 관계
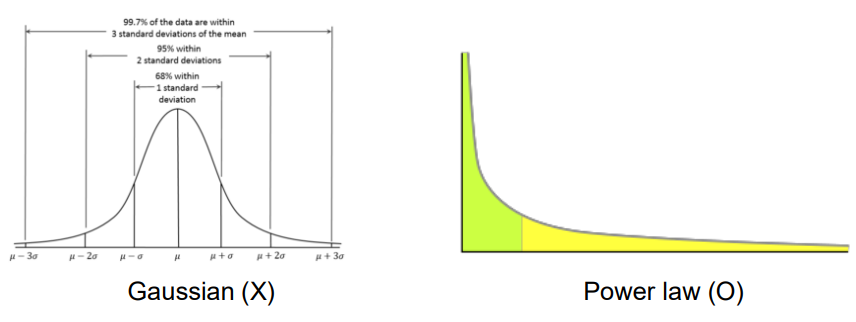
- 일반적으로, x와 y가 거듭제곱 법칙 관계에 있을 때, log y가 log x에 대해 선형
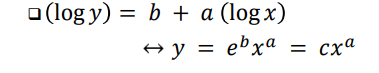
: 거듭제곱 법칙은 현실세계의 데이터 특성을 더 잘 이해하는 데 도움을 줌
- Matthew Effect : 부자는 더 부자가 된다.
<거듭 제곱 법칙의 예시>
: 웹 그래프에서의 노드 연결 수
: 제품 판매량
: 웹사이트 크기
: 도시 인구