- Cost function

- Backpropagation algorithm
- Gradient computation: Forward propagation
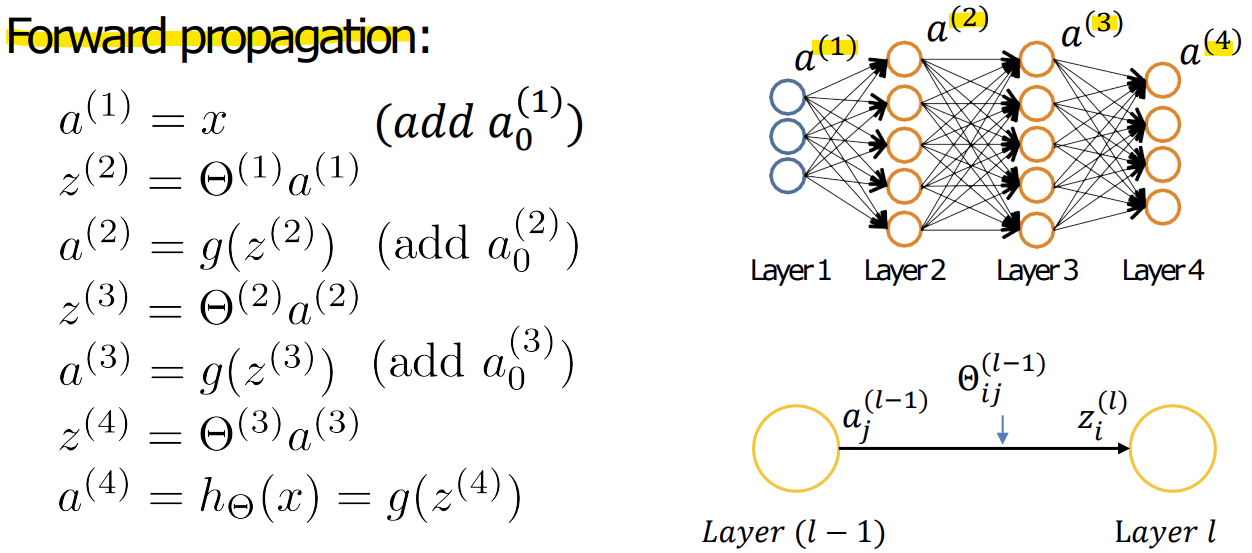
- Gradient computation: Backpropagation algorithm


-> forward propagation에서 계산된 예측값과 실제값의 차이를 기반으로 오차를 계산
-> 해당 오차를 역방향으로 전달하면서 각 가중치가 손실에 얼마나 영향을 미쳤는지 계산(출력층 및 은닉층의 error 계산)
-> 계산한 error들을 이용해 각 가중치에 대한 손실함수의 Gradient를 계산

-> 계산한 Gradient를 이용해서 가중치를 업데이트
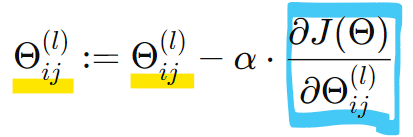
<Forward propagation과 Backpropagation의 전체 흐름>
1) 순전파(Forward Propagation): 입력 데이터를 통해 출력값을 계산
2) 손실 함수 계산: 예측값과 실제값의 차이로 손실을 구함
3) 역전파(Backpropagation): 오차를 역방향으로 전달하며 각 레이어의 오차를 계산
4) Gradient 계산: 오차와 활성화 값을 이용해 가중치에 대한 그래디언트를 구함
5) 경사 하강법으로 가중치 업데이트: 계산된 그래디언트를 이용해 가중치를 조정
6) 이 과정을 반복하며 신경망이 점점 더 정확한 예측을 할 수 있도록 학습
-> 예측 오차를 기반으로 가중치를 조정해 성능을 개선함
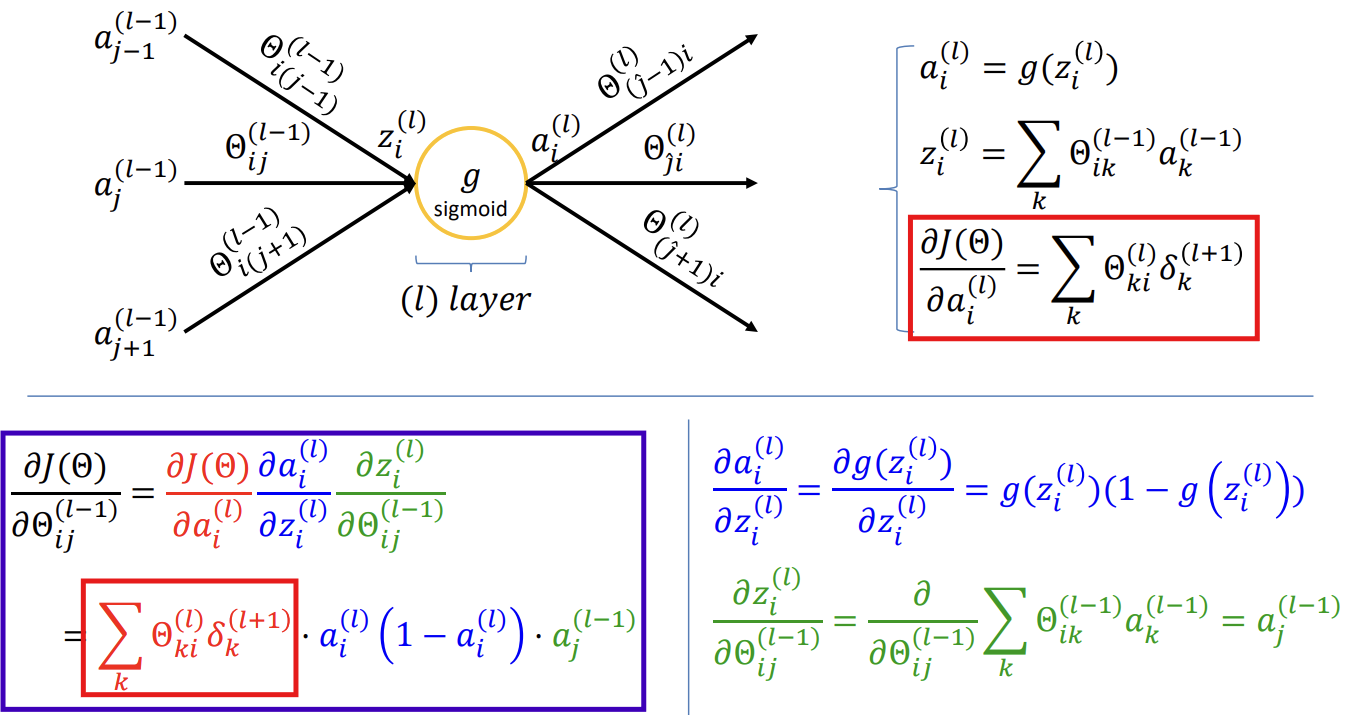
- Node를 통해서 어떻게 값이 역전파되는가?
-> 각 층의 출력값은 그 이전의 가중합과 활성화 함수를 거쳐 만들어지기 때문에, 가중치와 손실 간의 관계를 직접 계산하기 어렵기 때문에, 오차를 작은 단계로 나눠서 추적함
-> 체인 룰을 통해 가중치와 손실 간의 관계를 추적하기 위해:
J를 직접 가중치에 대해 미분할 수 없으므로 중간 단계인 z를 거쳐야 함
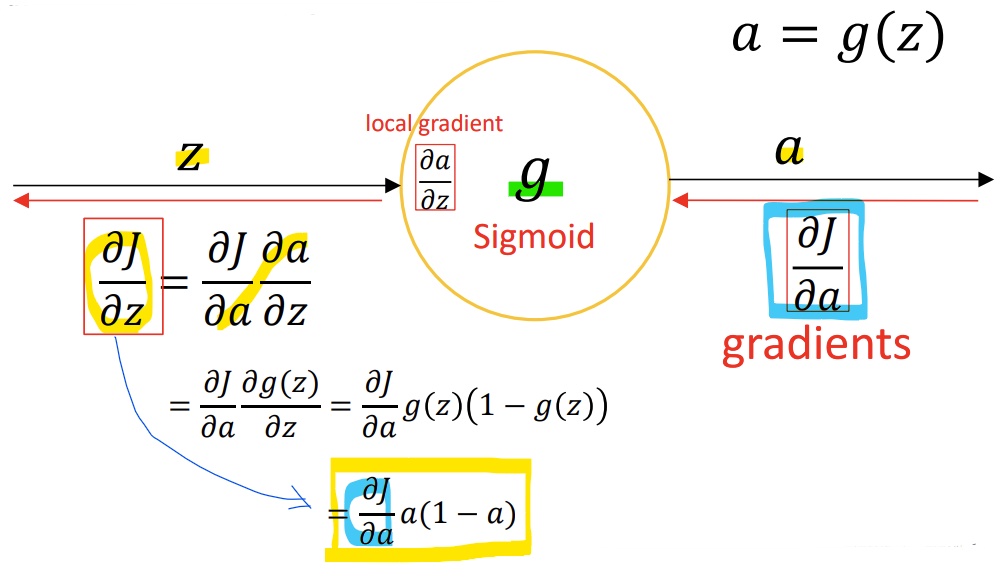
-> Chain rule을 사용하기 때문에 값이 역전파됨
- Weight값 update와 역전파 값
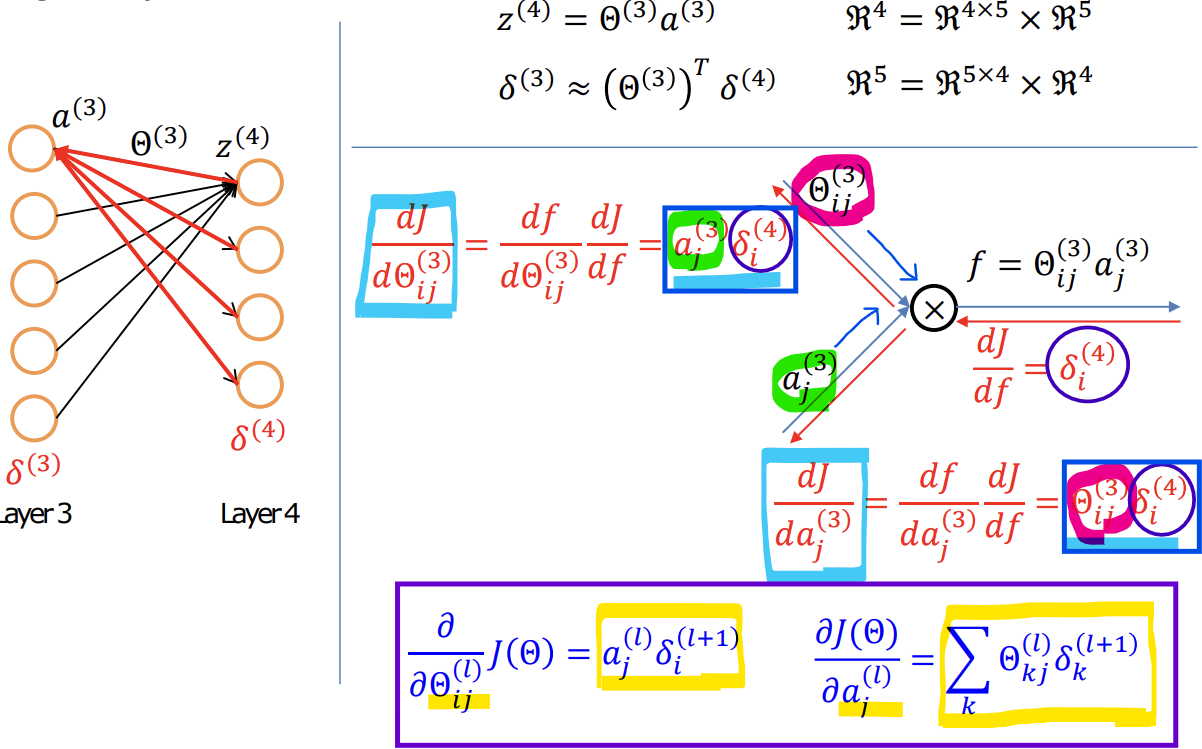
-> 손실 함수를 가중치에 대해서 미분한 식: 해당 레이어(l)의 입력값 이전 레이어(l + 1)에서 계산한 에러값
-> 손실 함수를 입력값에 대해서 미분한 식: 해당 레이어(l)의 가중치값 이전 레이어(l + 1)에서 계산한 에러값
- Implementation Detail for backpropagation

-> (4)는 5x1, (5)는 4x1이므로 차원이 맞지 않음!
-> 입력값 a(3)에 1을 하나 추가해서 (5)를 5x1로 만듦
-> 계산 가능!
- Backpropagation algorithm


- Backpropagation intuition
- Forward propagation
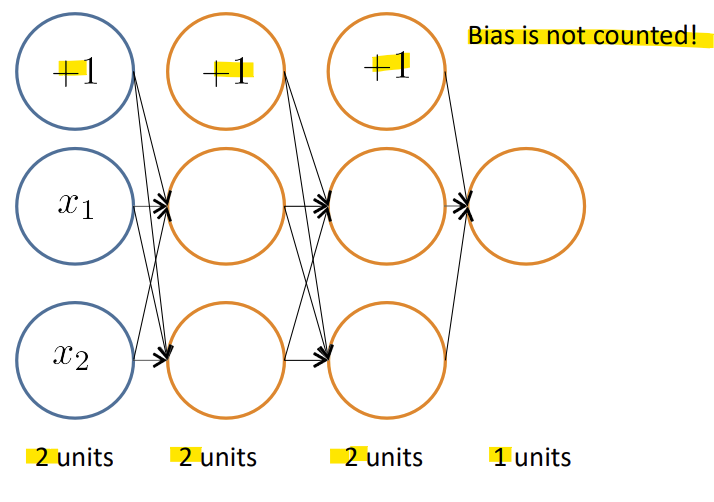
-> Bias는 해당 layer의 unit 수에 포함하지 않음!
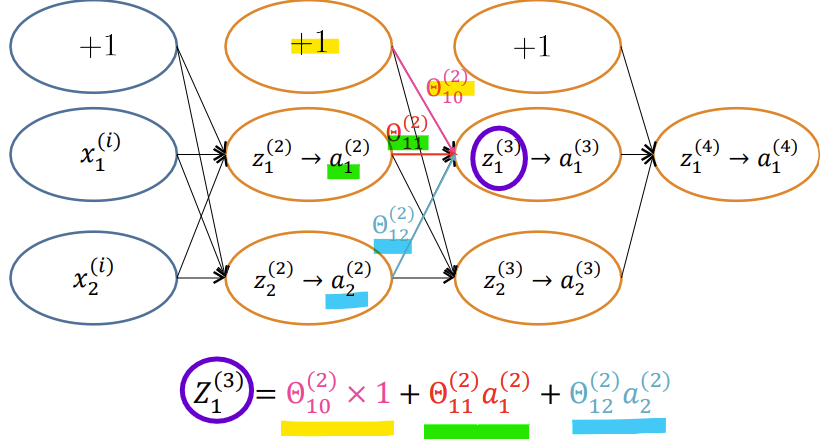

1) 손실 함수 J(Θ)는 예측값과 실제값 간의 차이를 측정하는 함수
2) 역전파는 손실 함수의 값을 최소화하기 위해 가중치에 대한 기울기(Gradient)를 계산함
3) 체인 룰을 사용해 각 레이어의 오차를 전파하며, 가중치를 업데이트하는 데 필요한 정보를 수집함
4) 최종 목표는 가중치를 조정해 신경망의 예측 성능을 개선하는 것
- Back Propagation (Intuition)
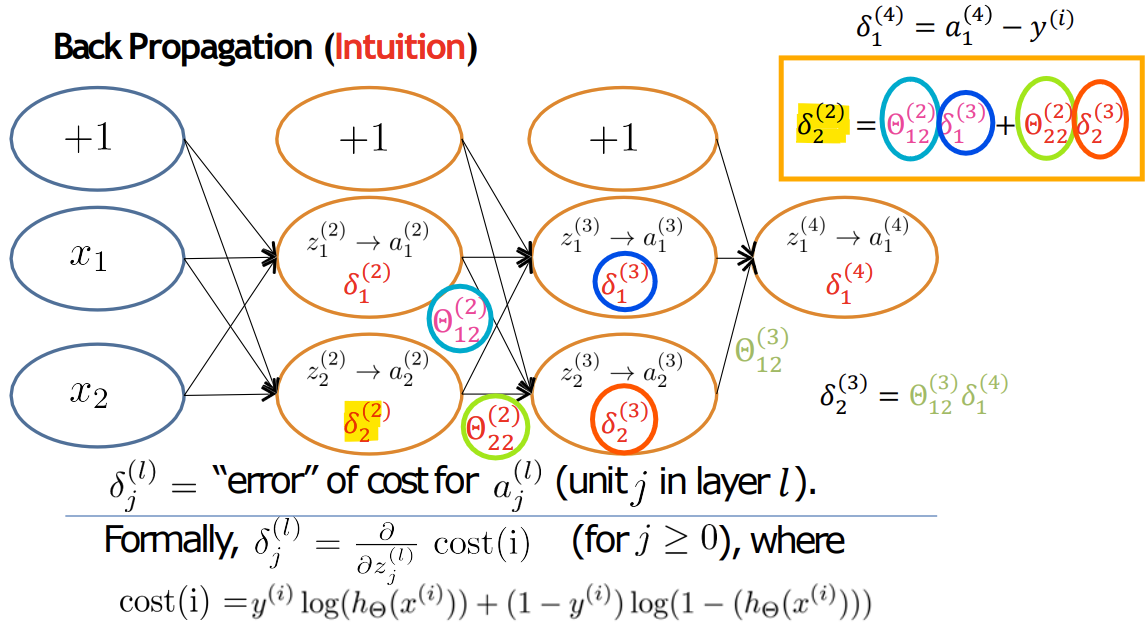
- 출력층 오차 계산식
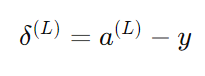
- 은닉층 오차 계산식

-> 반드시 활성화 함수의 미분이 포함되어야 함
- theta 초기화 값 주의
- theta가 0이면 업데이트가 안됨! -> 수렴 X
- theta가 1이면 모두가 똑같이 업데이트됨
- 대칭 깨짐(Symmetry Breaking) 문제
: 가중치를 모두 동일한 값으로 초기화하면, 신경망의 각 뉴런이 동일한 입력을 처리하게 되고, 결과적으로 동일한 출력을 내게 됨
: 이로 인해 뉴런들이 각각 고유한 특징을 학습할 수 없게 되는 문제가 발생함- 가중치가 너무 크면
: 뉴런의 출력값이 큰 값을 가지게 되어, 특히 시그모이드(Sigmoid)나 타난(Tanh) 같은 비선형 활성화 함수에서는 출력이 포화 영역에 들어가게 됨
: 포화 영역에서는 미분값이 거의 0에 가까워지기 때문에, 역전파(Backpropagation) 시 기울기(Gradient)가 사라지는 현상(Gradient Vanishing)이 발생할 수 있음- 가중치가 너무 작으면
: 뉴런의 출력이 매우 작은 값을 가져, 활성화 함수의 출력 역시 0에 가까워짐
: 이로 인해 기울기가 거의 전달되지 않거나, 학습 속도가 매우 느려짐
-> 절대 동일한 값으로 초기화하면 안됨!
-> random 초기화해야 함!
- Gradient checking

-> 코드가 잘 작성된 것인지 확인하는 Debugging 과정



-
Implementation Note:
Backpropagation을 구현하여 DVec(unrolled 벡터 형태)을 계산
Numerical Gradient Check(수치적 기울기 확인)을 구현하여 gradApprox(근사 기울기)를 계산
두 값이 유사한지 확인
기울기 확인을 끄고, Backpropagation 코드를 사용하여 학습을 진행 -
Important:
분류기를 학습시키기 전에 기울기 확인 코드를 반드시 비활성화
경사 하강법(Gradient Descent)의 매 반복(iteration) 또는 costFunction(…)의 내부 루프에서 수치적 기울기 계산을 실행하면 코드가 매우 느려질 수 있음
- Random initialization
- Gradient descent와 advanced optimization method에서는 theta의 초기값이 필요함

- Zero initialization
1) 모든 theta를 0으로 초기화 시
: identical되기 때문에 안됨!
2) theta가 너무 크면
: exploding 문제 발생
3) theta가 너무 작으면
: gradient vanishing문제 발생
4) theta가 symmetry(대칭적)이면
: identical됨<unit이 identical하다의 의미>
- 각 뉴런(Units)이 동일하게 동작한다는 의미
- 여러 개의 뉴런이 같은 가중치와 같은 활성화 함수를 가지고 있으며, 동일한 입력을 처리할 때 동일한 출력을 생성하게 됨
- 모든 뉴런이 동일한 출력을 생성하게 됨(모든 뉴런이 같은 역할을 함)
-> 역전파 과정에서 오차가 각 뉴런에 동일하게 적용되어 가중치가 동일하게 업데이트됨
-> 뉴런들이 독립적으로 다른 특징을 학습할 수 X
- 결론: theta는 랜덤 초기화 해야함! -> Symmetry breaking
- Random initialization: Symmetry breaking
- Symmetry breaking(대칭 깨짐)
: 뉴런들이 서로 다른 특징을 학습할 수 있도록 하는 방법
: 모든 뉴런이 동일하게 동작하지 않도록 가중치를 무작위로 초기화하는 과정

<Training a newral network 전체 과정>
1) 가중치 무작위 초기화
2) 순전파(Forward propagation) 구현
3) 비용 함수 J(theta) 계산 코드를 구현
4) 역전파(Back propagation) 구현
5) Gradient Checking 사용
: 역전파로 계산한 J(theta)의 기울기와 수치적으로 계산한 J(theta)의 기울기의 근사값을 비교(Debugging)한 후, Gradient checking 코드 비활성화하기
6) 경사 하강법 or 고급 최적화 방법을 사용하여 역전파와 함께 theta를 매개변수로 하는 비용 함수 J(theta)를 최소화하려고 시도
