DP - 15989번: 1, 2, 3 더하기 4

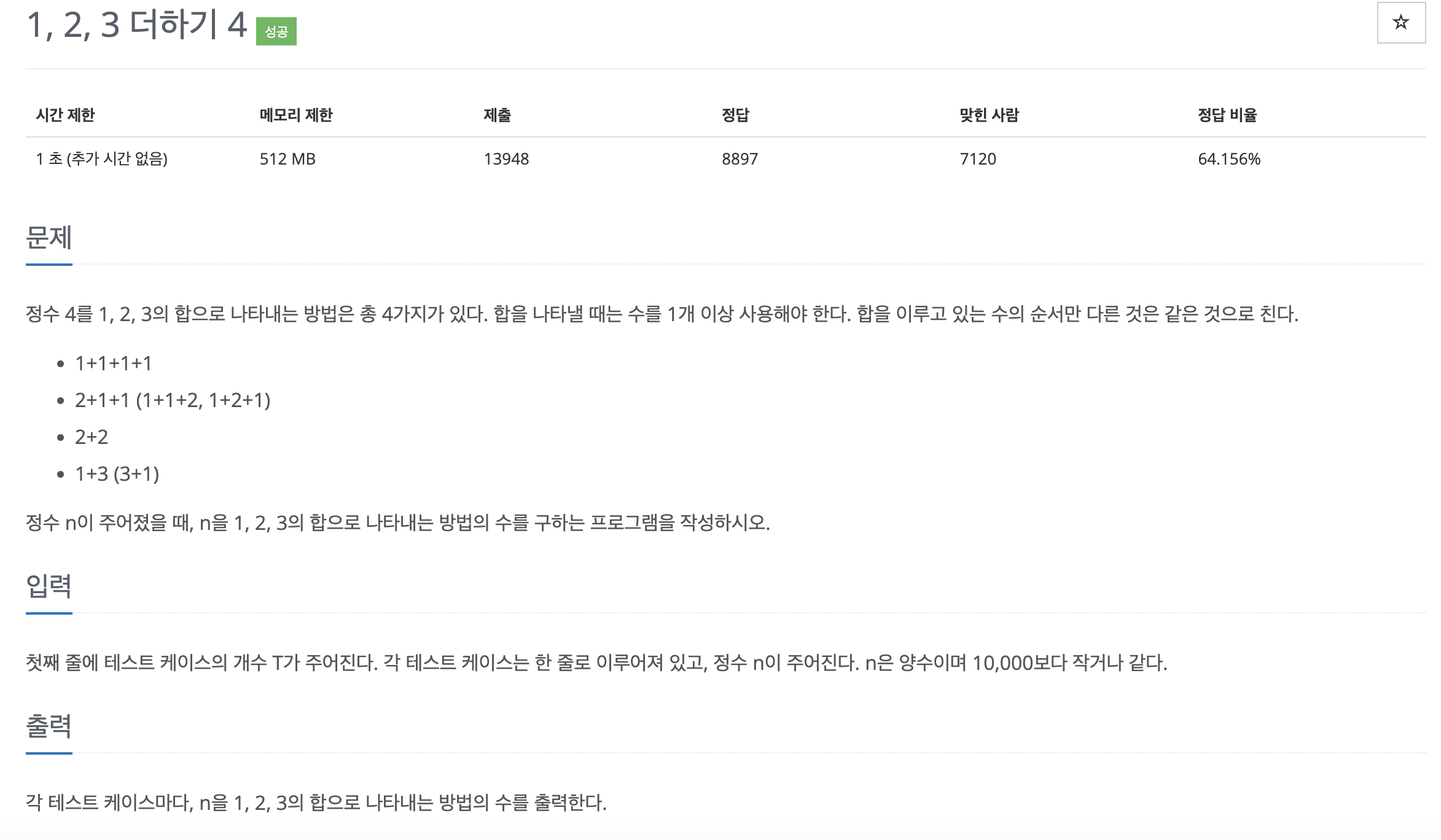
DFS로 풀면 작은 n에서는 잘 되지만, n이 커지면 경우의 수가 너무 많아 시간초과가 발생
-> DP로 풀어야 함!

t = int(input())


'''
def dfs(target, now, num_list, total_set, last):

    if now == target:
        #num_list.sort()  # 정렬한 후 존재 유무 확인으로 중복 피하기!

        total_set.add(tuple(num_list))
        # set에 리스트는 넣지 못하므로 tuple로 변환하여 추가
        return


    for add in [1, 2, 3]:
        if add < last: # 직전에 넣은 수보다 작으면 스킵!
            continue
        if now + add <= target:
            dfs(target, now + add, num_list + [add], total_set, add)
    '''
    # 3이 들어갈 수 있다면
    if now + 3 <= target:
        # num_list_3.append(3)
        dfs(target, now + 3, num_list + [3], total_set)
    # 2가 들어갈 수 있다면
    if now + 2 <= target:
        # num_list_2.append(2)
        dfs(target, now + 2, num_list + [2], total_set)
    # 1이 들어갈 수 있다면
    if now + 1 <= target:
        # num_list_1.append(1)
        dfs(target, now + 1, num_list + [1], total_set)
    '''
    return
'''

def count_combinations(n):
    dp = [0] * (n+1)
    dp[0] = 1

    for num in [1, 2, 3]:
        for i in range(num , n + 1):
            dp[i] += dp[i - num]
    
    return dp[n]

for _ in range(t):
    n = int(input())

    #total_set = set()

    #dfs(n, 0, [], total_set, 1)

    # print(total_set)
    # print(len(total_set))

    print(count_combinations(n))