DP - 등굣길(Lv.3)

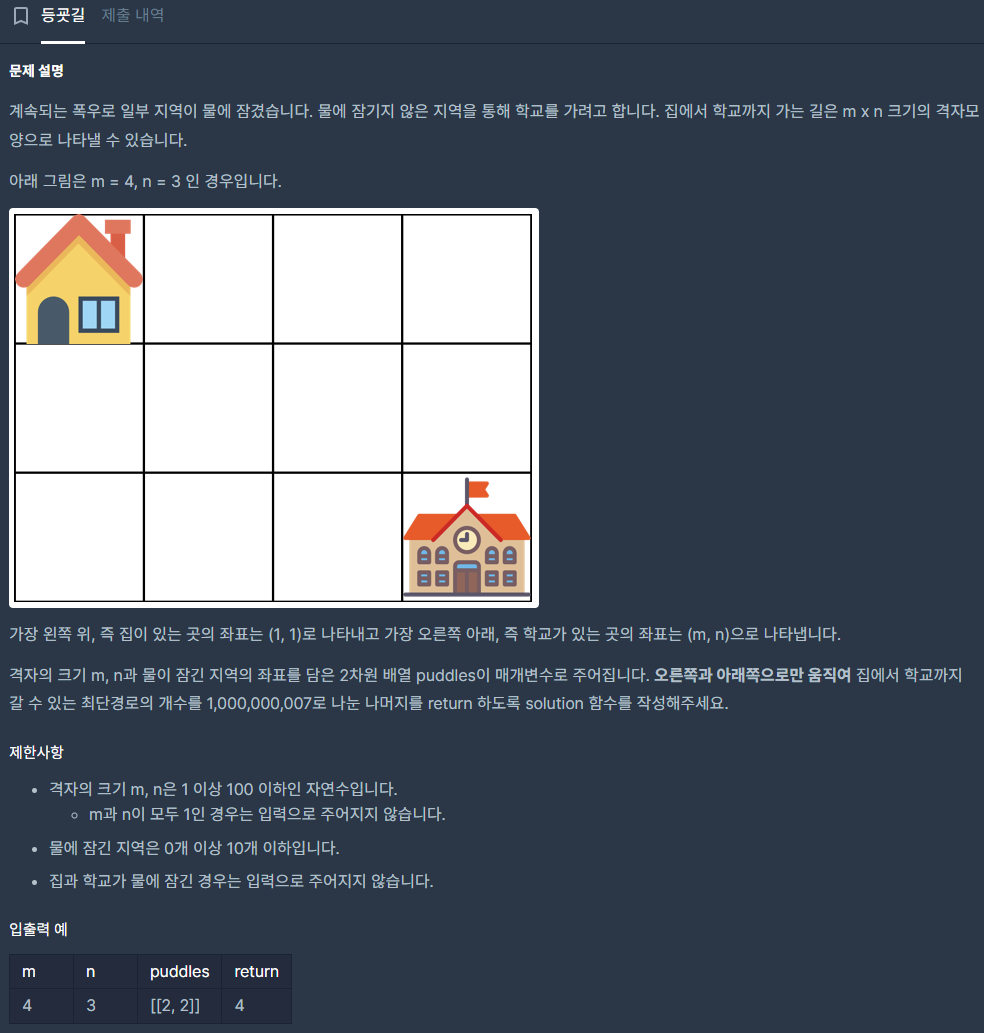
• 오른쪽(→)과 아래(↓) 이동만 허용하므로 총 이동 횟수는 항상 (n−1)+(m−1)로 고정됨!
• dp[i][j]에 (0,0)에서 (i,j)까지 올 수 있는 최단 경로 개수를 저장
• 물웅덩이 칸은 dp=-10으로 표시해 계산에서 제외
• dp[i][j] = dp[i - 1][j] + dp[i][j - 1] (왼쪽과 위에서 내려오는 경우를 더해주면 됨)

- 항상 좌표 순서 주의하기 -> dp[y][x]

from collections import deque

MOD = 10 ** 9 + 7


def solution(m, n, puddles):
    answer = 0
    
    # 좌표를 0 기준으로 재설정
    dp = [[-1] * m for _ in range(n)]
    for puddle in puddles:
        # 좌표 순서 주의! dp[y][x] 순으로 해야 함!
        dp[puddle[1] - 1][puddle[0] - 1] = -10
        
    dp[0][0] = 1
    
    for i in range(n):
        for j in range(m):
            # 물웅덩이인 경우
            if dp[i][j] == -10:
                continue
            # 시작점인 경우
            if i == 0 and j == 0:
                continue
            
            sum = 0
            # 위에서 내려오는 경우
            if i - 1 >= 0 and dp[i - 1][j] != -10:
                sum += dp[i - 1][j]
            # 왼쪽에서 오는 경우
            if j - 1 >= 0 and dp[i][j - 1] != -10:
                sum += dp[i][j - 1]
            
            dp[i][j] = sum

    answer = dp[n - 1][m - 1]
        
    return answer % MOD