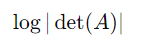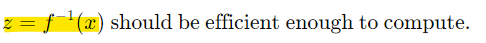- Normalizing Flow(정규화 흐름)
- 정규화 흐름은 가역적 변환(invertible transformation)을 사용하여 단순한 분포에서 데이터 분포를 추정
- 단순히 로그 우도(log-likelihood) 목표만으로 모델을 학습 가능
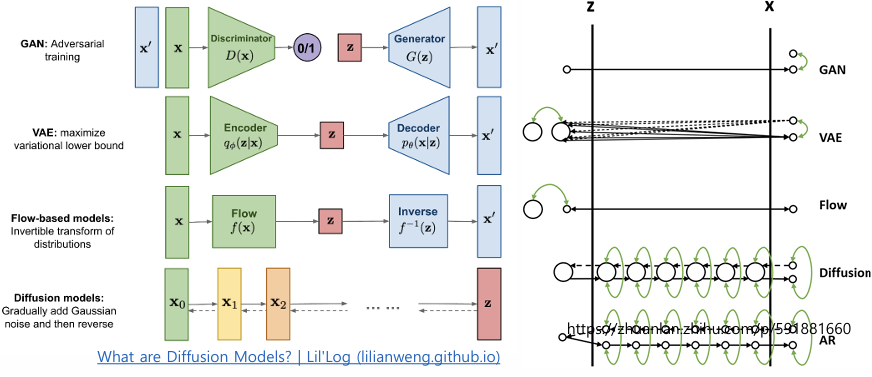
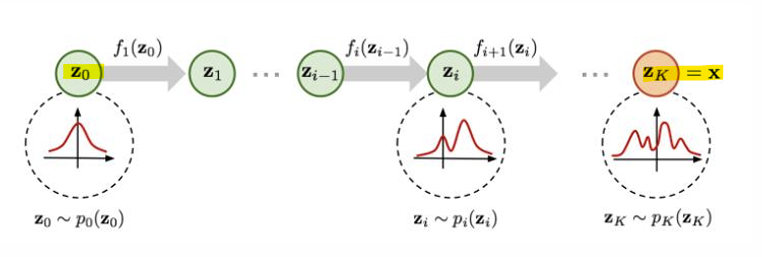
- Normalizing Flow
: 단순한 분포를 시작으로 가역적 변환을 통해 복잡한 데이터 분포를 학습하는 방법
-> 학습 과정에서 로그 우도 최대화를 사용하며, 우도 계산과 샘플링에 유리
-> 효율적인 변환 함수와 가역성 덕분에 밀도 추정, 샘플링, 추론 등 다양한 작업에 활용 가능
-
변수 변환 정리를 사용해 변수 z와 x 간의 변환 관계에서 확률밀도함수(PDF)를 계산하는 방법
-
주어진 조건:
변수 x는 변수 z에 대해 변환 함수 f를 적용하여 생성됨
x=f(z)
z의 확률 분포 pZ(z)는 알려져 있음(ex. 가우시안 분포) -
목표: x의 확률 밀도 함수 pX(x)를 계산하는 것
- 변수 변환 정리(Change of Variable Theorem)
- 확률 분포는 총 확률이 항상 1이어야 한다는 성질을 따름
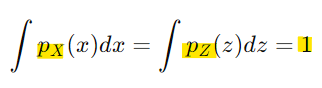
즉, 변수 변환 후에도 총 확률은 변하지 않아야 함
이를 기반으로 확률 밀도를 다음과 같이 계산 가능
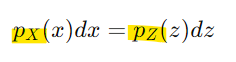
-> dz와 dx는 각 변수의 작은 변화량
- 변환된 확률 밀도 함수:
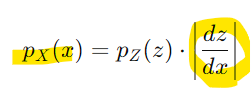
dz/dx는 z와 x의 관계를 나타내는 야코비안(Jacobian)

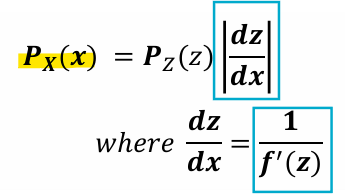
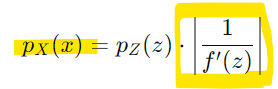
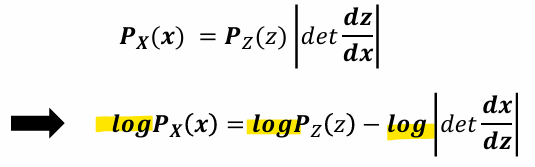
-> 확률 밀도를 직접 계산하는 대신 로그 확률 밀도를 사용하면 곱셈 연산을 덧셈으로 바꿀 수 있어 계산이 효율적
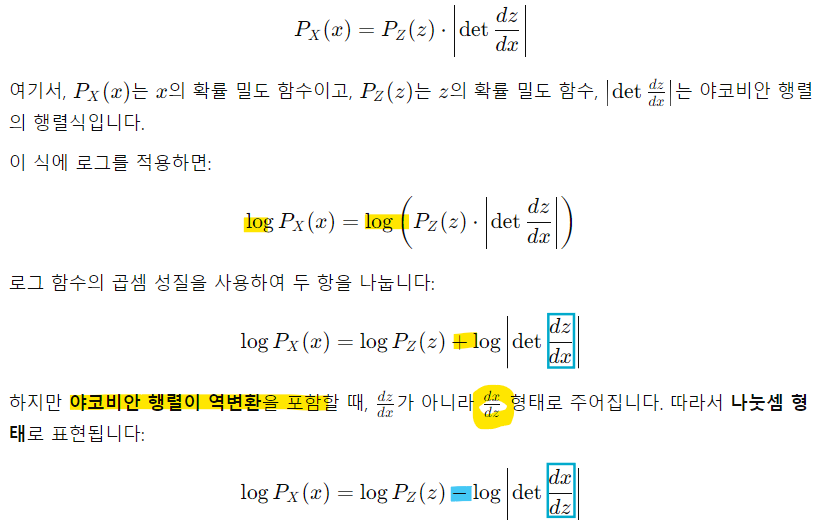
(분모와 분자를 바꾸면 로그에서 부호가 바뀜)
-> z를 f-1(x)로 변환

- 야코비안 행렬식의 역할:
야코비안 행렬식은 변수 변환 과정에서 데이터 공간이 얼마나 "확장" 또는 "축소"되었는지 나타냄
-> 예를 들어, 특정 공간에서 확률 밀도가 축소되면, 해당 구간의 확률 값은 증가함
역변환의 필요성:
x에서 z로의 변환(f-1)을 통해 P(x)를 P(z)로 계산할 수 있음(z의 확률밀도가 이미 알려져 있다는 가정)
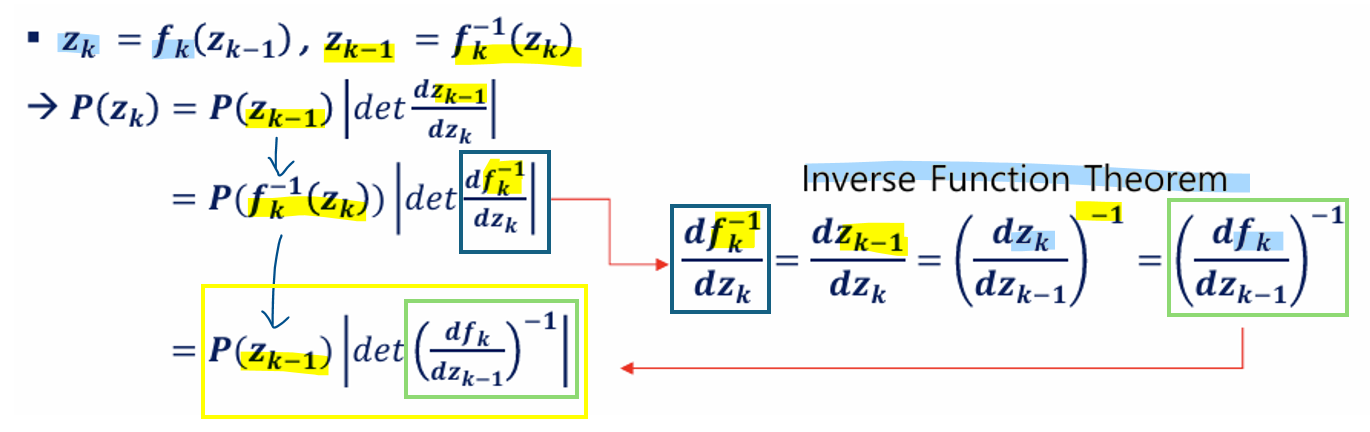
- 역함수 정리
: 함수 f:Rn →Rn이 가역적(invertible)이고, 역함수 f-1가 존재한다고 가정
: 역함수 정리는 f의 야코비안 행렬(Jacobian Matrix)이 특정 조건을 만족하면 f−1도 연속적이고 미분 가능하다는 사실을 보장함
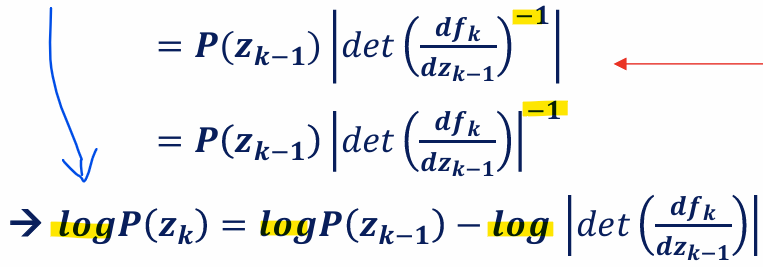
-> 곱셈 연산을 덧셈과 뺄셈으로 단순화하여 계산 효율성을 높이기 위해 로그를 사용
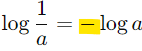





- Maximize log-likelihood
- 목표: 로그 우도를 최대화하여 데이터 분포 P(x)를 학습
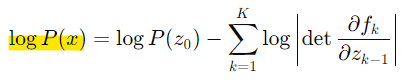

< 변환 조건 >
1) 변환 fk는 가역적(invertible)이어야함
- 이유
:가역성(invertibility)은 logP(x)를 계산하거나 샘플링을 수행할 때 필수적
z = f-1(x): x에서 z로의 역변환이 계산 가능해야 샘플링 및 확률 계산이 효율적
2) 야코비안 행렬식이 계산 가능해야 함
- 이유:
야코비안 행렬식은 각 변환 단계에서 확률 밀도를 계산하는 데 핵심적
행렬식 계산이 비효율적이면 모델 학습 속도가 크게 저하
3) 역변환 계산이 효율적이어야 함
- 이유:
샘플링 과정에서 역변환이 필수적이므로 계산 효율성이 중요
역변환이 복잡하거나 계산 비용이 높다면 실시간 샘플링이나 학습에 큰 제약이 발생
- Affine Coupling Layer
- Affine Coupling Layer는 Normalizing Flow에서 사용되는 효율적인 변환 기법
- 특정 채널의 절반을 고정(keep)한 후 나머지 절반에 대해 Affine Transformation (선형 변환 + 이동 변환)을 적용
-> 이 방식은 계산 효율성을 유지하면서도 가역성을 보장


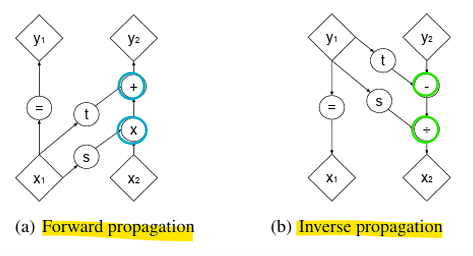
(a) Forward Propagation
- x1 (고정된 데이터)는 그대로 y1로 전달
- x2는 t와 s 함수에 의해 스케일 및 이동 변환 후 y2로 전달
(b) Inverse Propagation
- y1은 그대로 x1로 복원
- y2는 이동 변환 t를 제거하고, 스케일 변환 s의 반대(역수)를 적용하여 x2로 복원
- Affine Coupling Layer에서 야코비안(Jacobian) 행렬과 그 행렬식(determinant)을 계산하는 과정
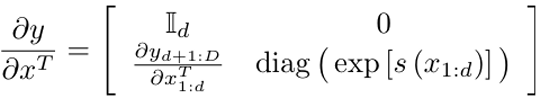

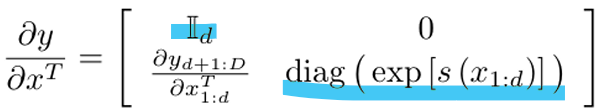

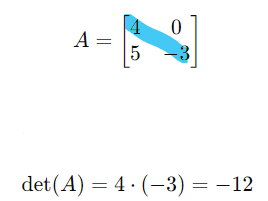
<주요 특징>
1) 효율적인 계산
야코비안 행렬식 계산이 단순히 대각선 요소의 곱으로 처리되므로, 복잡한 연산 없이 효율적으로 계산 가능
2) 로그 행렬식
로그 행렬식 계산이 단순히 스케일 s(x1:d)의 요소별 합산으로 변환되므로, 추가적인 비용이 들지 않음
3) Affine Coupling Layer의 설계
야코비안 행렬의 대각선 구조는 Affine Coupling Layer에서 설계상 자연스럽게 만들어지며, 이로 인해 계산 효율성이 극대화
- RealNVP
- Using a stack of coupling layers(Affine coupling layers)
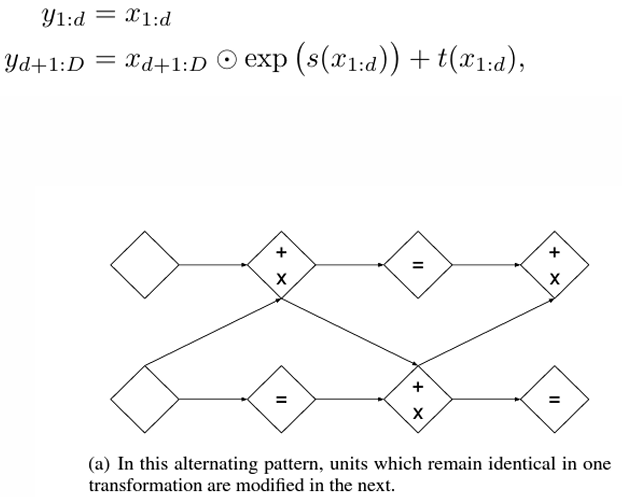
- Affine Coupling Layer의 동작과 스택 구조(Stack of Coupling Layers)
- 여러 개의 Coupling Layer를 사용하여 입력 데이터의 모든 부분이 번갈아 가며 변환되도록 설계된 구조
<여러 Coupling Layer가 필요한 이유>
- 단일 Coupling Layer에서는 입력 데이터의 절반만 변환되고, 나머지 절반은 변환되지 않고 그대로 유지됨
-> 이를 보완하기 위해 여러 개의 Coupling Layer를 스택(Stack)으로 쌓아 변환되지 않은 데이터도 번갈아가며 변환되도록 설계함(모든 부분이 변환)
- Partitioning (데이터 분할)
-> 데이터를 절반으로 나누어 일부는 고정하고, 나머지 부분만 변환함
-> 이를 구현하기 위해 데이터의 구조에 따라 적절한 마스킹 기법을 사용
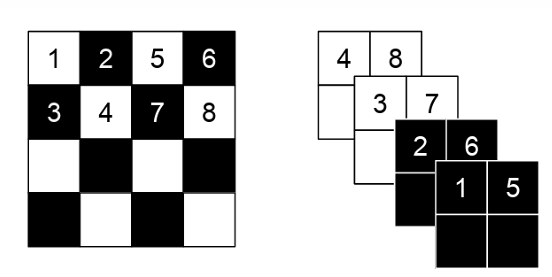
1) Spatial Checkerboard Pattern Mask
- 데이터 공간(Spatial)을 기반으로 체커보드 패턴을 사용하여 픽셀을 선택
- 흰색과 검은색 패턴처럼 데이터의 절반만 변환하고 나머지 절반은 고정
ex) 2D 이미지 데이터의 경우, 체커보드 패턴으로 픽셀을 선택:
흰색 픽셀은 변환되지 않고 고정
검은색 픽셀만 변환
2) Channel-wise Mask
- 데이터를 채널별로 나누어 일부 채널은 고정하고, 나머지 채널을 변환
- 채널 정보(예: RGB 이미지의 R, G, B 채널)를 기준으로 분리하여 변환을 수행
ex) 4채널 텐서를 두 부분으로 나눔:
첫 번째 절반의 채널은 고정
두 번째 절반의 채널은 변환
- Multi-scale architecture
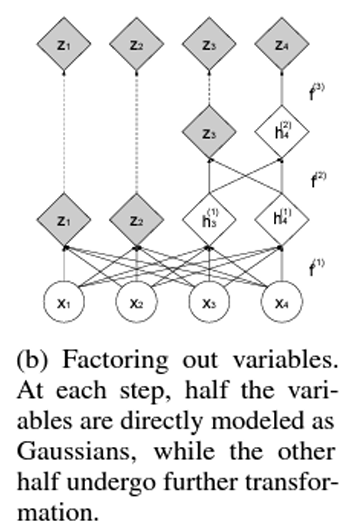
-
Factoring Out Variables
-
데이터를 다중 스케일로 나누고, 일부 변수는 변환 과정을 거치지 않고 직접 모델링
-
데이터의 절반을 변환에서 제외하며, 이 변수들은 최종적으로 가우시안 분포(Gaussian Distribution)로 직접 매핑됨
-
Gaussians로 직접 모델링
-
목표는 데이터를 점차적으로 가우시안 분포로 변환하는 것이므로, 중간 변수들이 이미 가우시안 분포라면 추가 변환이 필요 없음
-> 이를 통해 계산량을 줄이고, 효율적으로 모델링 가능
<동작 방식>
1) 변수 분리 (Factoring Out)
- 입력 데이터 x를 절반씩 나누어 처리:
첫 절반: 변환을 통해 더 복잡한 분포로 변환
나머지 절반: 바로 가우시안 분포로 매핑하여 모델링
2) 나머지 변수는 변환 진행 - 남은 절반의 변수들은 Affine Coupling Layers 등을 사용하여 점진적으로 변환 과정을 거침
이렇게 변환된 변수들은 다시 일부를 가우시안으로 매핑하며, 이 과정을 반복
<특징>
- 최종 목표가 데이터를 가우시안 분포로 변환하는 것이므로, 중간 변수들이 가우시안 분포를 따르는 것은 문제가 되지 않음
-> 따라서 중간 과정에서 직접 가우시안 분포로 매핑하는 것이 가능(학습 효율성 상승) - 변환을 반복하며 데이터를 다중 스케일로 처리
-> 이 과정은 전체 데이터의 복잡한 구조를 점진적으로 단순화하고, 학습 과정을 안정화시킴
-> 네트워크 깊이가 너무 깊을때, 특정 부분은 가우시안일 것이라고 가정 -> 일부 layer만 통과시킴 -> 효율적 학습
- Glow
- Glow는 RealNVP에서 사용된 고정된 데이터 채널 순서 뒤집기를 개선하여, 학습 가능한 1×1 컨볼루션(Learnable 1x1 Convolution)을 도입한 모델
-> 더 유연하고 표현력 있는 모델
- RealNVP - 고정된 순서 뒤집기
- Affine Coupling Layer 전에 채널의 순서를 뒤집는 고정된 패턴(permutation)을 사용
- 일반적으로 채널 순서를 역순으로 바꾸는 방식
-> Affine Coupling Layer는 입력 데이터를 절반씩 나누어 처리함
-> 따라서 데이터의 모든 채널이 번갈아가며 변환되도록 순서를 뒤섞어야 전체 데이터가 고르게 변환됨
- 제한점
: 고정된 순서 뒤집기 방식은 유연성 부족, 데이터에 최적화된 순서를 학습 불가
-> 이는 모델의 표현력을 제한
- Glow - Learnable 1x1 Convolution
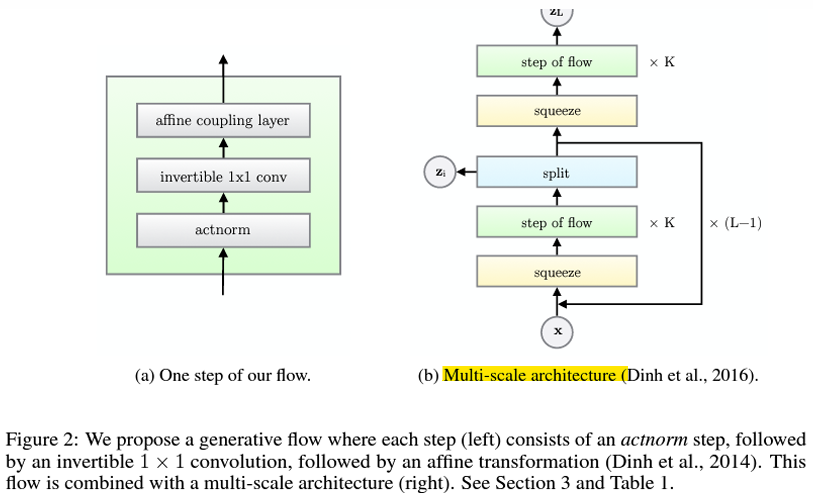
- Glow는 RealNVP의 고정된 순서 뒤집기를 대체하여, 학습 가능한 1×1 컨볼루션을 도입(Heuristic methods)
-> 채널 간 선형 변환을 수행

-> W는 역행렬 계산이 가능한 정사각 행렬로 설계됨
-> 학습 과정에서 W는 데이터에 최적화된 채널 간의 선형 조합을 학습
-> 역변환 시에는 W-1를 사용하여 효율적으로 역연산을 수행
<장점>
1) 유연한 채널 변환
고정된 순서 뒤집기와 달리, 1×1 컨볼루션은 데이터에 최적화된 변환을 학습
이는 모델의 표현력을 높이며, 복잡한 데이터 패턴을 더 잘 캡처함
2) 가역성 보장(Invertible)
W는 가역 행렬로 설계되므로, W-1을 사용하여 역변환이 가능함
-> 모델은 항상 확률 밀도 함수의 정방향 및 역방향 변환을 효율적으로 수행 가능
3) 계산 효율성
1×1 컨볼루션은 텐서의 각 채널에 독립적으로 적용되므로, 계산 비용이 낮고 효율적
- Log-determinant: 행렬의 행렬식(determinant)에 로그(log)를 취한 값