1. 유향선분이란?

유향선분(directed segment)은 방향을 갖는 선분(line segment)을 말한다.

시작점이 A이며 종점이 B인 유향선분 AB가 있다고 할 때, 유향선분의 속성은 아래와 같다.

• 점 A의 위치
• B에 관한 방향
• AB의 크기(길이)

---

2. 벡터란?

벡터(vector)는 방향과 크기를 추상화한 양이다. 유향선분 AB의 대표 벡터를 $\overrightarrow{AB}$ 혹은 $\vec{a}$ 혹은 굵은 문자 $\boldsymbol{a}$ 등으로 표현한다.

2-1. 벡터의 성분 표시

벡터는 다음과 같이 화살표선으로 그려지는데, 이를 좌표 평면에 배치하여 표현할 수 있다. 시작점을 원점에 놓고 종점의 좌표로 벡터를 나타내는 것을 벡터의 성분 표시라고 한다.

이때 벡터의 성분 표시는 종점의 좌표인 $(a_1, a_2)$

2-2. 벡터의 크기

벡터를 나타내는 화살표선의 길이를 벡터의 크기라고 한다. $\vec{a}$의 크기는 $|\vec{a}|=\sqrt{{a_1}^2+{a_2}^2}$ 이다.

---

3. 벡터의 내적

벡터를 곱할 때는 크기와 방향을 고려해야 한다. 벡터의 내적이란 크기(스칼라)만을 고려한 벡터의 곱셈을 말한다. $\vec{a}$, $\vec{b}$ 의 내적은 $\vec{a}\cdot\vec{b}$이다.

$\theta$는 $\vec{a}$, $\vec{b}$가 구성하는 각도다.

3-1. 코시-슈바르츠 부등식

$\cos\theta$는 $-1\le\cos\theta\le1$의 범위를 같는다. 여기에 벡터의 크기 $|\vec{a}||\vec{b}|$를 대입하면,

$|\vec{a}||\vec{b}|\cos\theta=\vec{a}\cdot\vec{b}$ (벡터의 내적) 이므로,

이 성립니다. 이를 코시-슈바르츠 부등식이라고 한다.

내적이란 두 벡터가 어느정도로 같은 방향을 향하고 있는가다. 코시-슈바르츠 부등식에서 알 수 있는 3가지가 있다.

1. 두 벡터가 반대 방향일 때 내적은 최솟값을 갖는다.
2. 두 벡터가 평행하지 않을 때 내적은 반대 방향일 때와 평행일 때의 중간값이다.
3. 두 벡터가 평행할 때 내적의 최댓값을 갖는다.

즉, 두 벡터가 같은 방향을 향할수록 내적은 커진다.

3-2. 내적의 성분 표시

앞서 벡터의 성분 표시를 $\vec{a}=(a_1,a_2)$ 로 나타냈다. 이를 내적의 성분 표시로 표현하면 아래와 같다.

3차원이라면,

$\vec{a}=(2,3,2), \vec{b}=(5,1,-1)$ 경우,

---

4. 벡터의 일반화

지금까지는 2,3차원의 벡터를 살펴보았다. 2,3차원의 벡터의 성질을 수만 차원의 벡터로 확장할 수 있다. 따라서 신경망의 경사하강법에서 벡터를 사용하게 된다.

이제 n차원의 벡터를 살펴보도록 한다.

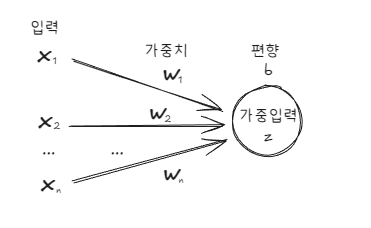
위와 같은 신경망이 있을 때 가중 입력 $z=w_1x_1+w_2x_2+...+w_nx_n+b$이다.

이 가중 입력 $z$를 벡터로 간주하여 다뤄보자.

입력 $x$와 가중치 $w$를 벡터의 성분으로 표시하면,

$z$를 내적 형태로 바꾸면,

4-1. 텐서(tensor)

텐서(tensor)란 물리학의 변형력 텐서를 수학적으로 추상화한 것이다. 벡터의 개념을 확장한 것으로 동일한 성질의 벡터를 행렬로 표기한다.

응력이란 외부에서 힘을 가하면 그 힘을 내부에서 버티려고 생기는 힘 혹은 면적을 말한다.

$\sigma$ : 응력 (stress)
$F$ : 힘이 작용하는 단면적 (area)
$A$ : 물체에 작용하는 외력 (force)

변형력 텐서란 응력을 수학적으로 표현한 2차 텐서다. 외부 힘이 가해지는 경우 물체 내부에서는 힘의 방향과 면의 방향(법선)에서 두 방향을 모두 가져야 하기에 2차 텐서가 필요하다.

참고로 변형력 텐서는 3x3의 행렬인데, 이는 3차원 공간에서의 3개의 면과 3개의 힘 방향을 모두 표현한다.