격자형 구조에 관한 포스트와 BFS 포스트를 참고하면 좋다.
얼음틀 문제
N x M 크기의 얼음 틀이 있다. 구멍이 뚫려 있는 부분은 0, 칸막이가 존재하는 부분은 1로 표시된다. 구멍이 뚫려 있는 부분끼리 상, 하, 좌. 우로 붙어 있는 경우 서로 연결되어 있는 것으로 간주한다. 이때 얼음 틀의 모양이 주어졌을 때 생성되는 총 아이스크림의 개수를 구하는 프로그램을 작성하시오. 다음의 4 X 5 얼음틀 예시에서는 아이스크림이 총 3개 생성된다.
00110
00011
11111
00000입력 조건
- 첫 번째 줄에 얼음 틀의 세로 길이 N과 가로 길이 M이 주어진다. (1≤N,M≤1,000)
- 두 번째 줄부터 N+1번째 줄까지 얼음 틀의 형태가 주어진다.
- 이때 구멍이 뚫려있는 부분은 0, 그렇지 않은 부분은 1이다.
출력 조건
- 한 번에 만들 수 있는 아이스크림의 개수를 출력한다.
문제 해석
문제에서는 0이 연결된 부분의 개수를 묻고 있다. 답을 얻기 위한 과정은 다음과 같다.
- 특정 위치에서 연결된 0을 모두 찾기(방문하기).
- 방문하지 않은 0을 찾아 1번 과정을 반복
- 2번 과정을 반복하여 연결된 0의 묶음의 개수를 구하기
알고리즘
문제를 해결하기 위해서는 주어진 2차원의 배열을 모두 탐색해야한다. 즉 모든 위치를 방문하여 해당 인덱스의 값이 조건에 맞는지 확인해야 한다.
이때 사용할 수 있는 알고리즘은 DFS, BFS이다. DFS와 BFS를 구현하는 코드는 해당 알고리즘을 사용하는 문제에서 반복되어 활용된다. 따라서 각 알고리즘의 구현하는 틀을 기억해 둘 필요가 있다.
2차원의 배열로 이루어진 격자형 구조에서 탐색을 할 때 주로 사용되는 dxdy기법과 큐를 사용하는 너비우선탐색 BFS을 사용하여 문제를 해결해보겠다.
문제 풀이
전체 구조
풀이의 큰 틀은 다음과 같다.
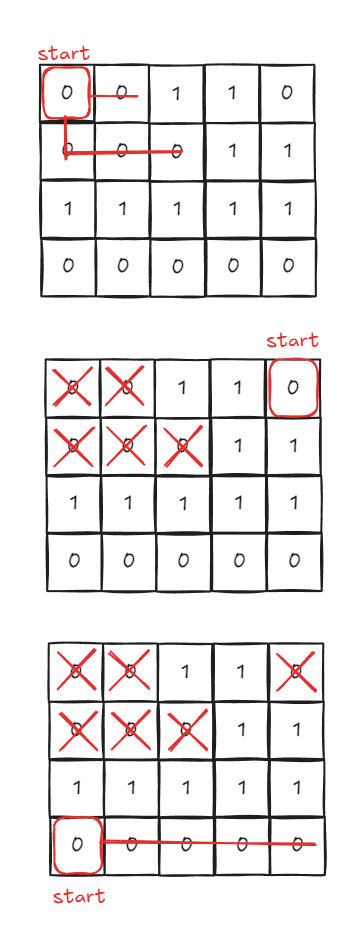
그림처럼 격자형의 그래프가 있을 때 graph[0][0] 부터 탐색을 시작하여, bfs로 연결된 0을 찾는다.
더이상 연결된 0이 없을 시 반복문으로 방문되지 않은 0 (그림 상에서는 X 표시가 없는)을 찾는다.
결과 값은 start된 횟수를 반환하면 된다.
탐색의 조건
dxdy로 bfs 탐색의 기준을 잡게 되는데, 그래프 인덱스를 벗어난 탐색을 막기 위해서는 그래프 범위를 기준으로 탐색 불가능한 경우를 걸러줘야 한다.
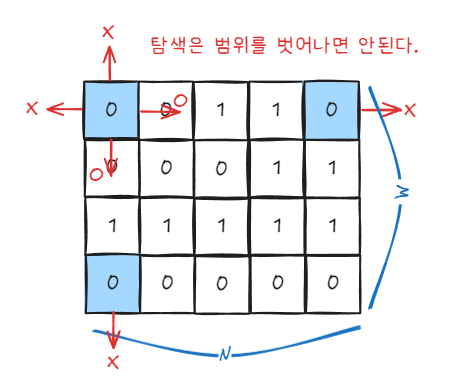
len(graph)=N 이며 len(graph[i])=M (, 정수) 라고 하자.
현재 위치에서 탐색을 할 때 방문 가능 조건을 크게 2가지로 잡을 수 있다.
- 인덱스 관점 : x축은 0에서 N사이, y축은 0에서 M사이
- 값(해당 위치에 담긴 값) : 0 중에서 방문하지 않은 0.
탐색 과정
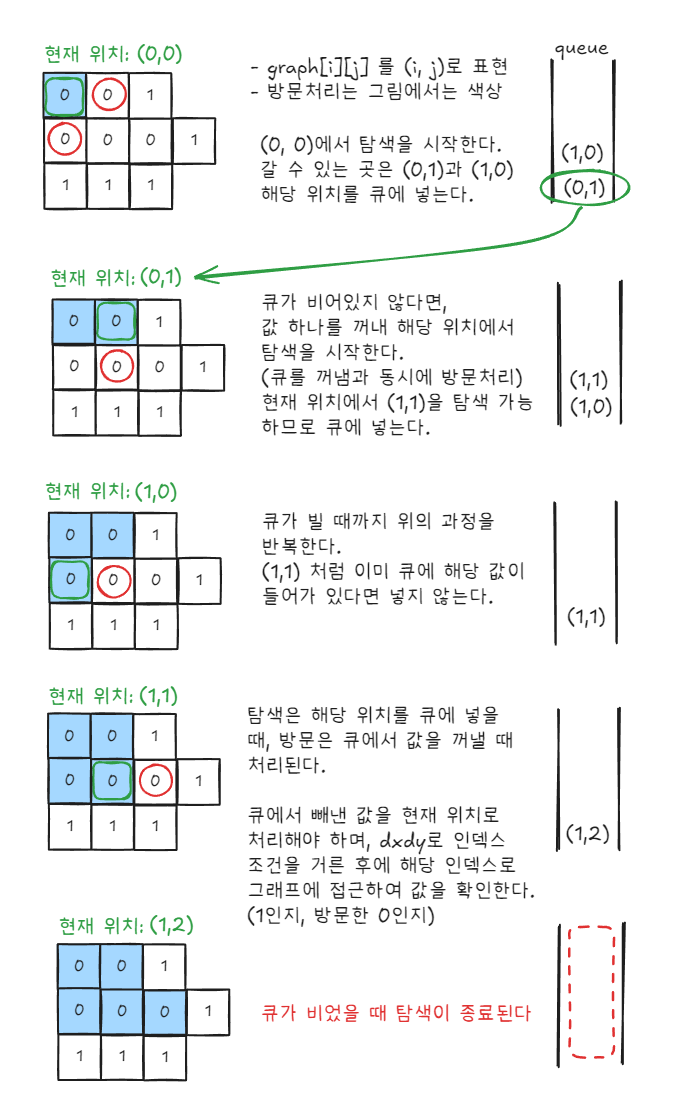
이렇게 하나의 탐색이 종료되면 answer 변수를 하나 만들어 값을 증가시킨다. 하나의 얼음틀을 찾았다는 의미다.
이후 반복문을 통해 그래프의 값으로 접근하여 1이 아니며 방문되지 않은 0을 찾는다. 이때 구분을 위해 방문 리스트를 따로 만들지 않고, 방문한 0의 그래프 값을 아예 바꾸는 방향으로 가겠다.
위의 구조를 파이썬 코드로 구현해보았다.
코드로 구현
풀이 1
from collections import deque
dx = [-1,0,1,0]
dy = [0,1,0,-1]
def bfs(sx,sy):
dq = deque([]) # 빈 큐 선언
dq.append([sx,sy]) # 시작 노드 추가
while dq:
[cx, cy] = dq.popleft() # 큐에서 꺼낸 노드를 현재 위치로
if graph[cx][cy] == 2: # 방문 했다면
continue
graph[cx][cy] = 2
for i in range(4): # 4방향 탐색
nxtX = cx + dx[i] # 다음 x 좌표
nxtY = cy + dy[i] # 다음 y 좌표
# 인덱스 범위를 벗어나는지 확인
if nxtX < 0 or nxtY < 0 or nxtX == N or nxtY == M:
continue
# 방문 여부를 확인
elif graph[nxtX][nxtY] != 0: # 1, 2
continue
dq.append([nxtX, nxtY]) # 다음 탐색 위치 추가
def solution(N,M,graph):
answer = 0
for i in range(N):
for j in range(M):
if graph[i][j] == 0: # 방문하지 않은 노드 찾기
bfs(i,j) # 해당 위치에서 bfs 시작
answer += 1 # 얼음틀 추가
return answer입력 부분은 아래와 같이 작성할 수 있다.
N, M = list(map(int, input().split()))
graph = [list(map(int, input().strip())) for _ in range(N)]
풀이 2
이중 for 문에서 해당 값이 0인지 확인하는 로직이 이미 있으므로 dfs에서 해당 값이 방문되었는지 확인하는 코드를 삭제하고, 큐에 해당 값이 있는지 확인 하는 코드를 추가해보았다.
사실 거의 똑같은 풀이..
graph = [
[1, 0, 0, 1, 1, 0],
[1, 1, 1, 1, 0, 0],
[0, 0, 1, 1, 1, 1],
[1, 0, 0, 1, 1, 0]
]
# 상하좌우
dx = [0, 0, -1, 1]
dy = [-1, 1, 0, 0]
from collections import deque
def bfs(startX, startY):
queue = deque([])
queue.append((startX, startY))
while queue:
currentX, currentY = queue.popleft()
graph[currentX][currentY] = 2 # 방문처리
for i in range(4): #(0,1)
nextX = dx[i] + currentX
nextY = dy[i] + currentY
if 0<=nextX<len(graph) and 0<=nextY<len(graph[0]):
if graph[nextX][nextY] == 0 and (nextX,nextY) not in queue:
queue.append((nextX,nextY))
def solution(s):
answer = 0
for row in range(len(s)):
for col in range(len(s[0])):
if s[row][col] == 0:
bfs(row, col)
answer += 1
return answer
solution(graph)bfs 함수
- dxdy : 좌 → 상 → 우 → 하
- sx, sy : 시작 노드 (위치)
- cx, cy : 현재 노드 (위치)
- nstX, nxtY : 이동할 노드 (위치)
- 방문한 그래프의 값은 0에서 2로 바꾼다.
큐를 사용하기 위해 빈 리스트에 deque를 선언했다. 탐색 전 시작 노드를 큐에 추가한다. 탐색은 큐가 빌 때까지 반복할 것이므로 `while dq` 안에서 bfs가 이루어진다.
[cx, cy] = dq.popleft()
우선 큐에서 노드 하나를 뽑아 현재 값으로 설정한다. 큐에는 방문 가능한 노드를 탐색한 결과가 담겨 있기에 큐에서 뽑음과 해당 위치를 그래프에서 방문처리한다. graph[cx][cy] == 2
for i in range(4)
현재 위치에서 dxdy로 탐색한다. 좌, 상 우, 하의 총 4개의 위치를 설정해두었으므로 반복문을 4번 돌린다.
각각의 위치의 방문 여부를 확인해야 하므로 nxtX, nxtY에 각각 현재 위치에서 dxdy 위치를 더한 값을 저장한다.
해당 위치가 인덱스를 벗어나는지 우선 판단한다. 벗어나지 않는다면 해당 위치의 그래프 내부의 값이 0인지를 확인하고 (방문한 0은 2로 값을 변경했음) 0이라면 큐에 이동할 위치를 저장한다. dq.append([nxtX, nxtY])
solution 함수
얼음틀의 개수는 answer에 저장된다. 따라서 초기값을 0으로 설정한다. bfs를 진행할 0을 찾는 과정으로 그래프 탐색을 위해 이중 for문을 활용한다.
해당 위치의 값이 0이라면 해당 위치를 넣어 bfs 함수를 호출한다. bfs 종료 후에는 answer 값을 하나 증가시킨다.


얼음
~~