2022-11-01
scikit-learn 기초 - fit & predict
이전 단계에서 예측하려는 특성(features)을 y, features를 예측할 때 사용하려는 특성(samples)을 X로 정의했다. 이 때 y를 모의하는 X 모델을 fitting 하는 방법은 아래와 같다. (이 강의에서는 데이터를 분류하는 모델 중 하나인 LinearSVC를 이용해 꽃을 분류하는 모델을 만든다.)
from sklearn.svm import LinearSVC
X = data[['petal length (cm)', 'petal width (cm)']] # 꽃의 특성(꽃잎 길이, 너비)
y = data[['target']] # 꽃의 종류
# Fit the model
model = LinearSVC()
model.fit(X, y)Why use double square brackets?
X,y를 할당할 때 두 개의 대괄호를 쓰는 이유는X,y의 데이터 타입이 pd.DataFrame이어야 하기 때문이다. 단일 대괄호를 쓰면 pd.Series가 되기 때문에 바깥쪽에 한 번 더 대괄호를 씌워 pd.DataFrame으로 만든다.
fitting한 모델을 이용해 새로운 samples X_predict의 features y_predict를 예측하는 방법은 아래와 같다.
X_predict = predict_data[['petal length (cm)', 'petal width (cm)']]
y_predict = model.predict(X_predict)이렇게 하면 y_predict에는 X_predict로 분류한 꽃의 종류가 array로 반환된다.
2022-11-03
오디오 데이터 처리
오디오 데이터(예: wav)는 librosa 패키지로 가공할 수 있다. 아래 코드는 y에 오디오 값(진폭)를 numpy array로 반환하고, sr에 초당 샘플수(아마도 주파수)를 반환한다.
import librosa as lr
audio, sfreq = lr.load(audio_files)
print(f'Shape of samples: {audio.shape}')
print(f'Number of samples: {audio[0]}')
print(f'Frequency: {sfreq} Hz')
print(f'Length of file: {audio.shape[0]/sfreq} sec')위 코드의 결과는 아래와 같다. 파일에는 총 174,980개의 오디오 진폭 값이 있고, 초당 22,050의 값이 있으며 파일의 전체 길이는 7.9초이다. audio의 채널이 여러 개인 경우에는 audio.shape의 값이 (첫 번째 채널의 값, 두 번째 채널의 값, ...) 이러한 형식으로 나온다.
Shape of samples: (174980,)
Number of samples: -0.006969843525439501
Frequency: 22050 Hz
Length of file: 7.935600907029478 sec오디오 진폭의 시계열을 그리려면 위 정보를 이용해 시간축 time array를 만들어 주면 된다.
# (위에 이어서)
# 위에서 구한 Length of time 까지의 배열을 만들어 시간축을 만든다. 채널이 하나이므로 audio.shape[0] 대신 len(audio)를 써도 된다.
time = np.arange(0, len(audio)) / sfreq
fig, ax = plt.subplots()
ax.plot(time, audio)
ax.set(xlabel='Time (s)', ylabel='Sound Amplitude')
plt.show()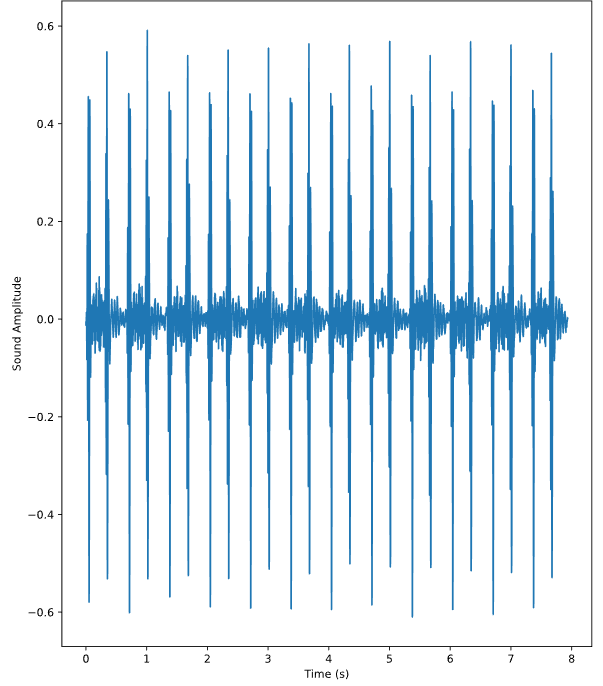
2022-11-05
subplots with for loop
보통 여러 개의 plot을 만들 때에는 fig, axs = plt.subplots(2, 2)와 같이 subplot을 생성한다. 만약 data_set이라는 np.array 안에 plot을 만드려는 np.array가 있다고 가정하다(즉 data_set = [[a, b, c...], [A, B, C...], ...])) 이 때 각 ax에 loop를 이용해서 그림을 그리는 방법은 아래와 같다.
fig, axs = plt.subplots(3, 2)
for each_data, ax in zip(data_set, axs.T.ravel()):
ax.plot(x_axis, each_data)이 때 axs.T.ravel()은 axs에 loop를 사용할 수 있도록 subplot 행렬을 1차원 array로 변환해준다.
이해를 돕기 위해서 axs, axs.T, axs.T.ravel()의 모양을 확인하면 다음과 같다.
'''
axs
[[0 1]
[2 3]
[4 5]]
'''
[[<AxesSubplot:> <AxesSubplot:>]
[<AxesSubplot:> <AxesSubplot:>]
[<AxesSubplot:> <AxesSubplot:>]]
'''
axs.T
[[0 2 4]
[1 3 5]]
'''
[[<AxesSubplot:> <AxesSubplot:> <AxesSubplot:>]
[<AxesSubplot:> <AxesSubplot:> <AxesSubplot:>]]
'''
axs.T.ravel()
[0 2 4 1 3 5]
'''
[<AxesSubplot:> <AxesSubplot:> <AxesSubplot:> <AxesSubplot:>
<AxesSubplot:> <AxesSubplot:>]여기에서는 0 → 2 → 4 → 1 → ... 즉 좌측 subplot을 먼저 채우고 우측 subplot을 그리기 위해서 이렇게 한 것이다. 용도에 따라서 적절히 reshape한 다음 ravle()하면 된다.
Classifying a times series
noise가 많은 시계열을 머신러닝에 사용할 때에는 시계열 원본보다 시계열의 특성(진폭의 평균, 최대, 최소 등)을 이용하는 것이 유리할 수도 있다.
예를 들어 복수 개의 시계열 set인 data_set을 가지고 있다면 다음과 같이 moving average로 각 시계열의 노이즈를 줄인 뒤에 각 시계열의 평균, 표준편차, 최대값 등을 예측에 사용할 수 있다.
'''
data_set
1 2 3 4 5 6
time
0.000e+00 -9.952e-04 2.808e-04 2.953e-03 0.005 4.332e-04 1.316e-03
4.535e-04 -3.381e-03 3.808e-04 3.034e-03 0.010 5.541e-04 -1.535e-04
... ... ... ... ... ... ...
3.998e+00 -8.946e-05 -5.931e-03 2.474e-03 0.008 3.157e-04 -6.354e-03
3.998e+00 -1.119e-04 -4.839e-03 4.467e-03 0.008 -2.686e-04 -1.067e-02
'''
data_smooth = data_set.rolling(window = 10)
data_mean = np.mean(data_set, axis=1)
data_stds = np.std(data_set, axis=1)
data_max = np.max(data_set, axis=1)
X = np.column_stack([means, stds, maxs])
y = labels.reshape(-1, 1)단순 교차 검증
참고: 블로그
일반적으로 머신러닝 성능을 측정할 때 학습셋과 예측셋(테스트셋)을 X_train, X_test, y_train, y_test로 나누어 확인한다.
다만 반복적으로 X_train을 이용해 학습을 시킬 경우 모델이 학습셋에 과적합될 위험이 있다. 이를 해결하기 위해 나온 방법이 '교차 검증'이다.
학습셋 전체를 사용하는 대신 학습셋을 임의의 k개로 나누어 '폴드'를 만든다. 이 중 하나의 폴드를 예측셋으로 사용하고 나머지를 학습셋으로 사용하면서 총 k 개의 모델을 생성한다. 이 때 각 모델의 정확도를 측정할 때 사용하는 매소드가 cross_val_score이다.
cross_val_score(model, sample, feature)의 형식으로 사용하고 몇 개의 폴드를 만들 것인지 결정하는 cv를 선택 인자로 받는다. 예시는 다음과 같다.
from sklearn.model_selection import cross_val_score
model = LinearSVC()
scores = cross_val_score(model, X, y, cv=3)
print(scores)
# [0.66666667 0.75 0.83333333 0.83333333 0.5]2022-11-06
Spectogram (Short Time Fourier Transform)
출처: 블로그
Spectogram은 (오디오) 시계열을 window 사이즈로 지나가면서 각 구간을 Foureir 변환 한 것을 말한다. 시계열 전체를 하지 않고 window 사이즈만큼 하는 이유는 오디오 신호가 긴 구간에서는 상대적으로 non-stationary, 짧은 구간에서는 stationary하다고 보기 때문이다.
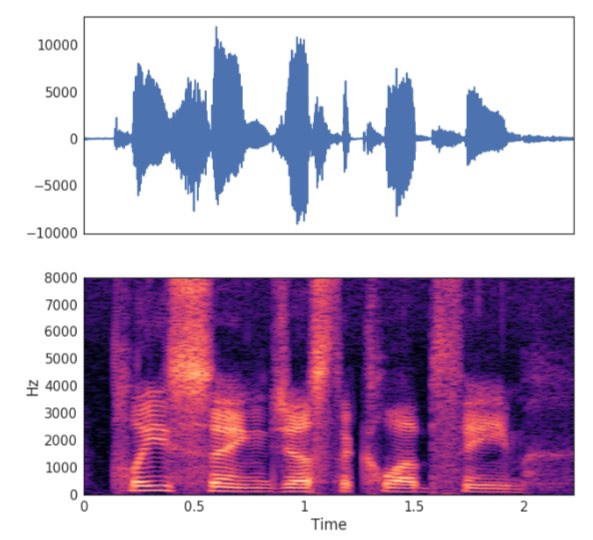
출처: DataCamp
여기서 가로축은 시간(window 구간), 세로축은 Fourier 변환 주파수, z축은 Fourier 변환 진폭을 의미한다. 즉 짙은 색으로 갈수록 해당 구간에서 해당 주파수를 가지는 sin/cos 파의 진폭이 크다는 의미이다.
stft는 Spectogram을 반환하는 매소드이다. 그 결과는 specshow를 통해 가시화할 수 있다.
from librosa.core import stft, amplitude_to_db
from librosa.display import specshow
import matplotlib.pyplot as plt
HOP_LENGTH = 2**4
SIZE_WINDOW = 2**7
audio_spec = stft(audio, hop_length=HOP_LENGTH, n_fft=SIZE_WINDOW)
# 스펙토그램을 dB 스케일로 변환
spec_db = amplitude_to_db(audio_spec)
fig, axs = plt.subplots(2, 1, figsize=(10, 10), sharex=True)
axs[0].plot(time, audio)
specshow(spec_db, sr=sfreq, x_axis='time', y_axis='hz', hop_length=HOP_LENGTH, ax=axs[1])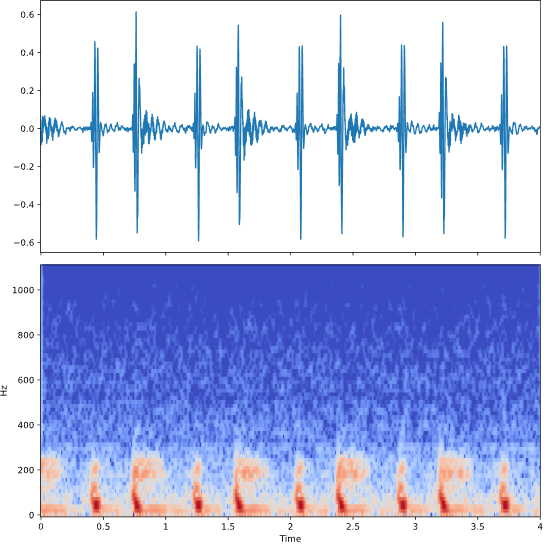
Machine Learning with spectral features
이전에는 오디오의 평균값 등을 LinearSVC 모델의 sample로 사용했다. 이제 앞에서 배운 Spectrogram과 spectral features를 사용해서 sample 특성을 추가할 수 있다.
# (이전 코드에 이어서)
bandwidths = []
centroids = []
# Spectral Bandwith, Spectral Centroid 추출
for spec in spectrograms:
this_mean_bandwidth = np.mean(lr.feature.spectral_bandwidth(S=spec))
this_mean_centroid = np.mean(lr.feature.spectral_centroid(S=spec))
# Collect the values
bandwidths.append(this_mean_bandwidth)
centroids.append(this_mean_centroid)
X = np.column_stack([means, stds, maxs, tempo_mean, tempo_max, tempo_std, bandwidths, centroids])
y = labels.reshape(-1, 1)
from sklearn.model_selection import cross_val_score
model = LinearSVC()
percent_score = cross_val_score(model, X, y, cv=5)
print(np.mean(percent_score))2022-11-12
하... 코로나 막차 타는 중 😷 지독하구만!
pd.DataFrame Scatter plot
index에 따라서 산점도의 색이 바뀌는 scatter plot을 그리려면 인수 c에 index array를 주면 된다.
df.plot.scatter('col1', 'col2', c=df.index, cmap=plt.cm.viridis)interpolation type
scipy.interpolate(data_array)는 kind 인수를 받는다. kind는 어떤 방식으로 interpolate 할 것인지를 정한다. 자세한 종류는 문서 참조.
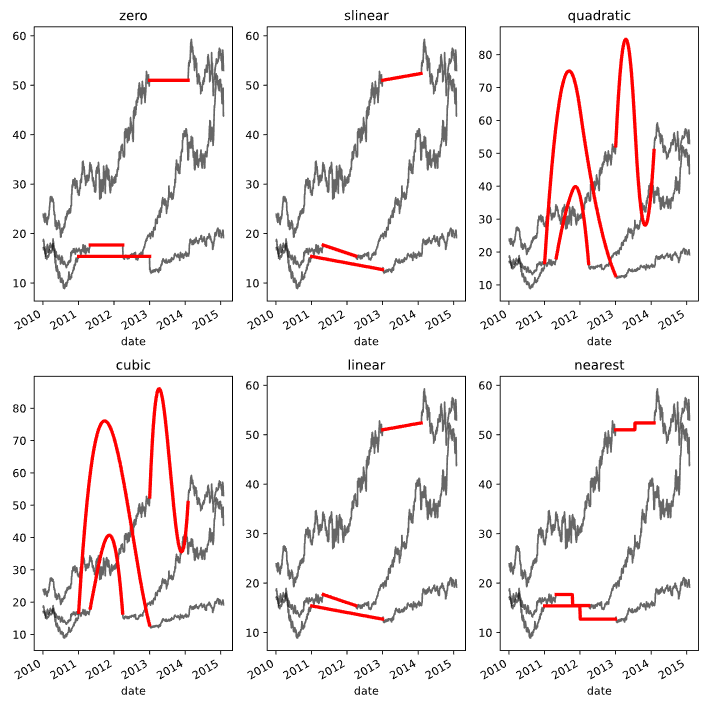
zero, slinear, quadratic, cubic은 각자 0~3차 Spline interpolation을 가리킨다. Spline interpolation이란 고차항의 Polynomial interpolation을 사용하는 대신 데이터를 특정 개수의 구간으로 분해해서 각 구간을 0~3차 다항식에 맞추는 방식을 말한다. 이해를 잘 못 하겠지만... 모든 데이터를 하나의 고차 다항식에 맞추면 일종의 과적합과 유사한 문제가 발생하기 때문에, 이 문제를 해소하기 위한 interpolation 방법이라는 정도까지만 이해했다(출처: 블로그).
2022-11-13
Cross-Validating time series data
ShuffleSplit 교차검증은 시계열 데이터에는 적합하지 않다. 시계열은 문자 그대로 시간에 상관이 있는데, 아래처럼 무작위로 나눈 chunk(fold)는 시간 정보를 모두 삭제하기 때문이다. 이 두 가지 방법은 각 데이터셋이 독립적으로 분포할 때에 적합한 방법이다. KFold 교차검증의 경우 한 fold 내에서 데이터의 시계 정보가 어느 정도 남아있으나 미래와 과거 fold가 뒤섞일 수 있으므로 좋은 방법은 아니다.
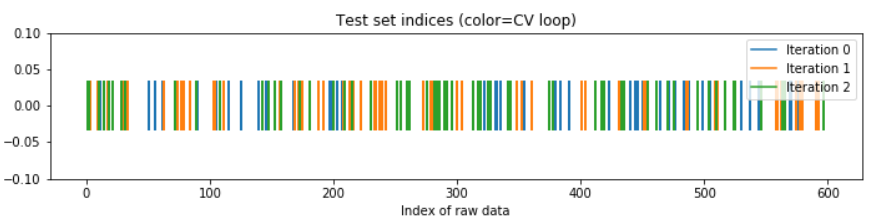
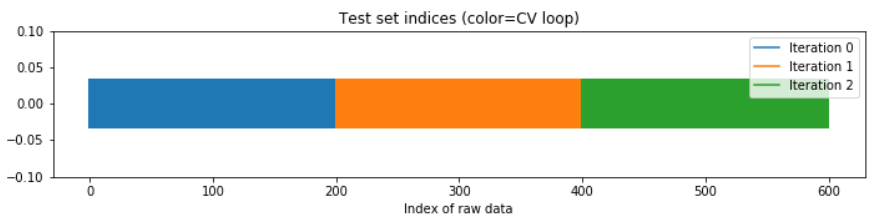
위: KFold, 아래: ShuffleSplit
출처: DataCamp
시계열을 ShuffleSplit 으로 교차검증할 경우, 아래와 같이 데이터 포인트의 시간에 따른 순서가 모두 사라지고 섞인 상태로 교차검증을 수행한다.
# Import ShuffleSplit and create the cross-validation object
from sklearn.model_selection import ShuffleSplit
cv = ShuffleSplit(n_splits=10, random_state=1)
# Iterate through CV splits
results = []
for tr, tt in cv.split(X, y):
# Fit the model on training data
model.fit(X[tr], y[tr])
# Generate predictions on the test data, score the predictions, and collect
prediction = model.predict(X[tt])
score = r2_score(y[tt], prediction)
results.append((prediction, score, tt))
# Custom function to quickly visualize predictions
visualize_predictions(results)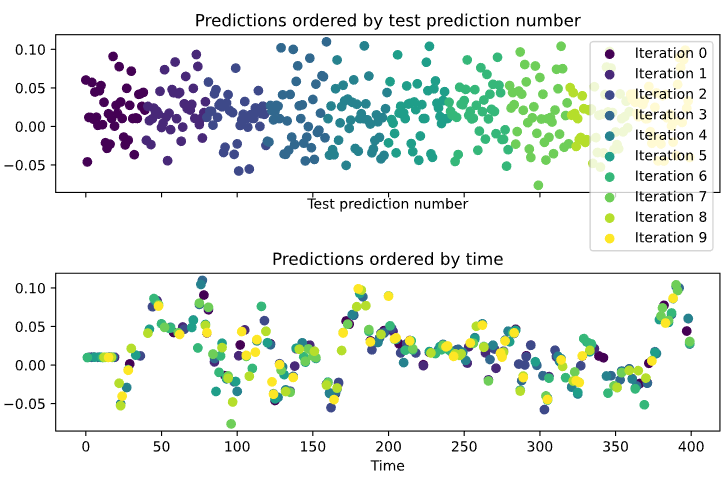
시계열을 예측할 때에는 '과거'의 정보를 사용해 '미래'의 정보를 예측해야 한다. 이 조건을 만족하는 교차검증이 TimeSeriesSplit 이다. (팜유 예측할 때 썼던 거군) 이 교차검증은 아래와 같은 iteration을 돌면서 과거(파란색) 데이터를 이용해 미래(빨간색)을 예측하고 그 성능을 반환한다.
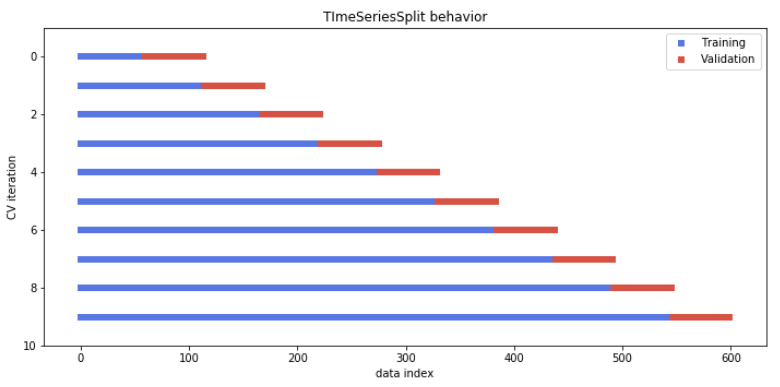
출처: DataCamp
Stationarity and Model Stability
대부분의 모델에는 input과 output의 관계가 static하다는 가정이 깔려있다. 만약 데이터가 stationary하지 않다면 시간에 따라 둘의 관계가 static하지 않을 수 있다. 이를 확인하기 위한 방법 중 하나가 교차검증이다. 교차검증을 통해 나온 모델의 계수(coeff)가 교차 세트마다 크게 달라진다면 데이터가 non-stationary하다고 유추할 수 있다.
TimeSeriesSplit을 이용해 cross_val_score을 구한 것을 교차 세트에 따라 plot한 결과가 아래와 같다면, score가 크게 변하는 구간을 통해 데이터가 non-stationary함을 유추할 수 있다.
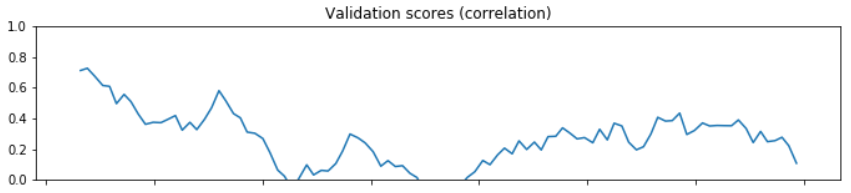
2022-11-14
Bootstrapping
Bootstrap은 늪에 빠진 사람이 자기 자신의 부츠 끈(bootstrap)을 끌어잡아 올렸다는(뉴턴역학을 어떻게 한 건지 알 수 없는) 이야기에서 나왔다고 한다. 중요한 점은 '자기 자신'의 끈이다. 하나의 샘플이 존재할 때, 중복을 허용해서 똑같은 개수의 데이터를 뽑아 새로운 샘플을 만들어낸다. 이걸 여러 번 반복해서 자기 자신으로부터 나온 여러 개의 샘플을 뽑아 estimator(추정량)의 분포를 확인하는 작업을 Bootstrap이라고 한다.
여기서 estimator은 평균, 중위값... 등의 표본을 이용해서 계산하는 일종의 통계치라고 보면 된다
이걸 왜 하나
표준 오차가 알려지지 않은 estimator의 표준 오차를 구하기 위함이다. 샘플의 estimator을 구하면 우리는 그 estimator가 모집단의 estimator와 다르다는 사실을 알고 있다. 모집단으로부터 어떤 샘플을 꺼내느냐에 따라 estimator의 값은 조금씩 변할 것이다. 그래서 우리는 샘플의 estimator가 가지는 값의 범위와 표준 오차를 파악한다. 다만 특정 estimator의 표준 오차는 잘 알려져 있지만(예: 평균) 표준 오차가 알려지지 않은 estimator도 있다(임의로 만든 통계치도 포함해서). 이러한 estimator의 표준 오차를 알아내기 위해, Bootstrap으로 여러 개의 샘플을 만들어 낸 후 그 샘플들로부터 estimator의 분포와 표준 오차를 구하는 것이다.
2022-11-16
이제 스터디는 끝났고, 지금부터는 뭘 공부할지 다시 정하면 된다!
일단은 ARIMA 강의를 들어봐야지~ (이 강의가 다른 강의에 비해 설명이 좀 더 구체적인 듯!)
Stationarity 정의 (자세히)
정상성을 가지려면 아래 세 가지 조건을 만족해야 한다.
- 추세가 없어야 한다(Trend is zero).
- 데이터의 분산이 시간에 따라 변하지 않아야 한다(Variance is constant).
- 자기상관이 시간에 따라 변하지 않아야 한다(Autocorrelation is constant).
Stationarity Test with Dicky-Fuller Test (자세히)
귀무 가설: 시계열이 (추세 관점에서) non-stationary 하다.
from statsmodels.tsa.stattools import adfuller
results = adfuller(time_series_df['data_column'])
print(results)
# (-1.34, 0.60, 23, 1235, {'1%': -3.435, '5%': -2.913, '10%': -2.568}, 10782.87)returns의 첫 번째 값(test statistic)이 음수일수록 시계열이 stationary할 가능성이 높다. (3번과 결합하면 그 가능성의 정도를 파악할 수 있다)returns의 두 번째 값은 p-value이다. p-value가 threshold 미만이면 귀무 가설을 잘못 기각하였을 가능성이 낮다. 즉 귀무 가설을 기각하여 시계열이 stationary하다는 대립 가설을 채택할 수 있다.returns의 마지막 딕셔너리는 p-value에 해당하는 임계값을 보여준다. 1번 값을 임계값과 비교할 수 있다.
단, 앞서 귀무 가설에 기재한대로 Dicky-Fuller test는 '추세'에 관하여서만 정상성을 확인한다. 예를 들어 아래의 데이터는 실제로는 non-stationary이지만, Dicky-Fuller test는 추세만을 확인하므로 귀무 가설을 기각한다(시계열이 stationary하다고 판단한다).
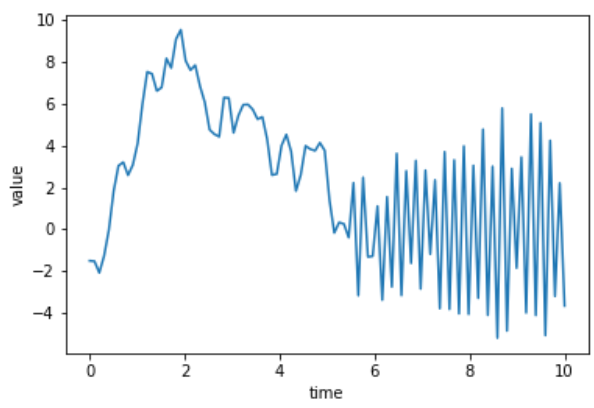
출처: DataCamp
2022-11-21
ARMA Model (자세히)
앞서 본 AR Model과 MA Model을 합친 것이 ARMA Model이다. (이론적인 설명은 더 나오지는 않는다...) 다시 한 번 복습하면 ARMA Model 수식은 다음과 같다.
여기서 가 AR Model 차수, 가 MA Model 차수이다.
지정한 AR, MA parameter을 이용해 ARMA Model을 생성하는 코드는 아래와 같다.
이 때 AR, MA parameter은 차수에 따라 list를 받으며 [1, -ar1, -ar2, ...], [1, ma1, ma2, ...] 와 같이 설정한다. 맨 처음 1은 0차항의 parameter이기 때문에 AR 혹은 MA 차수가 없다 하더라도 반드시 1로 설정해야 한다. (그래야 가 존재하니까) AR parameter은 음수로 받는 것도 주의한다.
from statsmodels.tsa.arima_process import arma_generate_sample
# MA(1), MA 1차 parameter가 -0.7인 경우
ar_coefs = [1]
ma_coefs = [1, -0.7]
# nsamples; 정수인 경우 1-D의 해당 길이의 시계열 생성, 튜플인 경우 해당 길이의 차원 시계열 생성
# scale; noise(epsilon)의 표준편차
y = arma_generate_sample(ar_coefs, ma_coefs, nsample=100, scale=0.5)
plt.plot(y)
plt.show()2022-11-22
어쩐지 맘에 드는 일자로구만
ARMAX Model Fitting
이전에 ARIMA 패키지를 이용해서 데이터를 AR(I)MA Model에 fitting하는 방법을 배웠다. 여기에서는 의 ARMA에 외부인자 를 추가해서 ARMAX fitting하는 방법을 다룬다.
끝에 붙는 'X'는 외부인자를 가리킨다. 즉 ARMAX는 ARMA에 linear regression을 합친 것과 같다.
ARIMA 패키지를 이용해 ARMAX Model에 fitting하는 코드는 다음과 같다. exog parameter에 외부인자 데이터를 주어 ARMAX에 fitting할 수 있다.
# ARMA(2,1) 사용하는 경우
model = ARIMA(my_df['data'], order=(2,0,1), exog=my_df['external_data'])
results = model.fit()
print(results.summary())2022-11-23
DataCamp가 갑자기 멈춰서 🙄 오늘 처음 써 본 python decorator 정리!
decorator
내가 이해한 decorator의 기능은 f(g(x))에서 f(x)이다. 즉 함수 자체를 인자로 받는 함수를 만들어야 할 때 쓰는 것.
f(g(x))를 한 번만 쓸거라면 굳이 decorator을 쓸 필요가 없을 수도 있지만, f(g(x)) 말고도 f(h(x)), f(l(x))...와 같이 여러 함수를 인자로 넘기는 경우라면 decorator을 쓰는 게 편리하다.
decorator의 가장 좋은 예시가 '각 함수를 실행할 때마다 소요되는 시간을 알려주는 타이머'이다. 보통은 함수를 시작할 때 start_time = time.time()로 시작시각을 기록하고, 함수가 끝날 때 time.time() - start_time과 같이 종료시각과 시작시각의 차이를 보여주는 방식으로 소요 시간을 측정한다.
그런데 모든 함수에서 소요 시간을 측정해야 한다면 저 구문을 매번 넣어주는 방식이 비효율적이다. 이 때 사용하는 것이 decorator이다.
decorator을 class로 만드는 방법도 있고, 함수로 만드는 방법도 있는데 나는 후자의 방법을 선택했다(관리의 용이성을 고려하면 전자가 더 나을 수도 있다. 상황에 맞게 방법을 택하면 될 듯).
시간을 측정하는 함수인 timer를 다음과 같이 정의한다.
import time
def timer(inner_func):
def wrapper_func(*args, **kwargs):
start_time = time.time()
result = inner_func(*args, **kwargs)
end_time = time.time()
print(f"Takes {end_time-start_time} sec")
return result
return wrapper_func여기서 timer은 함수 자체(inner_func)를 인자로 받는다. timer 내부의 wrapper_func은 위에서 f(x)의 역할을 하는데, f(x)의 내부에서 result = inner_func()을 이용해 g(x)를 실행한다. 즉 start_time을 기록하고, result로 inner_func을 실행한다. 실행이 끝나면 다시 end_time을 기록해서 실행 시간을 출력하는 방식이다.
이 함수를 decorator로 실제 함수에 적용하는 방식은 아래와 같다.
@timer
def my_func():
print("Hello world")
return None이렇게 하면 timer의 인자로 my_func이 들어가면서 위의 절차대로 실행 시간을 출력한다.
다만 굳이 timer 안에 wrapper_func을 추가로 정의하는 이유는 아직 완벽히 이해를 못했다. 찾아보니 Closer에 대해서도 좀 더 알아봐야 할 것 같다. 내일 읽어봐야겠다.
2022-11-24
왜 decorator 안에 wrapper을 정의하나?
나랑 같은 의문을 가진 게시글이 하나 있었다. 왜 decorator 안에 굳이 wrapper 함수를 추가하는지 모르겠다는 질문. 어제 본 timer을 예시로 들면 다음과 같다.
# wrapper가 있는 decorator(원본)
def timer(inner_func):
def wrapper_func(*args, **kwargs):
start_time = time.time()
result = inner_func(*args, **kwargs)
end_time = time.time()
print(f"Takes {end_time-start_time} sec")
return result
return wrapper_func
# wrapper가 없는 decorator
def timer(inner_func):
start_time = time.time()
result = inner_func(*args, **kwargs)
end_time = time.time()
print(f"Takes {end_time-start_time} sec")
return None위든 아래이든 result에서 inner_func을 불러오는 동작은 똑같은데 왜 굳이 wrapper_func 구간이 필요한지 이해가 가지 않았다.
여기에 대한 답변은 다음과 같다.
decorator는 결국 timer(inner_func)을 실행하는 것이다.inner_func이 특정 값을 return하는 경우를 가정해보자.
@timer
def my_func():
return "Hello"
my_value = my_func()
# my_value = timer(my_func)여기서 my_value = my_func()은 결국 timer(my_func)과 같다. 이 때 timer 안에 wrapper 함수가 없으면 timer는 None을 반환하기 때문에(위의 timer 함수 정의 참고), timer(my_func)은 내부의 값이 무엇이 되었든 항상 None을 반환한다. 즉 my_value는 "Hello"가 아니라 None이 된다.
이 때문에 decorator 안에 wrapper 함수를 정의한다고 설명한다.
갑자기 든 의문
그러면 이렇게 정의하면 return 값을 "Hello"로 받을 수 있지 않나? 결국 wrapper을 사용했을 때에도 wrapper에서result를 반환하고 다시 decorator가wrapper_func을 반환하는 거라면... 테스트를 해봐야겠다.def decorator_func(inner_func): # do something result = inner_func(*args, **kwargs) # do something return result
result랑wrapper_func이랑 다른 것이라면 wrapper을 쓰는 이유를 납득할 수 있다.
