12월 TIL

Soo Im·2022년 12월 13일

Data Analysis TIL python

일별 TIL 기록

목록 보기

15/21

테스트로 야근하는 나날... 언젠가 끝나겠지? 🥺 매일은 어려워도 회사에서 쓴 거라도 적어보자
(저번 달에 못다한 ARIMA랑 wrapper도 잊지말자...)

2022-12-13

Python multiple returns in map for DataFrame

나의 상황: 여러 개의 값을 반환하는 함수를 pd.DataFrame 의 특정 열에 map으로 실행해서, 그 결과 값을 각각 열로 추가하고 싶다.
(해결법은 맨 밑에!)

온라인에 나온 해결법:

여러 개의 값을 반환하는 함수에서 반환값을 각각 받는 법 자체는 많다. 아래는 대표적인 예시 두 가지.

# 1번: 반환값 개수대로 변수 선언하기
def my_func():
	...
	return "hello", "world"
r1, r2 = my_func()
# print(r1) -> "hello"
# print(r2) ->  "world"

# 2번: 반환값을 list로 묶어 반환하기
def my_func():
	...
	return ["hello", "world"]
r1 = my_func()
# print(r1) -> ["hello", "world"]

map을 이용하는 경우에는 반환값이 map object로 나오기 때문에 약간의 가공이 필요하다. 참고한 링크1(map object), 링크2(multiple returns with map).

def function(x):
    return x, x+1
    
sequence = range(5)

print("map object")
print(map(function, sequence))

print("\nelements in map object")
for i in map(function, sequence): print(i)

print("\nlist")
print(list(map(function, sequence)))

/*출력 결과*/

map object
<map object at 0x7f504ad91370>

/*map은 map object를 반환하기 때문에 각 element를 직접 출력해야 내부의 값을 볼 수 있다.*/
elements in map object
(0, 1)
(1, 2)
(2, 3)
(3, 4)
(4, 5)

/*map object를 list나 tuple로 변환하면 다음과 같이 나온다.*/
list
[(0, 1), (1, 2), (2, 3), (3, 4), (4, 5)]

위에서 첫번째 반환값과 두 번째 반환값을 각각 묶고 싶다면 내장 함수인 zip을 사용하면 된다. zip은 길이가 같은 여러 개의 iterable 변수를 index 기준으로 묶어서 출력해주는 함수이다.

print("\nzip")
a = zip(*map(function, sequence))
for i in a: print(i)

/*map object 내부의 (0,1) (1,2)..을 index 기준으로 묶어서 출력한다.*/
zip(0, 1, 2, 3, 4)
(1, 2, 3, 4, 5)

나의 해결법:

df['col1'].map(lambda x: my_func(x))와 같이 특정 DataFrame에 실행해서 그 결과를 df['col2'], df['col3']로 추가하는 방법은 아래와 같다.

# multiple return을 list로 묶어서 반환
def my_func():
	...
	return [r1, r2]

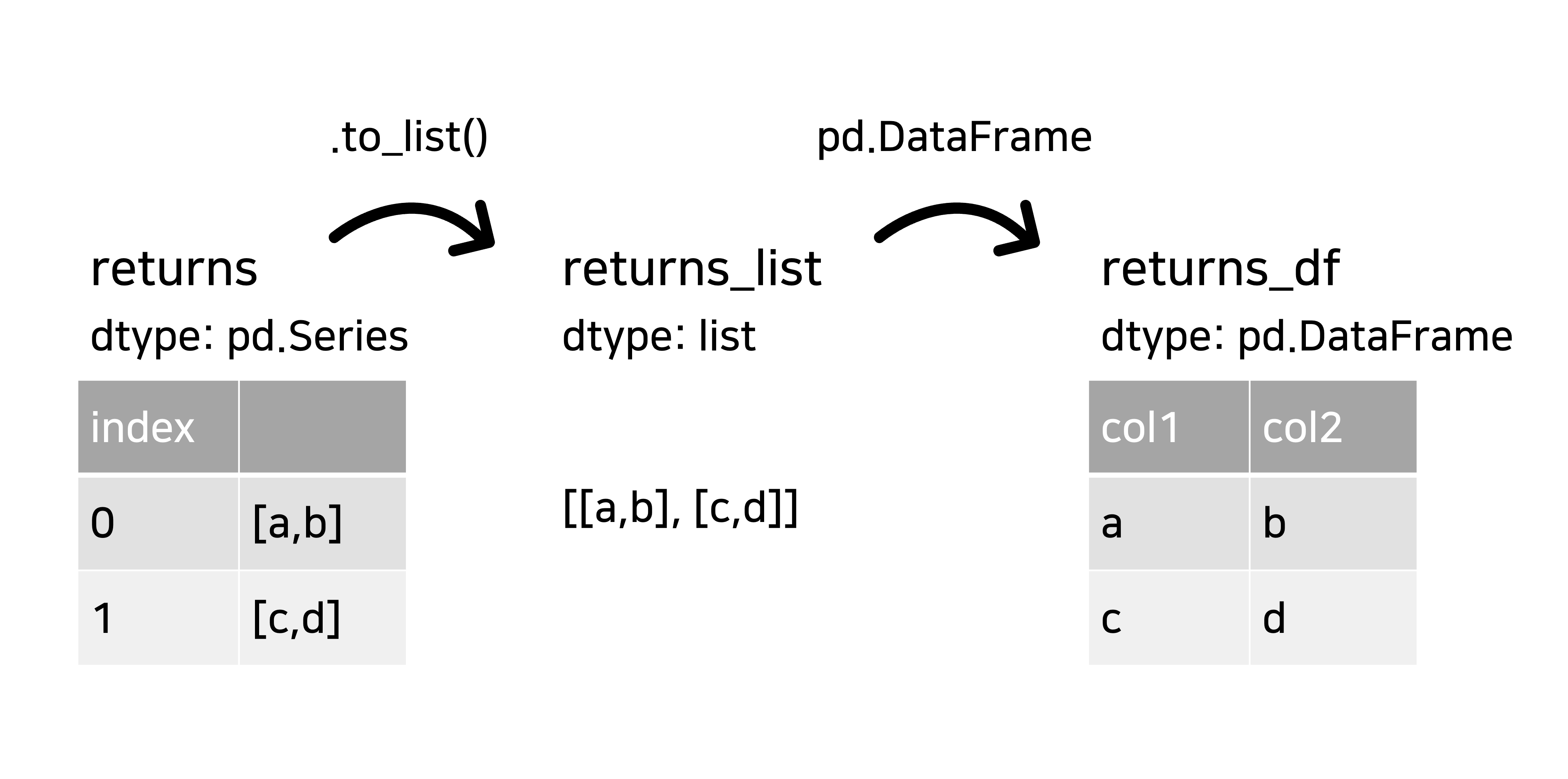
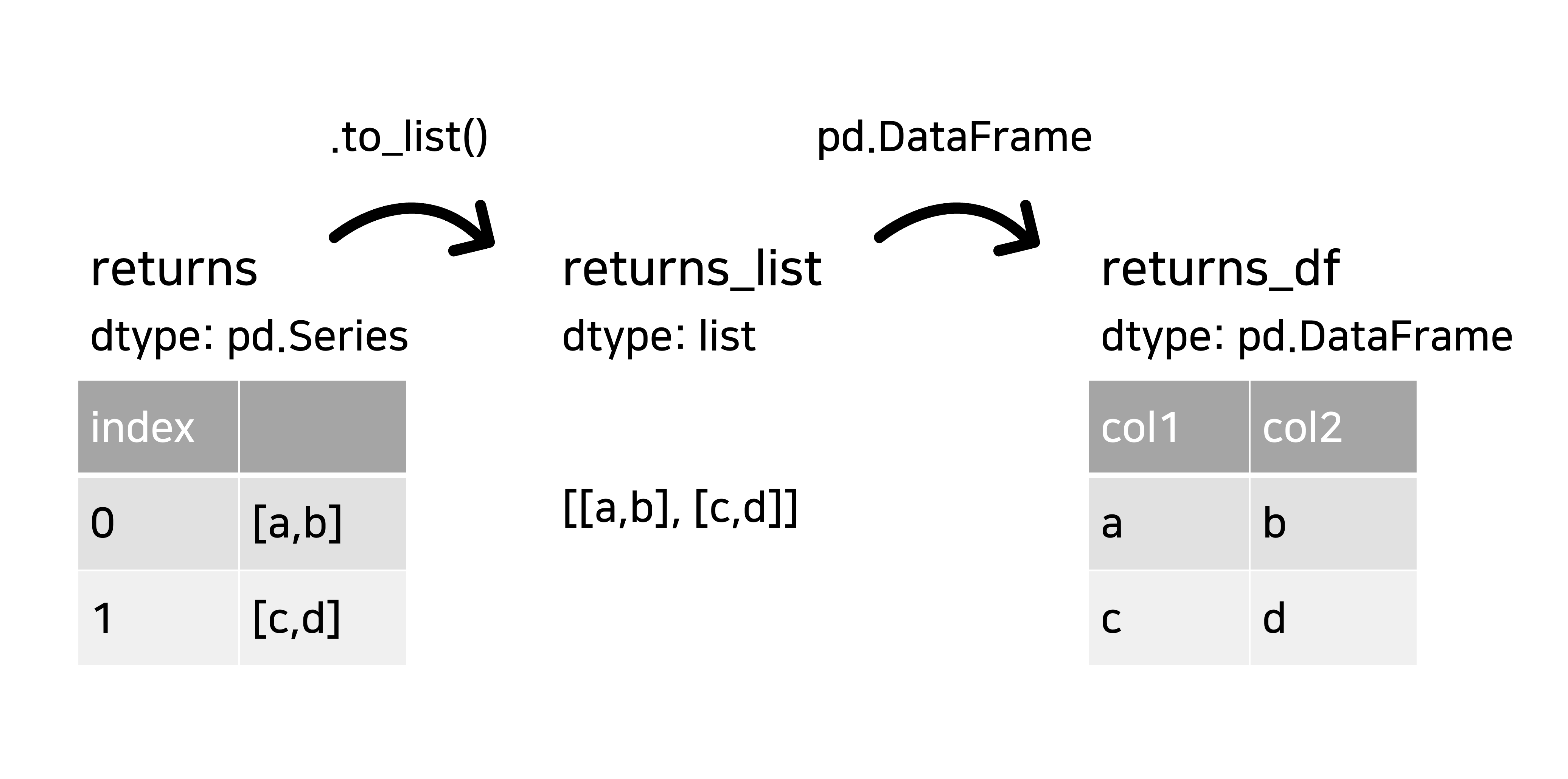
returns = df['col1'].map(lambda x: my_func(x))
returns_df = pd.DataFrame(returns.to_list(), columns=['col2', 'col3'])

df['col2'] = returns_df['col2']

(쓰고 나니 뭔가 최선의 방법은 아닌 것 같지만...)

returns는 map object가 아니라, 각 행별로 실행한 반환값 list를(예:[0,1]) 각 index마다 가지는 pd.Series가 된다.
나는 각 index 내부의 list를 DataFrame으로 변환하고 싶기 때문에, pd.Series를 to_list()를 이용해 먼저 nested list로 바꾸어주었다([[0,1],[1,2],...]) 그리고 nested list에 pd.DataFrame을 사용해서 복수 개의 return 값을 각각의 열로 가지는 DataFrame을 만들 수 있다.

2022-12-15

왜 decorator 안에 wrapper을 정의하나? (2)

지난 달 게시글에서 가졌던 의문 이어서~

아래는 wrapper을 써야 하는 이유를 보여주는 코드이다. 두 번째의 "wrapper가 없는 decorator" 코드를 보고 '그러면 아예 return 자체를 result로 하면 되는 것 아니야?' 라고 생각했다.

# wrapper가 있는 decorator(원본)
def timer(inner_func):
    def wrapper_func(*args, **kwargs):
        start_time = time.time()
        result = inner_func(*args, **kwargs)
        end_time = time.time()
        print(f"Takes {end_time-start_time} sec")
        return result
    return wrapper_func

# wrapper가 없는 decorator
def timer(inner_func):
    start_time = time.time()
    result = inner_func(*args, **kwargs)
    end_time = time.time()
    print(f"Takes {end_time-start_time} sec")
    return None

# 그럼 이렇게 하면? 이라는 의문이 드러난 코드
def decorator_func(inner_func):
    # do something
    result = inner_func(*args, **kwargs)
    # do something
    return result

결론을 말하면 마지막은 물론이고 "wrapper가 없는 decorator" 코드도 동작하지 않는다. 코드 실행 결과는 아래와 같다.

Traceback (most recent call last):
  File "<string>", line 11, in <module>
File "<string>", line 5, in timer
NameError: name 'args' is not defined

inner_func에 넘겨준 인자 args가 정의되지 않았다고 나온다.

음... 이유를 계속 추측해 보려고 하는데, 완벽히 이해가 가지는 않는다. timer(inner_func)이기 때문에, inner_func에 넘겨줄 args가 함수 내부에서 정의되지 않았다는 건 이해가 간다. 그런데 그걸 wrapper_func의 인자로 정의한 것 만으로도 해결이 된다는게 좀 의문이다.
wrapper_func에서 임의의 arg를 받아온다고 가정하면 그게 곧바로 inner_func으로 전달되는 형식인데. wrapper_func은 어떻게 my_value = inner_func(*args) 이런 식으로 호출한 inner_func의 인자를 직접 받아오는 건지 이해가 잘 안 간다.

이런저런 자료를 많이 찾아보았지만 정확히 이 의문에 대한 답은 찾을 수가 없어서... 'inner_func에 넘겨야 할 args가 정의되지 않았기 때문에 wrapper가 존재해야 한다'로만 이해하고 넘어가야겠다. 🙁

2022-12-18

ARIMA Forecasting

10월 강의는 ARIMA forecasting 파트에서 예측값을 plot만 하는 방법만 제시했지만

from statsmodels.tsa.arima.model import ARIMA
from statsmodels.graphics.tsaplots import plot_predict

model = ARIMA(data, order=[1, 0, 0]) # 1차 AR
resesult = modelfit()

fig, ax = plt.subplots()
plot_predict(resesult, start=1000, end=1010, ax=ax) # 모델로 예측한 데이터 플롯

이번 강의는 예측값과 오차범위를 pd.DataFrame으로 얻는 방법을 소개한다.

In-sample prediction

fitting에 사용한 데이터 sample(여기서는 data) 내부에서 예측하는 방법이다. 2022-01-01~2022-12-31의 index를 가진 data에 ARIMA 모델을 fitting을 했다고 가정하자. 그 모델을 이용해 다시 2022-12-01부터 2022-12-31까지 마지막 30일간을 예측하려고 한다. 2022-12-01의 값은 data의 11-31을 이용해 예측하고, 12-02의 값은 data의 12-01 값을 이용해 예측하고... 한 step 이전의 데이터 sample data를 이용해 예측하는 방식을 In-sample prediction이라고 한다.

from statsmodels.tsa.arima.model import ARIMA

# fitting 단계까지는 위와 동일
model = ARIMA(data, order=[1, 0, 0])
resesult = model.fit()

# 이전 단계의 data sample 이용해 예측
forecast = results.get_prediction(start=-30)

get_prediction의 start 인자는 데이터 sample의 index 시작점을 가리킨다. start='2022-12-01'로 두어도 동일한 결과를 얻을 수 있다.

예측 결과 object forecast는 예측의 중앙값과 오차항( $\epsilon_t$ )으로 인한 confidence range를 가지고 있다. 각각은 .predicted_mean과 conf_int()를 이용해 얻을 수 있다.
기존 데이터와 in-sample 예측값, 그리고 예측의 오차범위를 얻고 plot하는 방법은 아래와 같다.

# 예측 중앙값
mean_forecast = forecast.predicted_mean
# 예측 오차범위
confidence_intervals = forecast.conf_int()
lower_limits = confidence_intervals.loc[:,'lower close']
upper_limits = confidence_intervals.loc[:,'upper close']

# data와 예측값 plot
plt.plot(data.index, data, label='observed')
plt.plot(mean_forcast.index, mean_forcast.values)
plt.fill_between(lower_limits.index, lower_limits, upper_limits)
plt.show()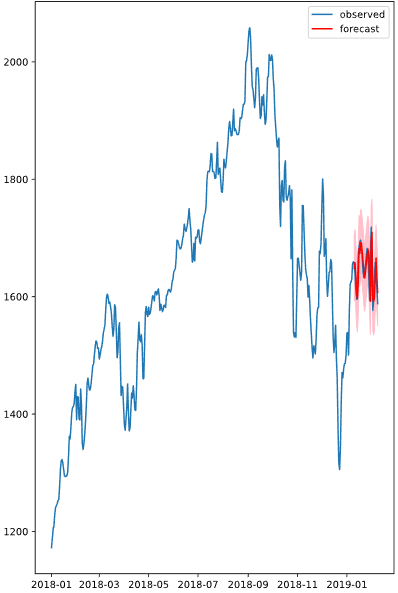

ARIMA_in-sample_prediction_with_confidence_interval

Dynamic prediction

In-sample과 달리 데이터 sample data가 아니라, 예측한 값에 이어서 다음 단계를 예측하는 방식을 Dynamic prediction이라고 한다. 예측값에 계속해서 오차( $\epsilon_t$ )가 더해지기 때문에 단계를 거듭할수록 오차 범위도 점점 커진다.

예측 방법은 위의 코드에서 dynamic 인자만 추가하면 된다.

# 이전 단계의 prediction 이용해 예측
forecast = results.get_prediction(start=-30, dynamic=True)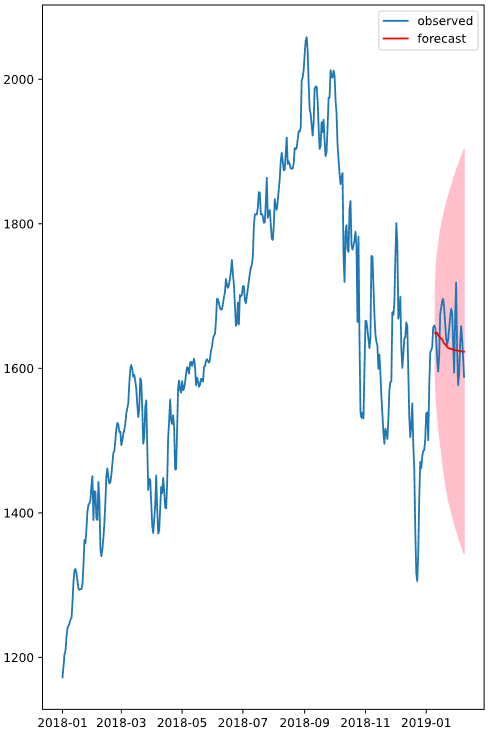

ARIMA_dynamic_prediction_with_confidence_interval

2022-12-21

ARIMA

ARIMA는 비정상성(non-stationarity)을 가지는 시계열에 대한 ARMA 예측을 돕는 패키지이다.

비정상성을 가지는 시계열 $X_t$ 을 ARMA 예측한다고 가정해보자. ARMA는 정상성을 전제로 하기 때문에, $X_t$ 를 그대로 사용하는 대신 n차 차분(differencing)을 취해야 한다.
차분을 취한 시계열 $X_{t}'$ 에 대해 ARMA 예측을 하면 그 결과는 $X_t$ 가 아닌 $X_{t}'$ 의 예측이다. 이것을 이용해 $X_t$ 의 예측값을 구하려면 $X_{t}'$ 를 시간에 따라 적분하면 된다.

요약하면 비정상성을 가진 시계열 $X_t$ 를 ARMA 예측하는 단계는 다음과 같다.

$X_t$ 를 차분한다.
차분한 $X_{t}'$ 을 이용해 ARMA 예측을 한다.
$X_{t}'$ 의 예측값을 시간에 따라 적분하여 $X_t$ 의의 예측값을 구한다.

그리고 이걸 한 번에 수행하는 모델이 있으니 바로 ARIMA(Autoregressive Integrated Moving Average) 모델이다. Integrated가 위에서 말한 차분을 의미한다.

ARIMA Forecasting

앞에서 사용한 ARIMA 패키지를 그대로 사용하고, order = (p, d, q)의 d에 원하는 차분 차수를 입력하면 된다(이전 강의에서는 ARMA 모델을 사용하느라 d=0으로 두었었다).

from statsmodels.tsa.arima.model import ARIMA

model = ARIMA(data, order=(2,1,1))
result = model.fit()
forecast = result.get_forecast(steps=10)
mean_forecast = forecast.predicted_mean