오늘은 인공지능프로그래밍 시간에 배운 선형 회귀 경사하강법에 대해 알아보자.

경사하강법

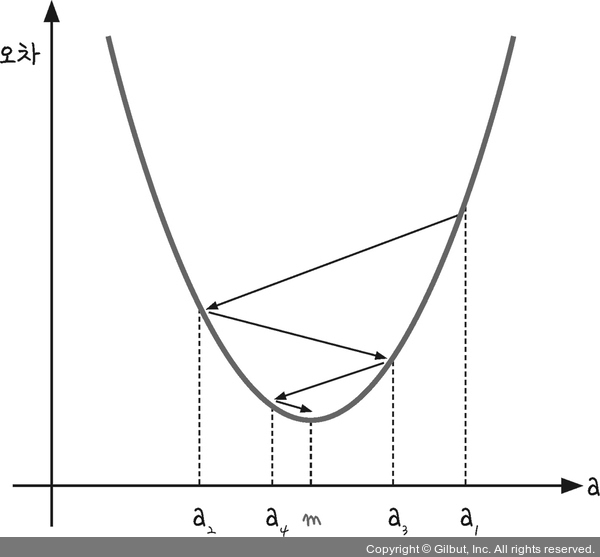
경사 하강법은 이렇게 반복적으로 기울기 a를 변화시켜서 m 값을 찾아내는 방법입니다.
여기서 우리는 학습률(learning rate)이라는 개념을 알 수 있습니다.

학습률을 너무 크게 잡으면?

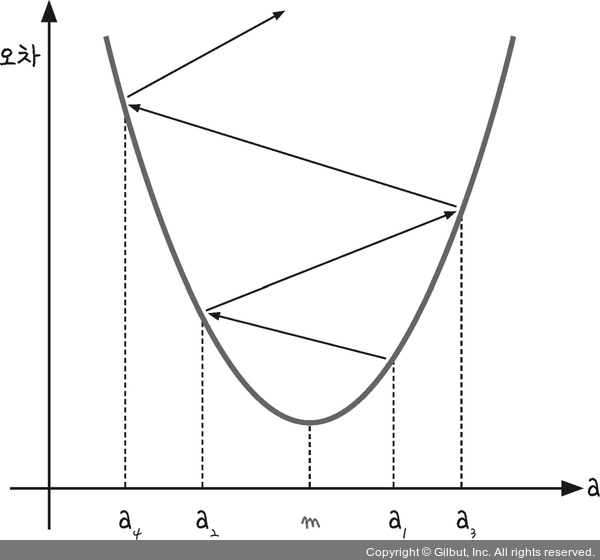
학습률을 너무 크게 잡으면 한 점으로 수렴하지 않고 발산합니다.
그래서 a값이 한점으로 모이지 않고 사진과 같이 위로 솟구칩니다.

학습률을 너무 낮게 잡으면?

학습률을 낮게 잡게 된다면 epoch의 수가 증가하여서 찾는데 시간이 오래걸릴 수 있습니다.

epoch이란?

1 epoch은 순방향 + 역방향 한번을 포함한 의미입니다.

파이썬 코드로 확인해보자

y_pred = a * x + b            # 예측 값을 구하는 식입니다.
error = y - y_pred            # 실제 값과 비교한 오차를 error로 놓습니다.

a_diff = (2/n) * sum(-x * (error))  # 오차 함수를 a로 편미분한 값입니다.
b_diff = (2/n) * sum(-(error))      # 오차 함수를 b로 편미분한 값입니다.

lr = 0.03               # 학습률을 정합니다.
a = a - lr * a_diff     # 학습률을 곱해 기존의 a 값을 업데이트합니다.
b = b - lr * b_diff     # 학습률을 곱해 기존의 b 값을 업데이트합니다.

학습률은 여러 학습률을 적용해보면 정합니다.

import numpy as np
import matplotlib.pyplot as plt

# 공부 시간 X와 성 y의 넘파이 배열을 만듭니다.
x = np.array([2, 4, 6, 8])
y = np.array([81, 93, 91, 97])

# 데이터의 분포를 그래프로 나타냅니다.
plt.scatter(x, y)
plt.show()

# 기울기 a의 값과 절편 b의 값을 초기화합니다.
a = 0
b = 0

# 학습률을 정합니다.
lr = 0.03

# 몇 번 반복될지 설정합니다.
epochs = 2001 

# x 값이 총 몇 개인지 셉니다.
n = len(x)

# 경사 하강법을 시작합니다.
for i in range(epochs):      # 에포크 수만큼 반복합니다.
    y_pred = a * x + b       # 예측 값을 구하는 식입니다.
    error = y - y_pred       # 실제 값과 비교한 오차를 error로 놓습니다.

    a_diff = (2/n) * sum(-x * (error))   # 오차 함수를 a로 편미분한 값입니다.
    b_diff = (2/n) * sum(-(error))       # 오차 함수를 b로 편미분한 값입니다.

    a = a - lr * a_diff   # 학습률을 곱해 기존의 a 값을 업데이트합니다.
    b = b - lr * b_diff   # 학습률을 곱해 기존의 b 값을 업데이트합니다.

    if i % 100 == 0:      # 100번 반복될 때마다 현재의 a 값, b 값을 출력합니다.
        print("epoch=%.f, 기울기=%.04f, 절편=%.04f" % (i, a, b))
        
# 앞서 구한 최종 a 값을 기울기, b 값을 y 절편에 대입해 그래프를 그립니다.
y_pred = a * x + b      

# 그래프를 출력합니다.
plt.scatter(x, y)
plt.plot(x, y_pred,'r')
plt.show()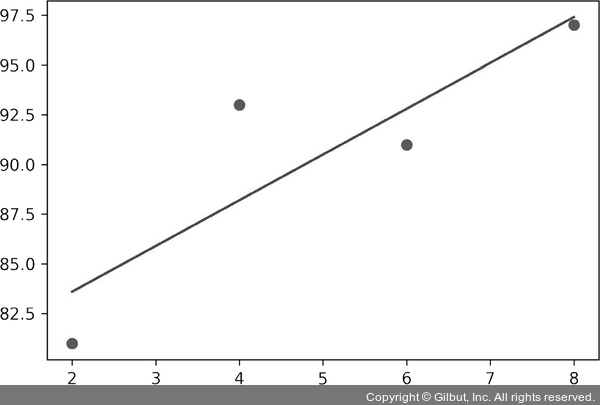![](https://velog.velcdn.com/images/soohyang136/post/cd652ed7-55b6-4732-a533-a72df8644c37/image.png)

실행결과

epoch=0, 기울기=27.8400, 절편=5.4300
epoch=100, 기울기=7.0739, 절편=50.5117
epoch=200, 기울기=4.0960, 절편=68.2822
... (중략) ...
epoch=1900, 기울기=2.3000, 절편=79.0000
epoch=2000, 기울기=2.3000, 절편=79.0000