참고하면 좋은 깃험 : 별 3천개 : https://github.com/life4/textdistance

Levenshtein 거리

(Edit Distance Algorithm)

Python 코드 : ref : https://github.com/life4/textdistance/blob/master/textdistance/algorithms/edit_based.py

seq_A = 'ABCDEFG'+'ABCDEFG'+'ABCDEFG'+'ABCDEFG'
# default

seq_B = 'BCDEFG'+'ABCDEF'+'BCDEFG'+'ABCDEF'
# 첫글자 끝글자 삭제 

seq_C = 'ABCDEF'+'BCDEFG'+'ABCDEF'+'BCDEFG'
# 처음의 끝, 다음의 처음 삭제 

seq_D = 'ABCDEFA'+'GBCDEFG'+'ABCDEFA'+'GBCDEFG'

거리 및 유사도(?) 계산

A B 
 4 
 0.9615384615384616
A C 
 4 
 0.9615384615384616
A D 
 4 
 0.9642857142857143
B C 
 8 
 0.9166666666666666
B D 
 8 
 0.9230769230769231
C D 
 4 
 0.9615384615384616

의도한대로 거리가 나온다. 다만 유사도 관점에서 똑같은 Edit 개수지만
'추가'의 경우, 전체 seqence(string) 길이가 길어지면서 유사도가 높게 나오는 결과가 확인된다.
( 유사도 = 1 - (edit 개수)/전체 길이 )

그러면 르벤스테인 거리를 어떻게 잘 설명할 수 있을까?
컨셉 자체는 간단하다. 3가지 종류의 edit이 있다. 추가/삭제/변경. 최소한의 edit을 통해서 동일한 sequence(string)을 만드는 횟수를 구하는 것이다.

그런데 코드로 구현하려니 막막하다.

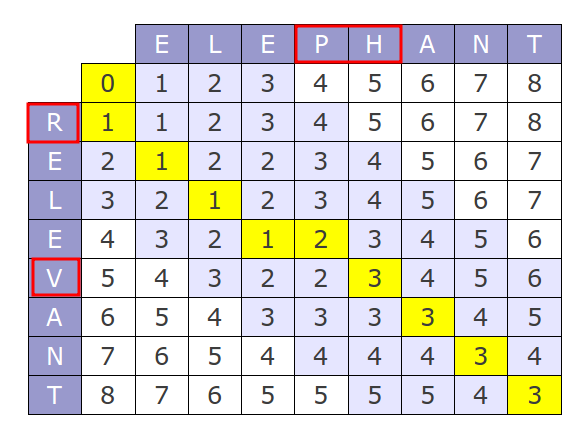
규칙은 다음과 같다.

1) 빨간부분부터 오르쪽으로 하나씩 값을 채워나간다.
2) 빨간 부분의 값을 채울때 다음의 3가지 값중에 가장 작은 값으로 기입한다.

• 초록 : 현재 비교하는 값이 _ 같으면 (초록) +0 __ 값이 다르면 (초록) + 1 -> 0
• 노랑 : 새로운 값을 삽입하는 경우 (노랑) +1 -> 2
• 보라 : 기존 값을 삭제하는 경우 (보라) +1 -> 2
  초록 채택

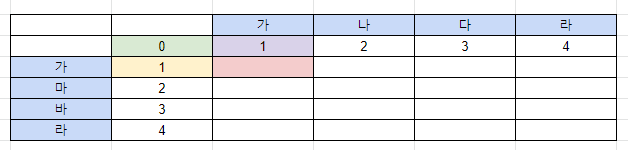
• 초록 : 값이 다르므로 -> 2
• 노랑 : 추가 -> 1
• 보라 : 삭제 -> 3
  노랑 채택

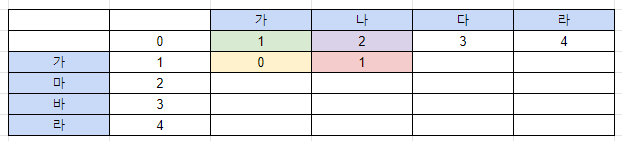
그럼 "가" 행은 0123 이 될 것이다.

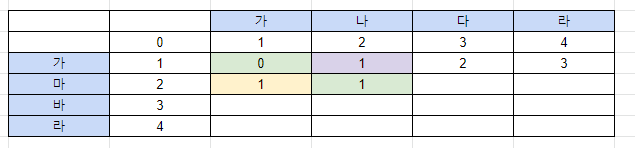
• 초록 : 다르므로 0+1
• 노랑 : 추가 : 2
• 보락 : 삭제 : 2
  초록 채택

마지막 행.열까지 위 과정을 반복한다.

위 과정을 코드로 나타내면 아래와 같다.

class Levenshtein(_Base):

   def _recursive(self, s1: Sequence[T], s2: Sequence[T]) -> int:
       # deletion/insertion
       d = min(
           self(s1[:-1], s2),
           self(s1, s2[:-1]),
       )
       # substitution
       s = self(s1[:-1], s2[:-1])
       return min(d, s) + 1

   def _cycled(self, s1: Sequence[T], s2: Sequence[T]) -> int:
 
       rows = len(s1) + 1
       cols = len(s2) + 1

       cur = range(cols)

       for r in range(1, rows):
           prev, cur = cur, [r] + [0] * (cols - 1)
           for c in range(1, cols):
               deletion = prev[c] + 1
               insertion = cur[c - 1] + 1
               dist = self.test_func(s1[r - 1], s2[c - 1])
               edit = prev[c - 1] + (not dist)
               cur[c] = min(edit, deletion, insertion)
       return cur[-1]

   def __call__(self, s1: Sequence[T], s2: Sequence[T]) -> int:
       s1, s2 = self._get_sequences(s1, s2)

       result = self.quick_answer(s1, s2)
       if result is not None:
           assert isinstance(result, int)
           return result

       return self._cycled(s1, s2)