원제 : Silhouette Method — Better than Elbow Method to find Optimal Clusters
다루게 된 계기 :
https://www.youtube.com/watch?app=desktop&v=xyog_y8gheA
몬스터 때려잡는 매크로 때려잡기 / if(kakao)2022
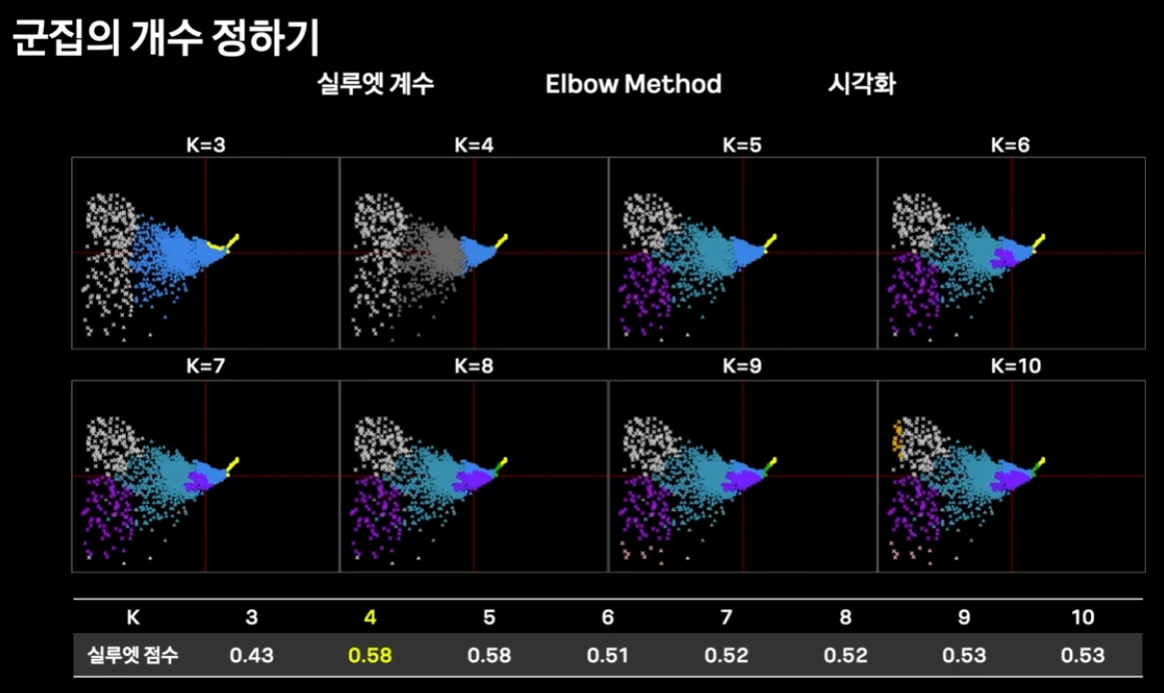
K-means 로 비지도 클러스터링을 정할때
params ( k ) 를 정하기 위해 실루엣 계수를 사용.
정확히 실루엣 계수가 무엇인지? 다뤄보기로 한다.
먼저 실루엣 계수로 param 을 정할때 대조군으로 까일 엘보 방법을 알아보자.
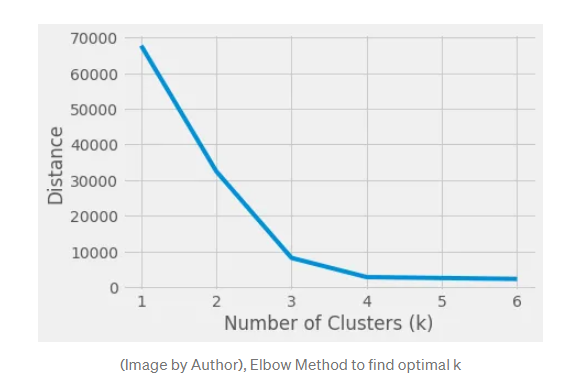
엄청 간단하면서, 나름 직관적이지만, 완벽하지 않은 방법이다.
파라미터를 순회하며 어떤 평가 지표가 초반에 급격히 좋아지다가,
어떤 지점을 지나면서 가성비가 떨어지는 ( 지표가 조금 좋아지는 ) 지
찾는 방식이다.
range_n_clusters = [1, 2, 3, 4, 5, 6]
avg_distance=[]
for n_clusters in range_n_clusters:
clusterer = KMeans(n_clusters=n_clusters, random_state=42).fit(X)
avg_distance.append(clusterer.inertia_)실루엣 계수는 무엇인가?
The silhouette method computes silhouette coefficients of each point that measure how much a point is similar to its own cluster compared to other clusters.
각 점에서 실루엣 계수를 측정하는데, 각 점이 비할당된 여타 클러스터에 비해 할당된 클러스터에 얼마나 비슷한지 측정한다고 한다.
by providing a succinct graphical representation of how well each object has been classified.
그리고 얼마나 잘 할당(분류)되었는지 시각적으로 잘 표현된다고 한다.
The value of the silhouette ranges between [1, -1], where a high value indicates that the object is well matched to its own cluster and poorly matched to neighboring clusters.
실루엣 계수는 -1에서 1의 값을 가지는데 1에 가까울수록 클러스터에 잘 할당되었다는 뜻이다.
If most objects have a high value, then the clustering configuration is appropriate. If many points have a low or negative value, then the clustering configuration may have too many or too few clusters.
클러스터에 할당된 점들이 다 높은 점수를 가진다면, 클러스터링이 잘 된 것으로 해석할 수 있다.
자 그러면 실루엣 계수를 어떻게 계산하는지 알아보자.
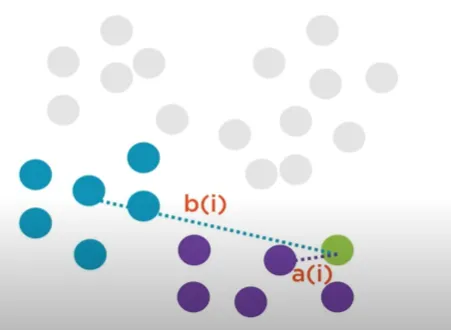
1. Compute a(i): The average distance of that point with all other points in the same clusters.
2. Compute b(i): The average distance of that point with all the points in the closest cluster to its cluster.
3. Compute s(i) — silhouette coefficient or i’th point using below mentioned formula.
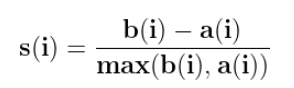
주어진 점이 1000개라면 k-means 클러스터링을 시킬때
k 값을 2에서부터 10까지 순회시킨다고 해보자.
- 그럼 k=2 에서 시작한다. 뭐 어찌됐든 연산이 완료 되어서 모든 점에 대해 클러스터 할당은 되었다.
- 1번 점에서 같은 클러스터에 할당된 1번 아닌 다른 점들과의 거리의 평균을 잰다.
= a(i) - ( 설명이 부실해서 좀 더 찾와바야 할 것 같은데, ) i 에 할당된 클러스터와 가장 가까운 클러스터의 모든 점들의 거리의 평균을 구한다.
= b(i)
( 클러스터간 거리는 클러스터 중심점을 기준이겠지? ) - 위 공식으로 실루엣 계수를 측정한다.
생각해보면 클러스터가 m개, 클러스터 안에 점이 n 개라면
우선 할당된 클러스터안에서 각 점마다 클러스터에 할당된 다른 점 "끼리" 거리를 계산해야 하므로
O(n^2) 계산 복잡도이다. ( 모든 점에 대해서 모든 점끼리 거리를 구해야 하므로. )
scikit-learn 소스코드를 까보자
ef silhouette_score(
X, labels, *, metric="euclidean", sample_size=None, random_state=None, **kwds
):
"""Compute the mean Silhouette Coefficient of all samples.
The Silhouette Coefficient is calculated using the mean intra-cluster
distance (``a``) and the mean nearest-cluster distance (``b``) for each
sample.
평균 기반 가장 가까운 클러스터라고 한다.
여기서 평균 기반이란, 내가 생각한 클러스터 중심점이 맞을까?
The Silhouette Coefficient for a sample is ``(b - a) / max(a,
b)``. To clarify, ``b`` is the distance between a sample and the nearest
cluster that the sample is not a part of.
Note that Silhouette Coefficient is only defined if number of labels
is ``2 <= n_labels <= n_samples - 1``.
This function returns the mean Silhouette Coefficient over all samples.
To obtain the values for each sample, use :func:`silhouette_samples`.
The best value is 1 and the worst value is -1. Values near 0 indicate
overlapping clusters. Negative values generally indicate that a sample has
been assigned to the wrong cluster, as a different cluster is more similar.
Read more in the :ref:`User Guide <silhouette_coefficient>`.
Parameters
----------
def _silhouette_reduce(D_chunk, start, labels, label_freqs):
"""Accumulate silhouette statistics for vertical chunk of X.
Parameters
----------
D_chunk : array-like of shape (n_chunk_samples, n_samples)
Precomputed distances for a chunk.
# ???
# Precomputed distances ?
# 클러스터로 할당된 덩어리 ?
start : int
First index in the chunk.
labels : array-like of shape (n_samples,)
Corresponding cluster labels, encoded as {0, ..., n_clusters-1}.
# 실제 라벨 값
label_freqs : array-like
Distribution of cluster labels in ``labels``.
# 각 라벨로 몇 개의 점들이 있는지 인 것 같다.
# [ 0, 1, 2, 3 ] 라벨
# [ 10, 9, 3, 2 ] 빈도
"""
# accumulate distances from each sample to each cluster
clust_dists = np.zeros((len(D_chunk), len(label_freqs)), dtype=D_chunk.dtype)
# D_chunk 개의 행
# label_freqs ( 클러스터의 개수 ) 개의 열을 0으로 초기화한다.
for i in range(len(D_chunk)):
clust_dists[i] += np.bincount(
labels, weights=D_chunk[i], minlength=len(label_freqs)
)
# np.bincount : 0부터 가장 큰 값까지 각각의 발생 빈도수를 체크합니다.
# A possible use of bincount is to perform sums over variable-size chunks of an array, using the weights keyword.
# w = np.array([0.3, 0.5, 0.2, 0.7, 1., -0.6])
# x = np.array([0, 1, 1, 2, 2, 2])
# np.bincount(x, weights=w)
# array([ 0.3, 0.7, 1.1])
# 그러니까
# 클러스터는 len(D_chunk) 개 있는데, 4개라고 해보자.
# 0 번 클러스터의 경우 [ 0, 1, 2, 3] ,
# intra_index selects intra-cluster distances within clust_dists
intra_index = (np.arange(len(D_chunk)), labels[start : start + len(D_chunk)])
# intra_clust_dists are averaged over cluster size outside this function
intra_clust_dists = clust_dists[intra_index]
# of the remaining distances we normalise and extract the minimum
clust_dists[intra_index] = np.inf
clust_dists /= label_freqs
inter_clust_dists = clust_dists.min(axis=1)
# 이 부분에서 내가 궁금했던 게 나온다.
# clust_dists 가운데에서 가장 작은 값을 리턴한다.
# 즉 모든 클러스터에 대해서 거리를 측정한 다음 그 중에 가장 작은 ( 가까운 )
# 값을 리턴한다.
return intra_clust_dists, inter_clust_dists
def silhouette_samples(X, labels, *, metric="euclidean", **kwds):
X, labels = check_X_y(X, labels, accept_sparse=["csc", "csr"])
# Check for non-zero diagonal entries in precomputed distance matrix
if metric == "precomputed":
error_msg = ValueError(
"The precomputed distance matrix contains non-zero "
"elements on the diagonal. Use np.fill_diagonal(X, 0)."
)
if X.dtype.kind == "f":
atol = np.finfo(X.dtype).eps * 100
if np.any(np.abs(np.diagonal(X)) > atol):
raise ValueError(error_msg)
elif np.any(np.diagonal(X) != 0): # integral dtype
raise ValueError(error_msg)
le = LabelEncoder()
labels = le.fit_transform(labels)
n_samples = len(labels)
label_freqs = np.bincount(labels)
check_number_of_labels(len(le.classes_), n_samples)
kwds["metric"] = metric
reduce_func = functools.partial(
_silhouette_reduce, labels=labels, label_freqs=label_freqs
)
results = zip(*pairwise_distances_chunked(X, reduce_func=reduce_func, **kwds))
intra_clust_dists, inter_clust_dists = results
intra_clust_dists = np.concatenate(intra_clust_dists)
inter_clust_dists = np.concatenate(inter_clust_dists)
denom = (label_freqs - 1).take(labels, mode="clip")
with np.errstate(divide="ignore", invalid="ignore"):
intra_clust_dists /= denom
sil_samples = inter_clust_dists - intra_clust_dists
with np.errstate(divide="ignore", invalid="ignore"):
sil_samples /= np.maximum(intra_clust_dists, inter_clust_dists)
# nan values are for clusters of size 1, and should be 0
return np.nan_to_num(sil_samples)
