출처 : (마할라노비스 거리 , 공돌이의 수학노트)
- https://angeloyeo.github.io/2022/09/28/Mahalanobis_distance.html
- 마할라노비스 거리에 대한 전반적인 설명

출처 : [데이터분석 정리] Mahalanobis거리와 MCD 개인적 정리
- https://godongyoung.github.io/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D/2019/02/11/Mahalanobis-and-MCD.html
- 마할라노비스 거리랑 유사한건데, 좀 더 이상치에 Robust한 거리 개념이 MCD 이다.

출처 : ([영상처리] 이미지매칭(1) - 마할라노비스 거리 & 화이트닝 변환)
- https://kimyo-s.tistory.com/46 
- 화이트닝 변환을 하면 유클리드 거리 = 마할라노비스 거리

출처 : [선형대수] 내적(inner product) 의미
- https://losskatsu.github.io/linear-algebra/innerproduct/#

마할라노비스 거리란?

• 수식을 보면 이렇게 생겼다.
  
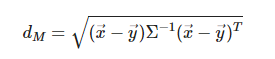
• 컨셉적으로 생각하면 확률 분포를 통해 등고선을 그릴 수 있고, 평균으로부터 몇번째 등고선에 있는지로 거리를 계산하는 것이다.
  

이젠 저 컨셉이 어떻게 저런 이상한 수식으로 표현될 수 있는지 알아보자.

• 우선 두 점 사이의 거리를 어떻게 표현하는가?
  - (선형대수학) 두 벡터(좌표)의 내적으로 거리를 표현한다.
  
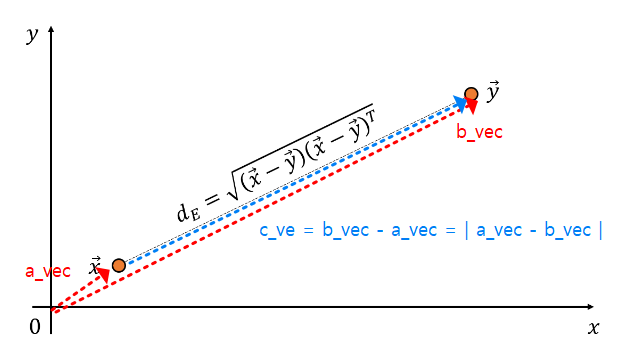
• 위 이미지에서 c_vec = b_vec - a_vec 임을 알 수 있다.
• c_vec 의 길이는 root of (c_vec 의 제곱) 입니다.
• c_vec 의 길이는 root of (b_vec - a_vec 의 제곱) 입니다.
• 어떤 벡터의 제곱은 vec * vec_T 라고 볼 수 있습니다.

변수별로 정규화 한 다음

• 출처 : https://blog.naver.com/sw4r/221378314681